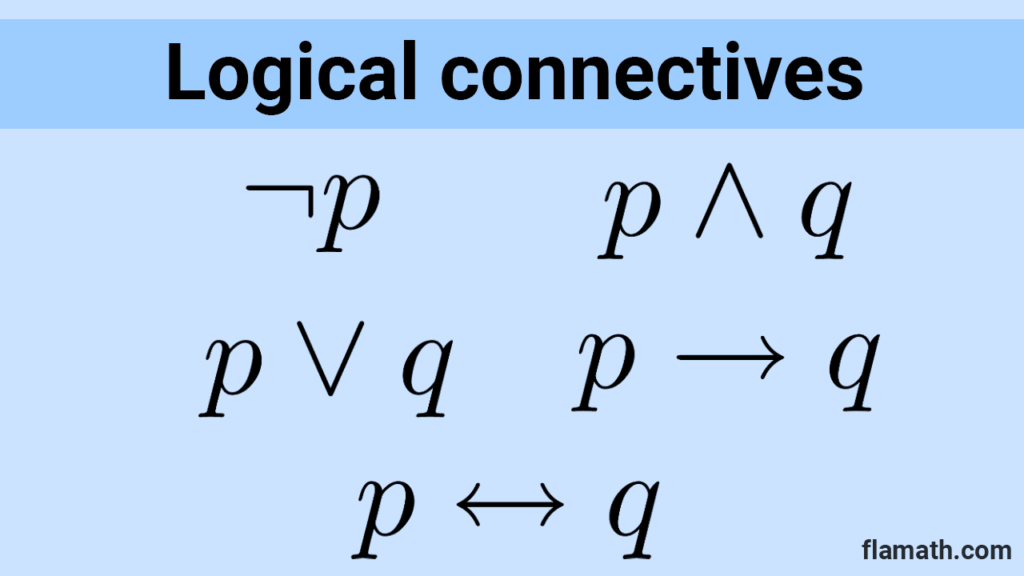
Logical connectives
In this article we explain what are logical connectives in propositional calculus. We will see how many types there are and the complete list of them with their symbols and truth tables.
Table of Contents
What is a logic connective?
A connector or logical connective is an element of language that allows us to construct new statements from existing ones. We can also consider them as logical operators, since we perform certain operations between propositions to construct new ones. The propositions obtained are compounds and can also be combined through connectives to form others.
List of logic connectives
In propositional logic, six logical operators are used: negation, conjunction, inclusive disjunction, exclusive disjunction, conditional, and biconditional.
| Symbol | Logical Connective | Meaning |
|---|---|---|
| ¬ (also ~) | Negation | not p it is not true that p it does not happen that p it is false that p |
| *\land* | Conjunction | p and q p although q p but q p however q p nevertheless q p despite q |
| *\lor* | Disjunction | p or q or both either p or q |
| *⊻* | Exclusive Disjunction (or symmetric difference) | p or q, but not both either p or q, but not both |
| *→* | Conditional (or implication) | if p, then q only if p, then q p is sufficient for q q is necessary for p not p unless q |
| *↔* | Biconditional (or double implication) | p if and only if q p sufficient and necessary for q |
Negation
Negation of proposition p is the proposition ¬p (read as "not p"). The negator has the same meaning as the ordinary language particle "no." When we negate a statement, our intention is to say that the statement is false.
- If a proposition is true, its negation is false.
- If a proposition is false, its negation is true.
We represent the truth conditions of this connector using a table. The initial column lists the possible truth values of a particular statement p. The next column indicates the truth values corresponding to the negation of the statement.
| p | ¬p |
|---|---|
| T | F |
| F | T |
Example 1:
p: "The Moon orbits the Earth"
¬p: "The Moon does not orbit the Earth"
V(p)=T
V(¬p)=F
Example 2:
q: "Fish can breathe out of water"
¬q: "It is not true that fish can breathe out of water"
V(q)=F
V(¬q)=T
The negation of a proposition can be read in the following ways:
- not p.
- it's not true that p.
- it doesn't happen that p.
- it's false that p.
Conjunction
Conjunction of propositions p and q is the proposition p∧q (read as "p and q"). The meaning of the conjunction is identical to that of "and" in ordinary language. A conjunction is true when its components are true; it is false in any other case.
We represent the truth conditions using a table similar to the previous one. In the first two columns, the four possible combinations of truth and falsehood of propositions p and q are listed in order. The third column indicates the truth values corresponding to each case.
| p | q | p ∧ q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
Example 1:
p: "The piano is a musical instrument"
q: "2 is an even number"
p∧q: "The piano is a musical instrument and 2 is an even number"
V(p∧q)=T because both propositions are true.
Example 2:
r: "The color of the sky is red"
s: "2+2 is 4"
r∧s: "The sky is red and 2+2 is 4"
V(r∧s)=F because only the second proposition is true, the first one is not.
The conjunction of two propositions can be read in the following ways:
- p and q.
- p although q.
- p but q.
- p however q.
- p nevertheless q.
- p despite q.
Inclusive disjunction
Disjunction of p and q is the proposition p∨q (read as "p or q"). The disjunctive can be partially considered as a formal language translation of the ordinary language particle "or." The disjunction of two propositions is true when at least one of these propositions is true (and when both are); it is false when both are false.
| p | q | p ∨ q |
|---|---|---|
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
It is easy to see that the truth conditions of disjunction are the "counterpart" of the truth conditions of conjunction. Also, the symbol for disjunction (∨) is the inverted image of the conjunctive (ʌ).
To prove the truth of a conjunction, it is necessary to prove the truth of all its members; to prove the truth of disjunction, it is sufficient to prove the truth of one. Conversely, the same applies to falsehood: the falsehood of a conjunction is established by proving the falsehood of one of its members, while the falsehood of disjunction requires proving the falsehood of all.
Example 1:
p: "The Sun is a planet"
q: "Earth is a planet"
p∨q: "The Sun is a planet or Earth is a planet"
V(p∨q)=T because the second proposition is true.
Example 2:
r: "Fish can fly"
s: "3 is an even number"
r∨s: "Fish can fly or 3 is an even number"
V(r∨s)=F because both propositions are false.
The inclusive disjunction of two propositions can be read in the following ways:
- p or q or both.
- either p or q or both.
Exclusive disjunction
Exclusive Disjunction of p and q is the proposition p⊻q (read as "p or q, but not both"). It is true when only one of the two propositions is true; it is false if both are false or if both are true simultaneously.
| p | q | p ⊻ q |
|---|---|---|
| T | T | F |
| T | F | T |
| F | T | T |
| F | F | F |
This connective can be considered as the formal language translation of the particle "or" in an exclusive sense, that is when you want to indicate that one thing happens or another, but not both at the same time. It mainly differs from the other disjunction by this.
Example 1:
p: "4 is an even number"
q: "6 is an even number"
p⊻q: "4 is an even number or 6 is an even number, but not both"
V(p⊻q)=F because both propositions are true simultaneously.
Example 2:
r: "Earth is flat"
s: "Earth is spherical"
r⊻s: "Earth is flat or is spherical, but not both"
V(r⊻s)=T because only the second proposition is true.
The exclusive disjunction of two propositions can be read in the following ways:
- p or q, but not both.
- either p or q, but not both.
Conditional (or implication)
Implication of propositions p and q is the proposition p → q (read as "if p, then q" or "p implies q"). The implication can be considered as a partial formalization of the ordinary language particle "if..., then...". The expression preceding the symbol is called the antecedent (p), and the one following it is the consequent (q).
An implication is true when its antecedent is false or when its consequent is true; it is false when its antecedent is true, and its consequent is false.
| p | q | p → q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
The definition just given may seem to clash with the ordinary use of the particle "if..., then...", which usually conveys the idea that there is some kind of internal relationship between the content of the antecedent and the consequent.
This can be clarified by understanding that the logic of connectors is based solely on the truth value of propositions and does not take into account their content.
Example 1:
p: "2 is an even number"
q: "3 is an even number"
p→q: "If 2 is an even number, then 3 is an even number"
V(p→q)=F because the antecedent is true, and the consequent is false.
Example 2:
r: "Juan passes the exam"
s: "Juan's mother will give him a gift"
r→s: "If Juan passes the exam, his mother will give him a gift"
If we assume that Juan passed his exam but his mother didn't give him the gift, then V(r→s)=F because the antecedent is true, and the consequent is false. If Juan passed, and his mother did give him the gift, then V(r→s)=T, because both the antecedent and consequent are true.
If we assume that Juan didn't pass his exam, no matter what happens with the consequent, V(r→s)=T. His mother can decide whether to give him the gift or not.
The implication of two propositions can be read in the following ways:
- if p, then q.
- only if p, then q.
- p is sufficient for q.
- q is necessary for p.
- not p unless q.
Implication is widely used in the statement of theorems and mathematical properties, so it is interesting to know the implications associated with p → q. Then, given the implication p → q
q→p is the reciprocal implication, where we permute the propositions.
¬p →¬q is the contrary implication, where we negate both propositions without changing their order.
¬q→¬p is the contrapositive implication, where we permute and negate both propositions.
It can be demonstrated that any implication is equivalent to its contrapositive.
Example:
p: "It's raining"
q: "The courtyard is wet"
p→q: "If it's raining, then the courtyard is wet"
Reciprocal: q→p: "If the courtyard is wet, then it's raining"
Contrary: ¬p→¬q: "If it's not raining, then the courtyard is not wet"
Contrapositive: ¬q→¬p: "If the courtyard is not wet, then it's not raining"
Notice that the reciprocal and contrary implications are not equivalent to the original, as the courtyard could be wet even when it's not raining (someone could pour water). In contrast, if the courtyard is not wet, we can be sure it's not raining.
Biconditional (or double implication)
Biconditional of propositions p and q is the proposition p ↔ q (read as "p if and only if q"). This connective can be considered as the formal language translation of the particle "when and only when" and also "is equivalent to." It is used in establishing definitions of equivalence and expressing necessary and sufficient conditions.
A biconditional is true when both of its components have the same truth value, meaning when both are true or both are false; and it is false otherwise, meaning when one of them is true and the other is false.
| p | q | p ↔ q |
|---|---|---|
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
Example:
p: "A triangle is equilateral"
q: "The three sides of a triangle are equal"
p↔q: "A triangle is equilateral if and only if its three sides are equal"
V(p↔q)=T
The double implication of two propositions can be read in the following ways:
- p if and only if q.
- p sufficient and necessary for q.
- p is equivalent to q.
Hierarchy of logical connectives
When using logical symbols, we establish a hierarchy among them to avoid excessive use of parentheses. The convention indicates the following order:
- ↔
- →
- ʌ v
- ¬
Examples:
*¬p→q↔r\land s→t* should be understood as *(¬p → q) ↔ [(r \land s) → t]*
*p↔¬q\lor r* is *p↔(¬q\lor r)*
*¬p\land q* is *(¬p)\land q*
Notice that negation only affects the immediate proposition, unless parentheses modify it, for example, *¬(p\land q).*
Practice exercises
Exercise: given the propositions:
p: "The sky is cloudy".
q: "A triangle has three sides".
r: "It's raining".
s: "The bell is ringing".
t: "The dog is barking".
Formulate the following compound propositions:
- *¬p∧q*
- *s→¬(t∨r)*
- *p⊻s→t*
- *q↔¬t*
- *¬(r∧s)*
- *t→s*
- *p→q∧r*
Solutions:
- *¬p∧q:* "The sky is not cloudy and a triangle has three sides".
- *s→¬(t∨r):* "If the bell is ringing, then it's not true that the dog is barking or it's raining".
- *p⊻s→t:* "If the sky is cloudy or the bell is ringing (but not both), then the dog is barking".
- *q↔¬t:* "A triangle has three sides if and only if the dog is not barking".
- *¬(r∧s):* "It's false that it's raining and the bell is ringing".
- *t→s:* "If the dog is barking, then the bell is ringing".
- *p→q∧r:* "If the sky is cloudy, then a triangle has three sides and it's raining".
FAQs
What are logical connectives in mathematics?
In discrete mathematics, a logical connective is an element that allows connecting simple or compound propositions to create new propositions.
How many logical connectives are there in mathematics?
In propositional logic we work with six logical connective: negation, conjunction, inclusive disjunction, exclusive disjunction, conditional and biconditional.

Other articles that may interest you