
Natural numbers
In this article we explain the set of natural numbers. We start from its concept and definition and we will see its representation form, properties, the operations that can be performed and the restrictions that they have.
Table of Contents
What are natural numbers?
Natural numbers are those we use for counting and ordering: 1, 2, 3, 4, 5, etc. All natural numbers are positive integers, that is, fractions and negatives are not natural numbers.
We generally use these numbers to count quantities, for example: the alphabet has 27 letters, the rainbow has 7 colors, etc. We also use them to indicate order, for example, in a race of ten participants, we order them according to their arrival time at the finish line from first place to tenth place.
In addition to those mentioned at the beginning, some examples of natural numbers are: 10, 15, 50, 92, 103, 245, 444, 13, 1000, 4560. If we add 1 to a natural number, we get another natural number. The following are examples of numbers that are not natural: -70, 2/3; 6.5; π, √2.
Set of natural numbers
The set of natural numbers is designated by the letter N:
*\mathbb{N}=\{1,2,3,4,5,...\}*
Natural numbers are the most basic set of numbers from which others can be constructed: integers, rationals, reals, complex numbers. Natural numbers are a subset of integers, which in turn are a subset of rationals, and this of real numbers. So, all natural numbers are integers, rationals, and reals.
Depending on the use intended, zero may or may not be considered a natural number. This number serves the purpose of indicating the absence of objects to count or order. Additionally, as we will see shortly, if zero is accepted as a natural number, it allows the sum to have a neutral element. The set of naturals with zero is usually called whole numbers.
When explicitly indicating that zero is considered a natural number, the zero subscript is placed on the set symbol:
*\mathbb{N}_0=\{0,1,2,3,4,5,...\}*
Characteristics and properties
Some characteristics and properties of natural numbers are:
- The set of natural numbers is ordered and infinite, which means that new natural numbers can always be found, and two different numbers can be compared to determine which one is smaller (or larger).
- The set of natural numbers has a first element, which is 1 (or 0, if considered natural); this number is the smallest of all natural numbers. Due to being an infinite set, there is no largest natural number.
- Every natural number has a successor. A natural number and its successor are called consecutive. The successor of a natural number can be obtained by adding 1.
- Every natural number, except the first one, has a predecessor. The predecessor of a natural number can be obtained by subtracting 1.
- Between two natural numbers, there is always a finite number of natural numbers. Hence, it is said to be a discrete set, or not dense.
- There are no natural numbers between a natural number and its successor.
- Natural numbers can be added, subtracted, multiplied, and divided, with some restrictions.
Representation on the number line
Natural numbers can be represented using the number line. Each number is placed with the same spacing between them:
As the set of natural numbers is unlimited, the line extends infinitely to the right, as indicated by the arrow.
Operations between natural numbers
We can define operations such as addition, subtraction, multiplication, division, exponentiation, and root extraction between natural numbers.
Let *a*, *b*, and *c* be natural numbers. The addition and multiplication of natural numbers fulfill the following properties:
Closure property: the sum and product of two natural numbers is another natural number.
*a+b~* is a natural number
*a\cdot b~* is a natural number
Associative property: the order in which numbers are grouped does not alter the final result.
*(a+b)+c=a+(b+c)*
*(a\cdot b)\cdot c=a\cdot (b\cdot c)*
Commutative property: the order in which numbers are placed in the operation does not alter the result.
*a+b=b+a*
*a\cdot b=b\cdot a*
Neutral element: the number 0, when added to any other natural number, does not alter its value: *a+0=a.* The number 1, when multiplied by another natural number, does not alter its value: *a\cdot 1=a.*
It is considered that zero is a natural number, as this number has the property of being the neutral element of addition. If 0 is not considered natural, there is only a neutral element for multiplication.
Distributive property: multiplication distributes over addition.
*a\cdot (b+c)=ab+ac*
As mentioned, natural numbers can be added and multiplied, and the result of these operations is also a natural number. However, the same does not apply to subtraction and division:
- The subtraction of two natural numbers is a natural number only if the minuend is greater than the subtrahend. Otherwise, the result is not natural. For example: the result of *2-3* is not a natural number.
- The division of two natural numbers is natural only when the dividend is a multiple of the divisor, in other words, when the division is exact. For example, the result of *7:4* is not a natural number.
Limitations of natural numbers
The main limitation of natural numbers is that they are unable to represent negative or fractional magnitudes. In other words, they cannot be used to measure quantities that are "less than nothing" or are non-whole parts of a whole. For example:
- A natural number cannot be used to represent a debt, loss, or temperature below zero.
- A natural number cannot represent quantities like half an apple, a third of a pizza, or half a meter.
Operationally, these limitations are seen in subtraction and division. It is not possible to solve in the set of natural numbers the operations *a-b* when *a<b* or *a:b* when *a* is not a multiple of *b*. There are also no symmetric elements for addition and multiplication.
To overcome the limitations of natural numbers, other numerical sets were created, such as integers, rational numbers, and real numbers.
FAQs
What are natural numbers and what are they used for?
Natural numbers are those from the infinite sequence 1, 2, 3, 4,... and are used to count quantities and order elements.
Why are they called natural numbers?
Natural numbers are called so because they represent natural quantities and counts of elements that are intuitively found in nature. Since ancient times, humans have used natural numbers to count objects, people, animals, and other quantifiable entities that naturally exist in the world around us.
With what letter are natural numbers represented?
Natural numbers are represented by the uppercase letter N. If zero is considered a natural number, a subscript with that number is added to the same letter: N0.
What are the properties of natural numbers?
The field of natural numbers fulfills the following properties.
1. It is an infinite and ordered set.
2. It has a first element, but it does not have a last element.
3. Every natural number has a successor.
4. Every natural number, except the first one, has a predecessor.
5. Between two natural numbers, there is a finite number of natural numbers.
6. There is no natural number between a natural number and its successor.
Is zero a natural number?
Depending on the use intended, zero is or is not a natural number. For example, if it is necessary to count the elements of a set, zero is included in the natural numbers, as sets can exist without elements. The set of naturals with zero is called the whole numbers.
Why are natural numbers not dense?
Natural numbers are not dense because between any pair of natural numbers, there is always a finite number of intermediate natural numbers, regardless of how large the numbers in question are.
What relationship do natural numbers have with other numerical sets?
Natural numbers are the basis of broader numerical sets, such as integers, rationals, reals, and complexes. Each broader numerical set includes natural numbers and adds new classes of numbers to cover a wider range of values.
What is the first natural number?
Natural numbers start at the number 1. If 0 is considered to be a natural number, then 0 is the first natural number.
What is the largest natural number?
There is no natural number that is greater than all, as natural numbers extend infinitely in the positive direction.
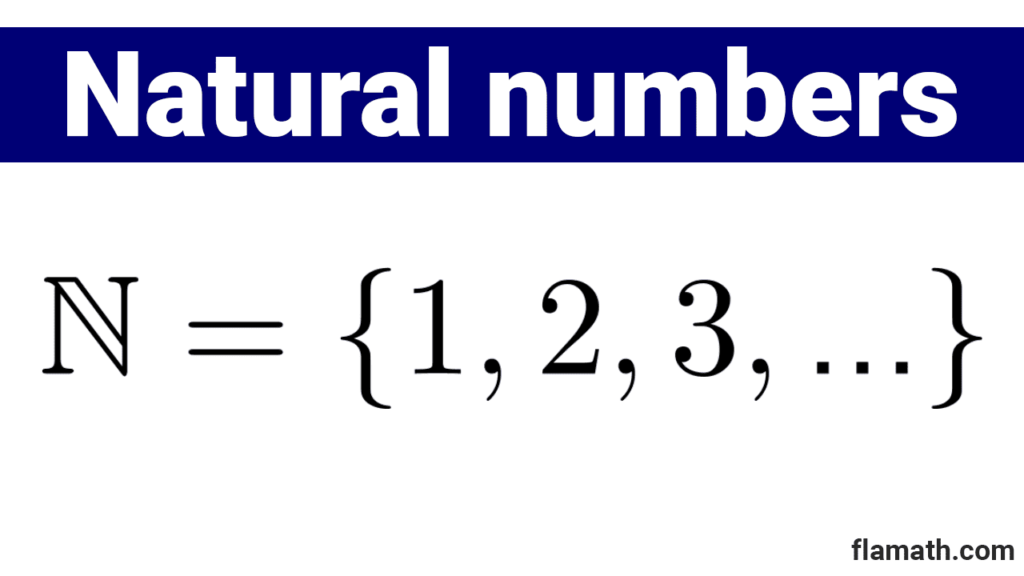


Other articles that may interest you