
Number sets
Number sets are a way of classifying different types of numbers according to their properties and characteristics. In this section we are going to review the main numerical sets and also the ways of writing them, as well as some examples and practical exercises to understand them better.
Table of Contents
What are numeric sets?
Numeric sets are groupings or collections of numbers organized according to their common mathematical properties. Each set has its own definition and properties that distinguish it from others, allowing for a variety of mathematical situations and problems to be addressed precisely and effectively.
Numeric sets form the basis of arithmetic and mathematical analysis and are essential for understanding and solving a wide range of problems in mathematics and other scientific disciplines such as physics, engineering, economics, statistics, and programming, among others.
How many numeric sets are there?
There are six fundamental numeric sets, namely: natural numbers (N), integers (Z), rationals (Q), irrationals (I), real numbers (R), and complex numbers (C). In the historical development of mathematics, to overcome the limitations of a numeric set, other classes of numbers were successively introduced to solve new problems.
You can learn about the definition and characteristics of each one by visiting their respective articles:
Numeric sets diagram
Numeric sets can be schematized as follows.
Natural numbers
Natural numbers are the elements of the sequence *1, 2, 3, 4,…* and were the first used by ancient civilizations to count objects and represent quantities. Each of them has a successor greater by one unit, for example, the successor of *12* is *12+1=13.*
The set of natural numbers is symbolized by the letter N:
$$ \mathbb{N}=\{1, 2, 3, 4, 5, …\} $$
Natural numbers are used to count objects and represent discrete quantities; for example, they are used to count the number of people in a meeting or the total number of elements in a set. They also allow for establishing a sequential order; for example, they can be used to enumerate positions in a competition or stages in a process.
The number zero is sometimes considered as a natural number, as it is necessary to mark the absence of elements to count. For example, to express that there are no students in a classroom, it could be said that there are zero students. The set of naturals with zero is usually called the whole numbers. If we need to include zero in natural numbers, we place a subscript on the set symbol:
$$ \mathbb{N}_0=\{0, 1, 2, 3, 4, 5, …\} $$
Some examples of natural numbers are: 66, 210, 15, 50, 92, 103, 245. All natural numbers are positive numbers (non-negative if zero is included).
In this set, we can define arithmetic operations such as addition, subtraction, multiplication, division, exponentiation, and root extraction. We will consider zero as a natural number. We will see the properties of these operations below.
The most important properties of the set of natural numbers are:
- It is infinite and ordered.
- It has a first element, but it does not have a last element.
- Every natural number has a successor.
- Between any two natural numbers, there is always a finite number of natural numbers.
Limitations of natural numbers
The set of natural numbers is limited in the sense that some operations cannot be performed taking any two natural numbers, as the result may not be a natural number. For example:
- When subtracting two natural numbers, the minuend cannot be smaller than the subtrahend.
- Exact division cannot be performed if the dividend is not a multiple of the divisor.
- The nth root of a natural number cannot be extracted if it is not also the nth power of a natural number.
Division by zero is also prohibited, but this is not specific to natural numbers, it occurs in all numeric sets.
Integers
There are everyday expressions that cannot be indicated with natural numbers. For this, it is necessary to use negative numbers:
- When talking about temperatures below zero. For example, 5 °C below zero is expressed as -5 °C.
- When referring to debts. For example, if we owe $500, we say that our balance is -$500.
- When referring to the floors of a building. Example: the basement is the floor -1.
Integers arise as a solution to the limitation of natural numbers regarding subtraction. Introducing negative numbers *-1, -2, -3,…* allows performing the subtraction operation *a-b* even when *a* is less than *b.* We integrate negative numbers and zero into naturals to form a new numeric set.
The set of integers is represented by the letter Z and is formed by the natural numbers (1, 2, 3, 4, ...), the negative numbers (-1, -2, -3, -4, ...), and zero (0).
$$\mathbb{Z}=\{…, -4, -3, -2, -1, 0, 1, 2, 3, 4, … \}$$
Some examples of integers are: -40, 2, 0, 27, -34, 18.

Operations with integers are defined so that whenever dealing with positive numbers, the definitions and properties corresponding to natural numbers are preserved. Thus, to add two integers, if they both have the same sign, this sign is placed, and the sum of the corresponding natural numbers is performed, and if they have different signs, the sign of the greater one is placed first, and they are subtracted. For the product and quotient, the rule of signs is adopted: factors of the same sign give a positive product and of different signs a negative product.
The most important properties of the set of integers are:
- It is infinite and ordered.
- It has no first or last element.
- Every integer has a successor.
- Between two integers, there is always a finite number of integers.
Limitations of integers
If integers are used for addition, subtraction, or multiplication, integers are always obtained. However, we still maintain the limitations of natural numbers and a new one arises:
- Exact division cannot be performed if the dividend is not a multiple of the divisor.
- The nth root of an integer cannot be extracted if it is not also the nth power of an integer. Also, roots with an even index of negative numbers do not exist.
Subsets of integers
From the set of integers, we can define a series of subsets:
- Positive integers *\mathbb{Z}^+:* these are all natural integers. *\mathbb{Z}^+=\{1,2,3,4,...\}.*
- Negative integers *\mathbb{Z}^-:* these are all negative numbers, opposites of the natural ones. *\mathbb{Z}^-=\{-1,-2,-3,-4,...\}.*
- Non-negative integers *\mathbb{Z}^{+}_0:* these are all positive integers plus zero. *\mathbb{Z}^{+}_0=\{0,1,2,3,4,5,...\}.*
- Non-positive integers *\mathbb{Z}^{-}_0:* these are all negative integers plus zero. *\mathbb{Z}^{+}_0=\{0,-1,-2,-3,-4,-5,...\}.*
- Integers without zero: *\mathbb{Z}^{*}=\{-2,-1,1,2,3,...\}*
Note: the notations of the subsets are maintained in the following numeric sets up to real numbers. To indicate positive numbers, a + exponent is placed on the set symbol; to indicate negative numbers, a - exponent is placed; to indicate the inclusion of zero, 0 is placed as a subscript; to indicate the absence of zero, an asterisk is placed as an exponent.
Rational numbers
The introduction of fractional numbers *a/b* allows exact quotients *a÷b* between integers, even in cases where *a* is not a multiple of *b.* The integer *a* is called the numerator, and the integer *b,* which cannot be 0, is called the denominator.
Integers and fractions together form the set of rational numbers symbolized by the letter Q:
$$ \mathbb{Q}=\left\{\frac{a}{b}~\text{such that a and b are integers and b is not zero}\right\} $$
Fractional numbers serve, among other things, to represent parts of a total quantity, for example, 1/4 of a cake means a piece of a cake divided into 4 equal parts. Also, fractions are essential for expressing proportions and rates, such as interest rates, growth percentages, and relationships between quantities.
Some examples of rational numbers are: 1/2, 3/4, -5/3, 27/7.
The most important properties of the set of rational numbers are as follows:
- It is infinite and ordered.
- It has no first or last element.
- Between two rational numbers, there are infinitely many rational numbers.
An integer can be written as a fraction with a denominator of 1, allowing us to say that every integer is rational. Before defining operations between fractions, we will emphasize the property of equality:
*\dfrac{a}{b}=\dfrac{c}{d}* if and only if *ad=bc*
This relationship tells us that two fractional numbers are equal if their cross products are equal. Two fractions that meet this condition are called equivalent fractions. For example, *1/2* is equivalent to *6/12,* because *1\cdot 12=2\cdot 6.*
To obtain a fraction equivalent to a given fraction, we can multiply the numerator and denominator by the same integer. We can also divide the numerator and denominator by the same integer, provided that it is a divisor of both.
Operations with rational numbers
*\dfrac{a}{b}+\dfrac{c}{d}=\dfrac{ad+bc}{bd}*
*\dfrac{a}{b}-\dfrac{c}{d}=\dfrac{ad-bc}{bd}*
*\dfrac{a}{b}\cdot \dfrac{c}{d}=\dfrac{a\cdot c}{b\cdot d}*
*\dfrac{a}{b}:\dfrac{c}{d}=\dfrac{a}{b}\cdot \dfrac{d}{c}=\dfrac{a\cdot d}{b\cdot c}*
*\left(\dfrac{a}{b}\right)^n=\dfrac{a^n}{b^n}*
*\sqrt[n]{\dfrac{a}{b}}=\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}}*
Limitations of rational numbers
When performing additions, subtractions, products, and divisions (except division by zero) among rational numbers, a rational number is always obtained. However, we still have an important limitation:
- The nth root of a rational number cannot be extracted if it is not itself the nth power of a rational number. Also, even roots of negative numbers have no solution.
Subsets of rational numbers
Just like with integers, we can define a series of subsets that are frequently used.
- Positive rationals: *\mathbb{Q}^+=\left\{\dfrac{a}{b}~\text{such that}~\dfrac{a}{b}>0\right\}*
- Negative rationals: *\mathbb{Q}^-=\left\{\dfrac{a}{b}~\text{such that}~\dfrac{a}{b}<0\right\}*
- Non-negative rationals: *\mathbb{Q}^+_0=\left\{\dfrac{a}{b}~\text{such that}~\dfrac{a}{b}≥0\right\}*
- Non-positive rationals: *\mathbb{Q}^-_0=\left\{\dfrac{a}{b}~\text{such that}~\dfrac{a}{b}≤0\right\}*
- Rationals without zero: *\mathbb{Q}^{*}=\left\{\dfrac{a}{b}~\text{such that}~\dfrac{a}{b}≠0\right\}*
Decimal numbers
Decimal numbers do not constitute a set in themselves but are a way of expressing numbers. Sometimes rational numbers are represented as decimals. For example, the numbers *3/4*, *5/2*, *-2/3*, and *7/66* can be represented as decimals simply by performing division:
*\dfrac{3}{4}= 0.75*
*\dfrac{5}{2} = 2.5*
*-\dfrac{2}{3}=-0.6666… = -0. \overline{6}*
*\dfrac{7}{66}=0.1060606…=0.1 \overline{0} \overline{6}*
We observe that the decimal representation of *3/4* and *5/2* ends or terminates, these are called exact decimals. The decimal representation of the other two numbers does not end, but a repeating pattern is seen. For *-2/3*, 6 repeats indefinitely, as indicated by the bar over it; for *7/66*, the block 06 repeats indefinitely, as indicated by the bar over 06. These latter two are called repeating decimals.
It is possible to demonstrate that every rational number can be represented by a decimal that ends or does not end and has a block of repeating digits, and vice versa.
Irrational numbers
There are numbers whose decimal expression does not fall into either of the two categories mentioned earlier, i.e., they are neither exact nor repeating decimals, but rather have infinite decimal places and these do not follow any pattern.
These numbers cannot be written as fractions; therefore, they are not rational but rather another type of numbers called irrational. In other words, irrational numbers are those that cannot be written as a fraction *a/b*, where a, b are integers and b is not zero.
The set of irrational numbers is symbolized by the letter I:
*\mathbb{I}=\{x~\text{such that x cannot be written as a fraction}\}*
Irrational numbers arise naturally. For example, if we consider an isosceles right triangle whose legs have length 1, the hypotenuse measures *\sqrt{2}*, an irrational number.
Some famous irrational numbers are:
- *π=3.14159265…* which represents the ratio of the circumference to its diameter.
- *e=2.71828182…* the base of natural logarithms.
- *ϕ=1.61803399…* the golden ratio.
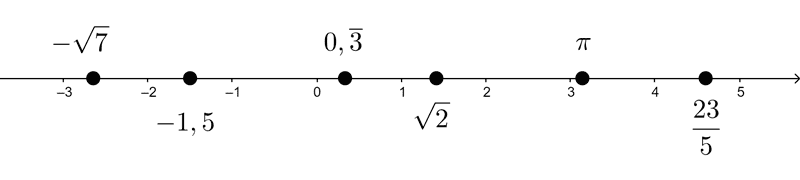
Real numbers
So far, we have two major groups of numbers: rationals and irrationals. The former can be written as a fraction and include integers and naturals; the latter group contains all numbers that cannot be written as a fraction.
By combining rational and irrational numbers into one, we form the set of real numbers, symbolized by the letter R:
*\mathbb{R}=\mathbb{Q}\cup \mathbb{I}*
Real numbers allow solving roots that cannot be solved with rational numbers, for example: *\sqrt{2},~~\sqrt{\dfrac{5}{3}},~~\sqrt[3]{7}* are real numbers.
The most important properties of the set of real numbers are:
- It is infinite and ordered.
- It has no first or last element.
- Between two real numbers, there is an infinite number of real numbers.
If a, b, and c are real numbers, addition has the following properties.
- Commutative property: *a+b=b+a*
- Associative property: *a+(b+c)=(a+b)+c*
- Identity element: It is zero, *a+0=a*
- Symmetric element: the symmetric of *a* is *-a,* since *a+(-a)=0.*
If a, b, and c are real numbers, multiplication has the following properties.
- Commutative property: *ab=ba*
- Associative property: *a(bc)=(ab)c*
- Identity element: It is one, *a\cdot 1=a*
- Symmetric element: for every *a≠0,* its symmetric is *1/a,* since *a\cdot \dfrac{1}{a}=0.*
- Distributive property: *a(b±c)=ab±ac*
- Multiplication by zero: if *ab=0,* then *a=0* or *b=0* (or both).
Limitations of real numbers
Integers were used to solve subtractions where the minuend is smaller than the subtrahend. With the introduction of rational numbers, we solved divisions that didn't result in integer outcomes. Now, with real numbers, which include both rational and irrational numbers, we solve a problem with nth roots, as it's no longer necessary to have nth power radicands for the result to belong to the same set.
However, there is still a limitation related to roots: roots with an even index of negative numbers cannot be extracted. For example, *\sqrt{-16}* has no solution in the set of real numbers, as there is no real number that, when squared, equals *-16.* To address this limitation, we move towards the final numeric set.
Subsets of real numbers
- Positive reals: *\mathbb{R}^+=\{x~\text{such that x is real and}~x>0\}*
- Negative reals: *\mathbb{R}^-=\{x~\text{such that x is real and}~x<0\}*
- Non-negative reals: *\mathbb{R}^+_0=\{x~\text{such that x is real and}~x≥0\}*
- Non-positive reals: *\mathbb{R}^-_0=\{x~\text{such that x is real and}~x≤0\}*
- Reals excluding zero: *\mathbb{R}^{*}=\{x~\text{such that x is real and}~x≠0\}*
Complex numbers
To overcome the aforementioned restrictions, we introduce a new set of numbers, which will include real numbers and must also allow finding roots of even index of negative numbers. We start by defining a new number, called the imaginary unit and represented by the letter *i*, which satisfies the following property:
*i^2=-1*
Note that *i* is not a real number, as no real number squared results in a negative number.
Numbers of the form *b\cdot i,* abbreviated as *bi,* where *b* is any real number, are called imaginary numbers, and binomials of the type *a+bi* where *a* and *b* are real, are called complex numbers. These complexes include as particular cases the real numbers (when b=0), and the imaginary numbers (when a=0). If a=b=0, then it is zero.
The set of all numbers corresponding to the form *a+bi,* where *a* and *b* are real numbers and *i^2=-1* is called the set of complex numbers and is symbolized by the letter C:
*\mathbb{C}=\{a+bi~~\text{such that a and b are real and}~~ i^2=-1\}*
In the complex number *a+bi,* the number *a* is called the real part, and the number *b* is called the imaginary part. Two complex numbers are equal if their corresponding real and imaginary parts coincide.
*a+bi=c+di* if and only if *a=c* and *b=d*
A root of an even index of a negative number can be rewritten and solved in this numeric set, considering that *i^2=-1.* For example:
*\sqrt{-4}=\sqrt{4\cdot (-1)}=\sqrt{4\cdot i^2}=\sqrt{4}\sqrt{i^2}=2i*
This result makes sense, as *(2i)^2=2^2\cdot i^2=4\cdot (-1)=-4*
Considering this, the limitation of real numbers regarding roots of even index of negative numbers is overcome.
Complex numbers have various utilities in mathematics and science; they serve, among other things:
- To represent voltages, currents, and components in electrical circuits and control systems.
- To describe wave phenomena, such as the behavior of electromagnetic waves and oscillations in mechanical systems.
Addition of complex numbers
The sum of two complex numbers is another complex number where the real part is the sum of the real parts, and the imaginary part is the sum of the imaginary parts.
*(a+bi)+(c+di)=(a+c)+(b+d)i*
Example:
*(2-4i) + (6+i)=*
*=(2+6) + (-4+1)i*
*=8-3i*
Multiplication of complex numbers
The multiplication of two complex numbers is carried out as follows:
*(a+bi)(c+di)=(ac-bd)+(ad+bc)i*
It is not necessary to memorize the definition; we can simply use the distributive property remembering that *i^2=-1*.
Example:
*(2+3i)(4-5i)=*
*=2.4+(2)(-5i)+(3i)(4)+(3i)(-5i)*
*= 8-10i+12i+(-3\cdot 5)i^2 *
*= 8+2i + (-15)(-1)*
*= 8+2i+15*
*= 23+2i*
According to these definitions, when adding or multiplying two complex numbers, the result will always be another complex number. It can also be shown that these operations are commutative and associative, and that multiplication is distributive with respect to addition; that is, if *u, v, w* are complex numbers, then:
*u+v=v+u*
*uv=vu*
*(u+v)+w=u+(v+w)*
*(uv)w=u(vw)*
*u(v+w)=uv+uw*
Also, the neutral element for addition is 0, which can be expressed as *0+0i.* The additive inverse of the complex number *a+bi* is the complex number *-a-bi,* because
*(a+bi)+(-a-bi)=[a+(-a)]+[b+(-b)]i=0+0i*
The multiplicative inverse (or reciprocal) of the complex number *a+bi* is defined as *\dfrac{1}{a+bi}.* Thus,
*(a+bi)\cdot \dfrac{1}{a+bi}=1*
Division of complex numbers
The division of complex numbers is carried out by multiplying the numerator and denominator by the complex conjugate of the denominator, which results from changing the sign of its imaginary part, and then developing the corresponding operations.
*\dfrac{a+bi}{c+di}=\dfrac{a+bi}{c+di}\cdot \dfrac{c-di}{c-di}*
For example:
*\dfrac{2+3i}{5-4i}=*
*=\dfrac{(2+3i)(5+4i)}{(5-4i)(5+4i)}*
*=\dfrac{10+8i+15i+12i^2}{5^2-(4i)^2} *
*=\dfrac{10+23i-12}{25-16i^2} *
*=\dfrac{-2+23i}{25+16} *
*=\dfrac{-2+23i}{41}*
In summary, by introducing complex numbers, we have overcome the limitation of real numbers and the "prohibited" operations are repealed, except for division by zero. One might then think of a further extension of the field of numbers that would lift this restriction; but there is a theorem, called the final theorem of arithmetic, which assures us that the largest set of numbers that exists is that of complex numbers.
FAQs
What was the first numeric set known to humanity?
The first numeric set known to humanity was the set of natural numbers. These are the numbers used to count elements in a set: 1, 2, 3, 4, 5, etc.
What set of numbers do roots belong to?
All square, cubic, and higher-order roots belong to the set of complex numbers.
What is the numeric set that includes all others?
The numeric set that includes all others is the set of complex numbers. This set includes real and imaginary numbers and is the widest set of all numbers.
What is the difference between natural numbers and integers?
The difference between natural numbers and integers lies in the inclusion of zero and negative numbers in the set of integers. Natural numbers are 1, 2, 3, 4, 5, …, while integers also include zero and negatives: …, -3, -2, -1, 0, 1, 2, 3, …
What is the difference between a real number and a complex number?
The main difference between a real number and a complex number is that a real number is any number that can be found on the real number line, including rational and irrational numbers, while a complex number is a combination of a real number and an imaginary number, represented in the form a+bi, where a and b are real and i is the imaginary unit.

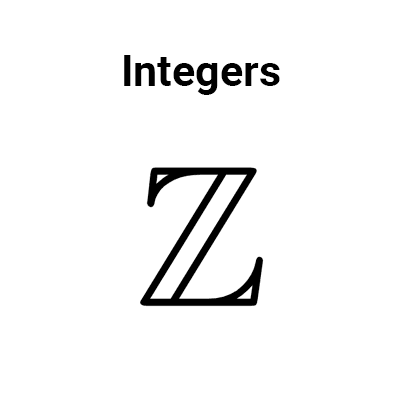

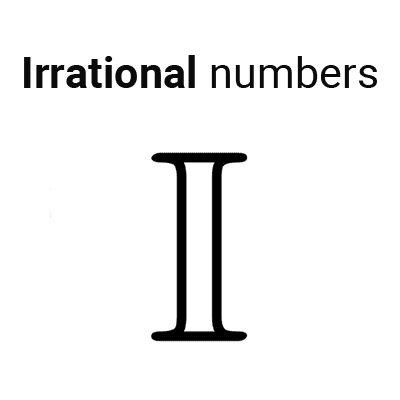




Other articles that may interest you