What is a function in Math?

In this article we explain what a function is in mathematics, how it is symbolized, ways of classification and examples of functions.

What is a function?

A function is a rule that assigns to each element of a set, called domain, a unique element of another set, called codomain.

We speak of a function or functional relationship when we encounter relationships between two sets of elements, in which each element of the first set is matched with only one element of the other set. For example, to each person corresponds an age, to each state corresponds a governor, to each word corresponds an initial letter, etc.

However, not all relationships between sets are functions. For example, the "is a parent of" relationship between people is not a function, as a person can have more than one child, and some people may have no children.

In mathematics, it is common to work with relationships of two variable quantities where one depends on the other. For example, the area A of a circle depends on its radius, and it is given by the expression A=πr². The relationship between these quantities is a function because to each value of the radius corresponds a unique value of the area. Mathematically, we can further clarify the concept of a function through the following definition.

Definition: a function f is a rule that assigns to each element x of a set A, a unique element y of a set B. The set A is called the domain of f. The set B is called the codomain, and the set of y in B is called the range of f.

Given a function f, the element y of the range corresponding to a chosen x in the domain is the value of the function at x, or the image of x, denoted by f(x). This symbol is read "f of x" or "f at x," and it is clear that y=f(x). The value of y depends on the choice of x, so it is called the dependent variable; x is called the independent variable.

It is useful to consider a function as a machine. If x is in the domain of the function f, then when x enters the machine, it is accepted as input, and the machine produces an output y=f(x) according to the function's rule. The input is the independent variable, and the output is the dependent variable.

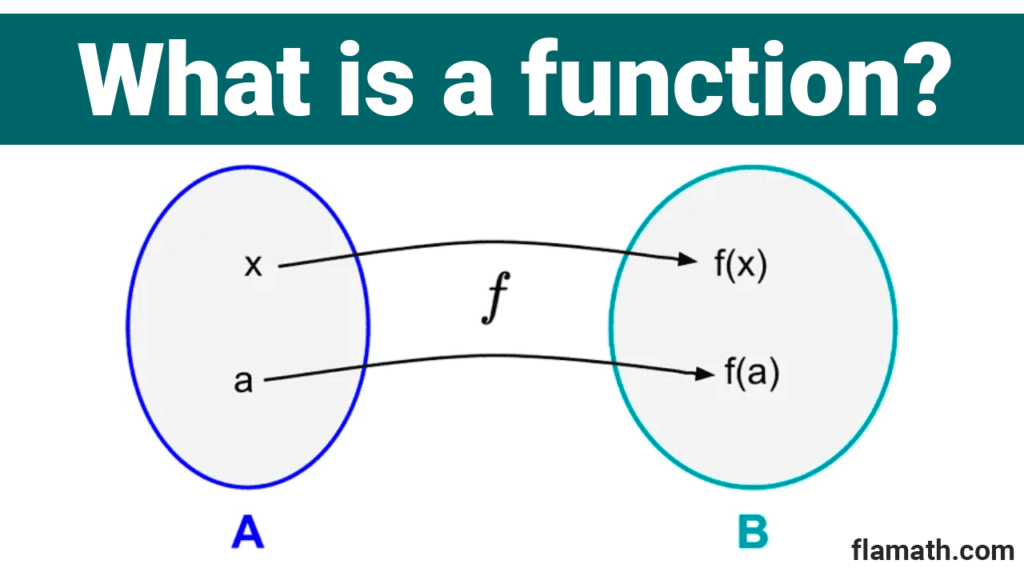
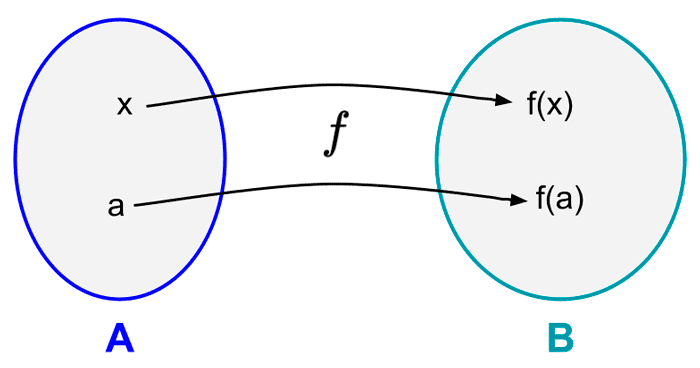
Another way to represent a function is through an arrow diagram. Each arrow connects an element of A with its corresponding element in B. In the following graph, it can be observed that x is related to f(x) and a is related to f(a). The set A is usually called the domain set and the set B codomain set.

For example, the rule for squaring a number is given by the equation *f(x)=x^2* or *y=x^2.* The value of f at *x=2* is obtained by substituting *x* into the formula:

*f(2)=(2)^2=4*

Thus, the element *x=2* corresponds to the element *y=4* according to the rule of the function f.

From the definition, we can say that characteristics of a function are:

• Existence: for each element of the domain, there must exist an image in the codomain. There cannot be elements in the domain without an associated image.
• Uniqueness: each element of the domain must have a unique image in the codomain. This means there cannot be two different images for the same element of the domain.

The elements of a function are:

• Domain: it is the set of all possible input values for which the function is defined.
• Codomain: it is the arrival set of the function, which contains all output values.
• Range: it is the set of all output values and is within the codomain. The range is not necessarily equal to the codomain.
• Rule of correspondence: it dictates how the elements of the domain are related to those of the codomain. It can be an algebraic expression, a table, a graph, or a verbal description. Visit ways to represent a function.

The domain and range of a function can be any sets of objects, but in mathematics, especially in calculus, they are often sets of real numbers. Functions of this type are called real functions of real variable.

Notation

Functions are usually denoted with the symbol f(x), where f is the name of the function and x is the input value. In contexts other than mathematics, symbols such as F, G, H, f, g, h, p, q, etc., are often used for functions. Lowercase letters r, s, t, u, v, w, x, y, z are used for dependent or independent variables.

Thus, a function could be written as w=G(z) or v=h(t). For example, in the function *A=π r^2*, we identify that the independent variable is r and the dependent variable is A.

The common symbolism used in mathematical analysis to specify the domain and codomain is:

*f: A → B \\ \hspace{9mm} x→f(x)*

which reads as "f is a function defined from A to B, to element x corresponds f(x)".

For example, the function *f(x)=x^2* is expressed as:

*f: \mathbb{R} → \mathbb{R} \\ \hspace{6mm} x→x^2*

Examples

Next, we will see some examples of mathematical functions:

1. Every non-negative real number can be square rooted. The function *f(x)=\sqrt{x}* takes a number x and returns its square root.
2. The function *y=x^2* relates each real number x to its square y.
3. The function *g(x)=|x|* assigns to each real number its absolute value.
4. The area of a circle depends on its radius. The formula *A=\pi r^2* gives us the area A of a circle with radius r.
5. The function *y=\frac{1}{x}* matches each non-zero real number to its multiplicative inverse, also called reciprocal.
6. The function *h(x)=\ln(x)* assigns to each positive real number x its natural logarithm.
7. Every real number has a cubic root, the function *y=\sqrt[3]{x}* relates each number x to its cubic root y.
8. The function described by the formula *v=\cos(u)* assigns to each real number u the value of its trigonometric cosine.
9. The area of a square depends on the length of its side, so if the side is *x*, the area of the square is given by the function *A(x)=x^2.*
10. Every real number has a double, which is obtained by multiplying it by 2. The function *f(x)=2x* takes a number x as input and outputs its double.

The following are examples of functions that may or may not be given by an equation:

1. The temperature at which water boils depends on the altitude above sea level.
2. The price of a house depends on its distance to the city center.
3. The level of air pollution depends on vehicular traffic in an urban area.
4. The time required to complete a task depends on the individual's level of experience.
5. The growth of a plant depends on the availability of nutrients in the soil.
6. The number of bird species in an area depends on the type of habitat available.
7. The distance traveled by an object from an initial point along a straight path depends on its velocity.
8. The interest rate paid for an investment depends on how long the money remains invested.

Here are some examples of relationships that are not functions:

• The relationship between the coordinates of points (x, y) on a circle of radius r is given by the equation *x^2+y^2=r^2.* This equation does not describe a function because it does not satisfy uniqueness. For example, the value *x=0* is related to *y=r* and *y=-r* at the same time.
• The equation *x=y^2,* if we consider x as the independent variable, does not correspond to a function for the same reasons as the previous example.
• The relation "less than" *x<y* is not a function, because one number x can be less than many numbers y. For example, *x=2* is related to *y=3; y=3.5; y=10,* etc.
• The relation "y is a multiple of x" is not a function because a number can have infinite multiples.

Types of functions

Functions can be classified according to different criteria, the most common being according to the relationship between their elements and according to the rule of definition.

According to the relationship between their elements

For this classification, we base ourselves on the relationship between the elements of the domain, codomain, and range.

• Injective functions: are those where no two distinct elements of the domain have the same image.
• Surjective functions: are those where the codomain is equal to the range.
• Bijective functions: are those that are both injective and surjective at the same time.

According to the rule of definition

For this classification, we base ourselves on the equation or formula that defines the function.

• Algebraic functions: are those that can be obtained from polynomial functions by addition, subtraction, multiplication, division, exponentiation, or radical. In this group, we have linear, constant, quadratic, cubic, rational, irrational functions, among others.
• Transcendental functions: are those that cannot be obtained through elementary operations of polynomial functions and transcend the field of algebra. In this group, we have exponential, logarithmic, trigonometric, and hyperbolic functions.

Other ways to classify functions include: according to their symmetry into even or odd, according to their periodicity into periodic or non-periodic, according to their continuity into continuous or non-continuous, according to their monotonicity into increasing or decreasing, etc.

Formal definition of function

From algebra, a function is defined as a particular case of a binary relation between sets, where there cannot be two ordered pairs with the same first component but different in the second. In other words, a function is a set of ordered pairs (x, y) where if (x, y) and (x, z) belong to the function, then y=z.

Definition: f is a function from A to B if and only if f is a relation from A to B that satisfies the following conditions:

1. Existence postulate: every element of the set A has a corresponding element in B. In symbols: *\forall x \in A \ \exists y \in B / (x, y) \in f*
2. Uniqueness postulate: the corresponding element of an element from set A is unique. In symbols: *(x, y) \in f \land (x,z) \in f → y=z*

Symbolically, uniqueness is established by stating that if an element of A has two corresponding elements, then those correspondents are equal.

FAQs

Infographics