
Even and odd functions
In this article we explain the concept and definition of even and odd functions along with examples, graphs, ways to determine parity and the mathematical properties of these functions.
Table of Contents
Definitions
A even function is one that satisfies that any value in its domain has the same image as the opposite value. In symbols:
*f(x)=f(-x)* for every x in the domain
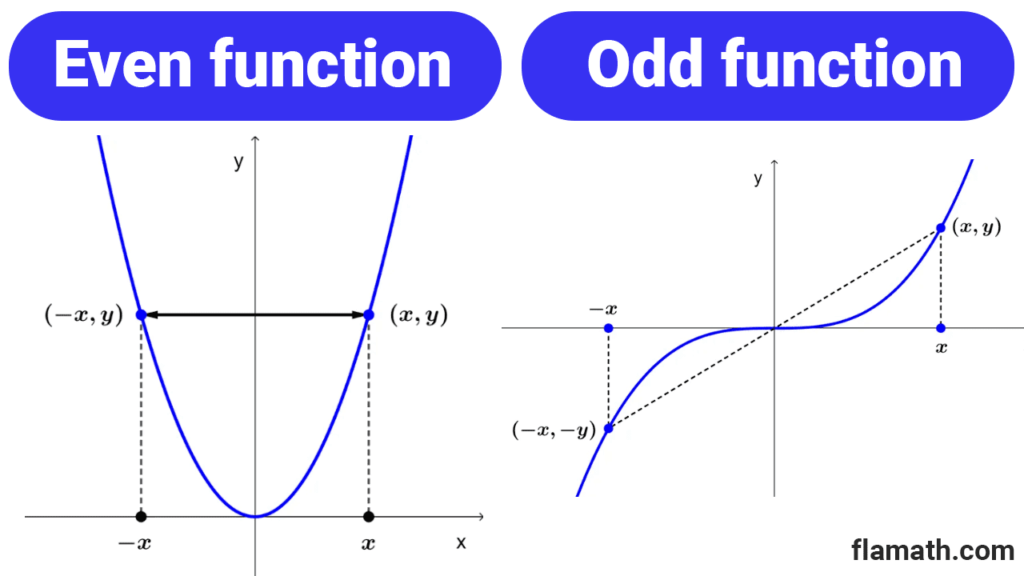
The graph of a even function is symmetric about the y-axis.
An odd function is one that satisfies that any value in its domain has as an image the opposite of the image of the opposite value. In symbols:
*f(x)=-f(-x)* or equivalently *f(-x)=-f(x)* for every x in the domain
The graph of an odd function is symmetric with respect to the origin of coordinates.
The names even and odd arise from the powers of x, as we can notice that functions with even exponent of x are even functions, and those with odd exponent are odd functions:
- Given *f(x)=x^2*, it can be seen that *f(-x)=(-x)^2=x^2=f(x)*, thus fulfilling the definition of an even function.
- Given *f(x)=x^3*, we see that *f(-x)=(-x)^3=-x^3=-f(x)*, therefore it is an odd function.
The same occurs with other powers of the same nature, for example:
- *f(x)=x^5* is an odd function because *f(-x)=(-x)^5=-x^5=-f(x)*
- *g(x)=x^8* is an even function since *g(-x)=(-x)^8=x^8=g(x)*
The geometric significance of an even function is that its graph is symmetric with respect to the y-axis. In other words, if we have the graph for *x≥0* (the right side of the plane), we can obtain the complete graph by reflecting that part with respect to the y-axis. In other words, a reflection with respect to the ordinate axis leaves the graph unchanged.
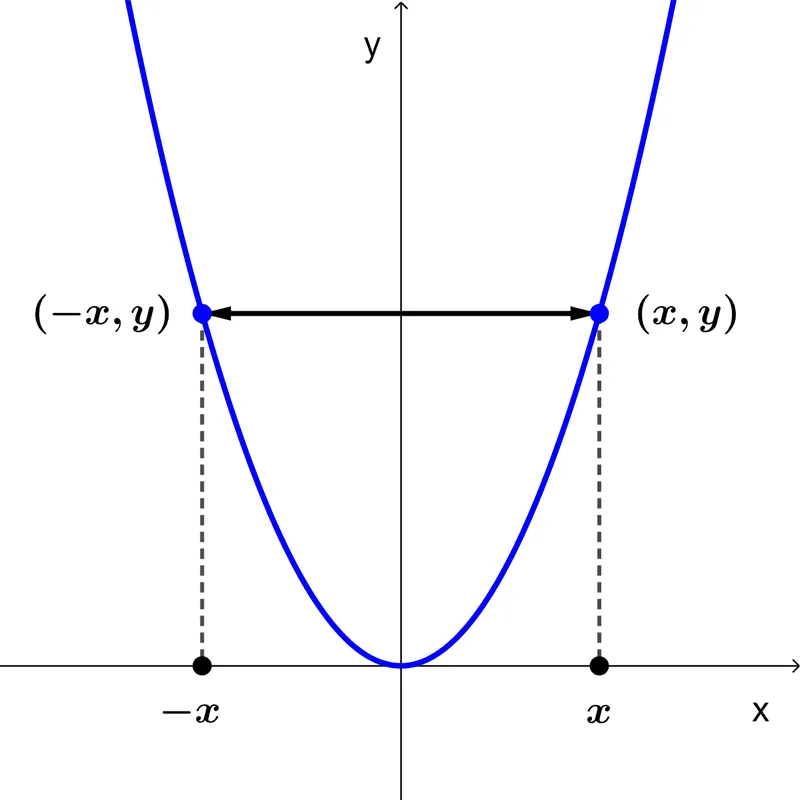
In the case of an odd function, its graph is symmetric with respect to the origin of coordinates. If we have the graph for *x≥0*, we can obtain the complete graph by rotating that segment 180° around the origin of coordinates.
How to know if a function is even or odd
Given a function, if we have the graph, we can check if it is symmetric with respect to the y-axis or with respect to the origin of coordinates to reach a conclusion about its parity.
We can also analyze it algebraically to determine if it is even or odd by finding the image of -x and verifying if any of the definitions are met. There are functions that are neither even nor odd; this occurs when none of the definitions are satisfied.
Steps to determine algebraically whether a function is even or odd
- Calculate the image of -x. This is achieved by replacing x with -x in the equation.
- Simplify the resulting expression. Perform all operations to obtain a simple form of the equation.
- Analyze the final equation. If the expression is equal to the original equation, then the function is even. If the expression is the opposite of the original equation, then the function is odd.
Example 1: *f(x)=x^2+1*
Previously, we saw that *y=x^2* is an even function; we will see what happens in this case.
We calculate *f(-x)*:
*f(-x)=(-x)^2+1=x^2+1=f(x)*
Since it satisfies the first definition, *f* is an even function.
Example 2: *f(x)=\dfrac{1}{x}*
We have a rational function; we calculate *f(-x)*:
*f(-x)=\dfrac{1}{-x}=-\dfrac{1}{x}=-f(x)*
Since it satisfies the second definition, the function is odd.
Example 3: *f(x)=3x^2+2x+1*
We calculate *f(-x)*:
*f(-x)=3(-x)^2+2(-x)+1=3x^2-2x+1*
Neither of the definitions is satisfied; therefore, the function is neither even nor odd.
Example 4:
*f(x)=\begin{cases} -1 \hspace{5mm} \text{if} \ x<0 \\1 \hspace{7.5mm} \text{if} \ x>0 \end{cases}*
In this case, we have a piecewise function, so we need to pay more attention when verifying the parity as we did before.
We calculate *f(-x)*:
When *x<0, f(x)=-1,* but *-x>0*, so *f(-x)=1=-f(x)* (in the first segment).
When *x>0, f(x)=1,* but *-x<0*, so *f(-x)=-1=-f(x)* (in the second segment).
Since the second definition is satisfied in both segments, the piecewise function is odd.
Parity of trigonometric functions
The trigonometric functions sine, cosine, and tangent are odd, even, and odd, respectively. This is due to the properties verified by the opposite of a number in their arguments.
*f(x)=\sin{x}→f(-x)=\sin(-x)=-\sin{x}=-f(x).* Therefore, sine is an odd function.
*f(x)=\cos x→f(-x)=\cos(-x)=\cos x=f(x).* Therefore, cosine is an even function.
*f(x)=\tan x→f(-x)=\tan(-x)=-\tan x=-f(x).* Therefore, tangent is an odd function.
The following properties can also be demonstrated:
- The cosecant function is odd.
- The secant function is even.
- The cotangent function is odd.
Properties of even and odd functions
Even and odd functions fulfill a series of properties, which are:
- Every real function is equal to the sum of an even function and an odd function.
- The constant function 0 is the only one that is both even and odd at the same time.
- The product of two even functions is an even function.
- The product of two odd functions is an even function.
- The product of an even function and an odd function is an odd function.
- The sum of two even functions is an even function.
- The sum of two odd functions is an odd function.
Demonstrations
Property 1:
We want to demonstrate that any function with domain *\mathbb{R}* can be written as the sum of an even function and an odd function. This can be achieved using the following identity:
*f(x)=\dfrac{1}{2}[f(x)+f(-x)]+\dfrac{1}{2}[f(x)-f(-x)]*
The first bracket encloses an even function, and the second one an odd function.
For example, with *f(x)=3x^2+2x+1* we can perform calculations to discover that it is the sum of the even function *3x^2+1* and the odd function *2x.*
Property 2:
We want to demonstrate that the function *f(x)=0* is the only one that is both even and odd at the same time.
Indeed, we seek a function that satisfies *f(x)=f(-x)=-f(-x)*
From the second and third equalities, we derive that a number must be equal to its opposite, which only happens when that number is zero, hence *f(x)=0*
Property 3:
We aim to demonstrate that the product of two even functions is an even function.
Indeed, suppose two functions f and g are even. Then it follows that *f(x)=f(-x)* and *g(x)=g(-x)*.
Let *h* be the product function: *h(x)=f(x)\cdot g(x).* It is verified that *h(-x)=f(-x) \ g(-x)=f(x) \ g(x)=h(x).* Thus, h is also an even function.
Property 4:
We aim to demonstrate that the product of two odd functions is an even function.
Suppose two functions f and g are odd. Then it follows that *f(-x)=-f(x)* and *g(-x)=-g(x)*
Let h be the product function: *h(x)=f(x) \cdot g(x).*
It holds that:
*h(-x)=f(-x) \cdot g(-x)*
*=[-f(x)] \cdot [-g(x)]*
*=(-1) f(x) \cdot (-1)g(x)*
*=(-1)(-1)f(x) \cdot g(x)*
*=f(x) \cdot g(x)*
*=h(x)*
Thus, the product function is even.
Property 5:
We aim to prove that the product of an even function and an odd function is an odd function.
Let *f* be an even function and *g* be an odd function. It holds that *f(-x)=f(x)* and *g(-x)=-g(x)*
Let *h* be the product function: *h(x)=f(x) \cdot g(x)*
It is verified that:
*h(-x)=f(-x) \cdot g(-x)*
*=f(x) \cdot [-g(x)]*
*=-[f(x) \cdot g(x)]*
*=-h(x)*
Therefore, it is demonstrated that h is an odd function.
Property 6:
We aim to demonstrate that the sum of two even functions is an even function.
Let *f* and *g* be two even functions. Then *f(-x)=f(x)* and *g(-x)=g(x)*
Let h be the sum function: *h(x)=f(x)+g(x)*
It holds that *h(-x)=f(-x)+g(-x)=f(x)+g(x)=h(x)*
Therefore, the sum function is even.
Property 7:
We aim to prove that the sum of two odd functions is an odd function.
Let *f* and *g* be two odd functions. Then *f(-x)=-f(x)* and *g(-x)=-g(x)*
Let *h* be the sum function: *h(x)=f(x)+g(x)*
It holds that *h(-x)=f(-x)+g(-x)=-f(x)-g(x)=-[f(x)+g(x)]=-h(x)*
Therefore, the sum function is odd.
FAQs
What is an even function?
An even function is one that satisfies that any value in its domain has the same image as the opposite value. That is, f(x)=f(-x). The graph of an even function is symmetric about the y-axis.
What is an odd function?
An odd function is one that satisfies that any value in its domain has as its image the opposite of the image of the opposite value. That is, f(x)=-f(-x). The graph of an odd function is symmetric with respect to the origin of coordinates.
How to determine algebraically even and odd functions?
To determine that a function is even, one must prove that f(-x)=f(x) for all x in the domain. To determine that a function is odd, one must prove that f(-x)=-f(x) for all x in the domain.
Can a function be both even and odd at the same time?
The only function that is both even and odd at the same time is the constant zero function, the others cannot be both simultaneously.
How do you know if the graph of a function is even or odd?
If the graph is symmetric about the y-axis, then the function is even. If the graph is symmetric about the point (0,0), then the function is odd. If neither occurs, then the function is neither even nor odd.
Are trigonometric functions even or odd?
The trigonometric functions sine and tangent are odd. The cosine function is even.
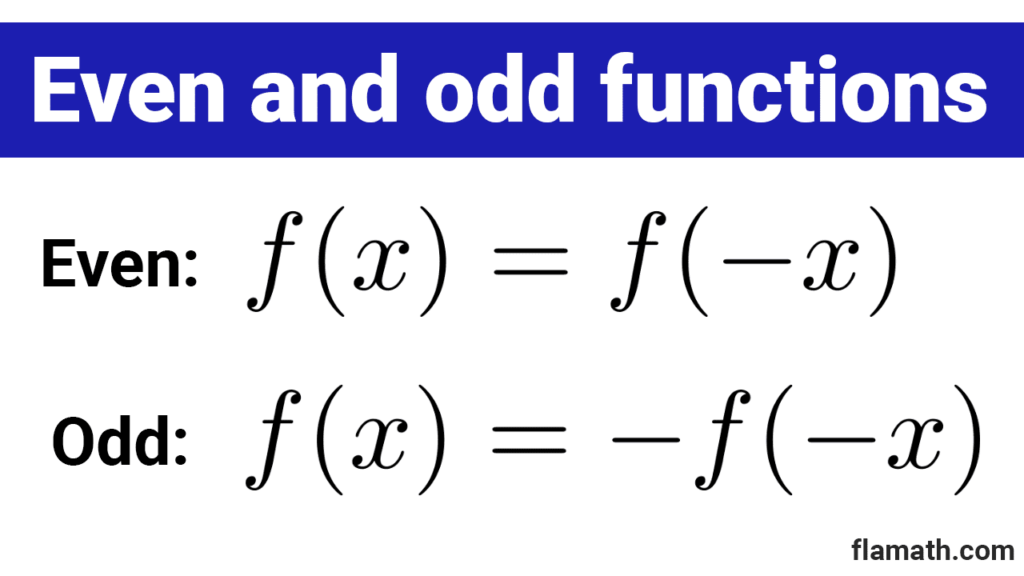




Other articles that may interest you