Cardinality of sets
In this article we explain what it is and how to calculate the cardinal of a set. We will see examples with finite and infinite sets and special properties.
Table of Contents
What is the cardinal of a set?
The cardinal of a set is the number of different elements it contains. The cardinal of a set A is represented by |A| or Card(A).
For example, the set A={a, b, c} has three elements, so its cardinality or size is that number: |A|=3. The set B={1, 2, 1} has two different elements, as "1" is written twice, therefore |B|=2.
If two sets have the same cardinality, then they are said to be equivalent. For example, the sets C={6, 9, 0} and D={p, q, r} both have three different elements, therefore, they are equivalent and we can write |C|=|D|.
The cardinality of a set can be finite or infinite. For finite sets, like the previous examples, the cardinality is a non-negative integer representing the number of different elements. For infinite sets, such as numeric sets, a special symbology is adopted.
Cardinal of a finite set
To calculate the cardinality of a finite set, simply count the number of unique elements it has.
Examples
- A = {1, 2, 3, 4, 4, 5} has five different elements, because the element "4" is repeated twice, so it is counted only once. Therefore, the cardinal number of A is 5: |A|=5
- B = {-1, 5, 3, 7} has four unique elements, therefore, its cardinality is that number: |B|=4
- C={green, blue, purple, blue} has three unique elements ("blue" is repeated twice and is counted only once), so |C|=3.
- D = {3, a, e, i, o, u, 3, o, 3} has six different elements, as "3" and "o" are repeated more than once and are counted only once. So, the cardinality is six: |D|=6
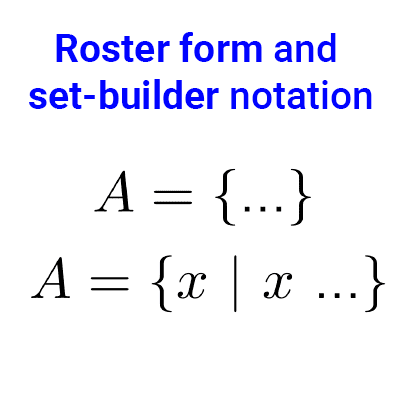
If the set is defined by set-builder notation, first it must be written by roster form (if possible) to count its elements and find its cardinality.
Examples
- J = {x | x is a letter of the word “Thursday”} is defined in set builder notation, written by listing it is J = {t, h, u, r, s, d, a, y}, which has five different elements, because one of the letters is repeated twice, so: |J|=5.
- The set E = {x | x+1=3} is written in set builder notation. Its roster form equivalent is E={2}, which has only one element, therefore, its cardinality is one: |E|=1. Sets whose cardinalities are equal to 1 are called singleton set, in this example, E is a singleton set.
Exercise: determine the cardinality of the following sets.
A = {x | x is a vowel}
B = {x | x is a natural number, even, and less than or equal to 12}
C = {x | x-1=0}
D= {x, y, z, w, y}
Solutions:
|A|=5
|B|=6
|C|=1
|D|=4
Properties
The cardinality of a finite set satisfies some properties that can be useful for its calculation.
1) Empty set cardinality
The cardinality of the empty set is zero, that is, |Ø|=0. This is evident because the empty set has no elements.
2) Subsets cardinality
If a set A is a subset of another set B, then the cardinality of A is less than or equal to the cardinality of B. Symbolically, if A ⊆ B, then |A| ≤ |B|.
If A is a proper subset of B, then the cardinality of A is strictly less than the cardinality of B. In symbols, if A ⊂ B, then |A| < |B|.
3) Union cardinality
The cardinality of a union of two sets is the sum of the individual cardinalities minus the cardinality of the intersection of the sets. In symbols:
|A ∪ B| = |A| + |B| - |A ∩ B|
If the sets A and B are disjoint (have no elements in common), then the cardinality of their union is simply the sum of their individual cardinalities, i.e.,
|A ∪ B| = |A| + |B|
4) Intersection cardinality
The cardinality of the intersection of two sets is the sum of the individual cardinalities minus the cardinality of the union of the sets. That is:
|A ∩ B| = |A| + |B| - |A ∪ B|
If A and B are disjoint sets, then the cardinality of their intersection is zero.
5) Difference cardinality
The cardinality of the difference between two sets A and B is equal to the cardinality of A minus the cardinality of the intersection of A and B, that is:
|A - B| = |A| - |A ∩ B|.
6) Complement cardinality
The cardinality of the complement of a set is equal to the cardinality of the universal set minus the cardinality of the set, i.e.,
|A’| = |U| - |A|
7) Cartesian product cardinality
The cardinality of the Cartesian product of two sets A and B is the product of their respective cardinalities, that is:
|A × B| = |A| ⋅ |B|
8) Power set cardinality
The cardinality of a power set is equal to 2 raised to the number of elements of the set. If a set has n elements, then the cardinality of its power set *2^n.*
Cardinal of an infinite set
The cardinal of an infinite set is expressed with special symbols since the number of elements cannot be counted. Mathematically, the cardinal of an infinite set is a transfinite number.
For example, the cardinal of the set of natural numbers is symbolized as ℵ₀ (aleph-zero). The cardinal of the set of real numbers is symbolized as c (continuum) or also ℵ₁ (aleph-one).
It is intuitive to think that infinite sets have the same number of elements because they are infinite. However, this is not the case, and it can be demonstrated that there are infinite sets that are "larger" than other infinite sets. In particular, the set of real numbers has more elements than the set of natural numbers: *c>ℵ₀*
It can also be demonstrated that infinite sets that seem to have more elements than others actually have the same number. Thus, the cardinals of the set of integers and the set of rational numbers are equal to the set of natural numbers: |Q| = |Z| = |N| = ℵ₀. Also, any two intervals of real numbers have the same number of elements: c.
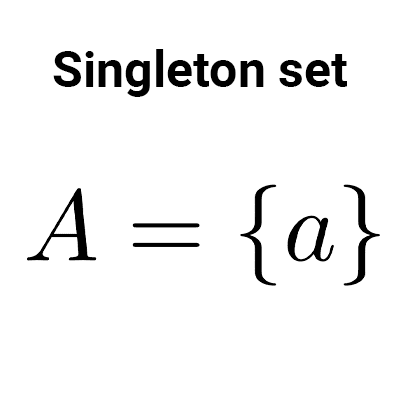
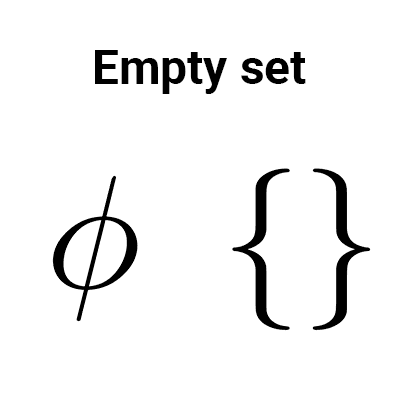
Other articles that may interest you