Subset
In this article we explain what is a subset of a set, the types that exist with examples and the properties they fulfill.
Table of Contents
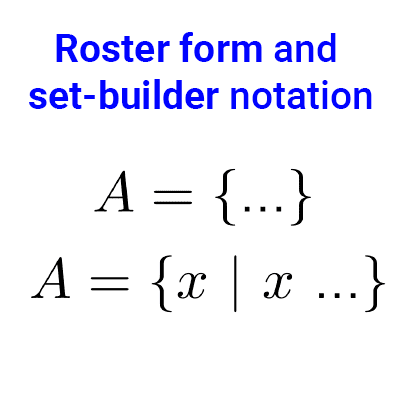
What is a subset?
A set is a subset of another if every element of the first set is also an element of the second, this relationship is symbolized by ⊆:
*A ⊆ B~* if and only if *~∀x: (x∈A → x∈B)*
If there is at least one element of A that is not in B, then A is said to not be a subset of B and is symbolized as A ⊈ B.
Examples
- The set A = {a, b} is a subset of B = {a, b, c, d} because the elements of A are also inside B, then A ⊆ B.
- The set C = {0, 1, 2, 3} is a subset of D = {-1, 0, 1, 2, 3, a, b}, because every element of C is also contained in D, then C ⊆ D.
- The set P = {p, q, r, s} is not a subset of Q = {p, r} because P has elements that are not in Q, then: P⊈Q. However, we can notice that Q is a subset of P, then Q⊆P.
- The set of all mammals has as a subset the set of all humans, because every human is a mammal.
- The set M = {-1, 1} is a subset of N = {1, -1}, and in turn N is a subset of M. This occurs because both sets are equal, then M ⊆ N, N ⊆ M and M=N.
- The set of natural numbers is a subset of the set of integers, because every natural number is also an integer, then N ⊆ Z. However, as there are integers that are not natural numbers (negatives and zero), the reciprocal relationship is not true, Z is not a subset of N: Z ⊈ N.
- The set of all positive real numbers *\mathbb{R}^+* is a subset of real numbers, because every positive real number is also a real number: *\mathbb{R}^+⊆\mathbb{R}.*
- If we call T the set of all triangles, then the set E of equilateral triangles is a subset of T: E ⊆ T.
To show that a set is a subset of another, it suffices to prove that every element of the first set is also an element of the second.
The set containing all subsets of A is called a power set of A, and is symbolized as P(A). If A has n elements, its power set has *2^n* elements. That is to say, the number of subsets of a set of n elements is *2^n.*
Proper subset
A set is a proper subset of another if all elements of the first set are also elements of the second, but there are elements of the second that are not in the first, meaning they cannot be equal sets. This relationship is symbolized by ⊂:
*A ⊂ B~* if and only if *~∀x: (x∈A → x∈B)* and also *A\neq B*
If there is at least one element of A that is not in B, or if A and B are equal, then it is said that A is not a proper subset of B and is symbolized as A ⊄ B.
Examples:
- The set A = {a, b} is a proper subset of B = {a, b, c, d} because the elements of A are also inside B and there are elements of B that are not in A ("c" and "d"). Then A ⊂ B. Note that it also happens that A ⊆ B.
- The set M = {-1, 1} is not a proper subset of N = {1, -1} because both sets are equal, then M ⊄ N. However, it happens that M ⊆ N, that is, M is a subset of M, but it is not a proper subset.
- The set of natural numbers, besides being a subset of integers, is also a proper subset of it: N ⊂ Z.
Every proper subset is also a subset, as in the first example, but not every subset is a proper subset, as in the second example.
Properties of subsets
Subsets adhere to the properties of set inclusion relation:
- Every set is a subset of itself, that is, A ⊆ A.
- If one set is a subset of another and the latter is also a subset of the former, then both sets are equal. That is, if A ⊆ B and B ⊆ A, then A=B.
- If one set is a subset of another, and the latter is a subset of a third set, then the first set is also a subset of the third. That is, if A ⊆ B and B ⊆ C, then A ⊆ C.
- The empty set is a subset of any set, even of itself. In other words, Ø ⊆ A and Ø ⊆ Ø.
- All sets are subsets of the universal set U: A ⊆ U.
Notation
Below is a summary of the symbolism used to refer to subsets.
| Symbol | Meaning |
|---|---|
| A ⊆ B | A is a subset of B |
| A ⊈ B | A is not a subset of B |
| A ⊂ B | A is a proper subset of B |
| A ⊄ B | A is not a proper subset of B |


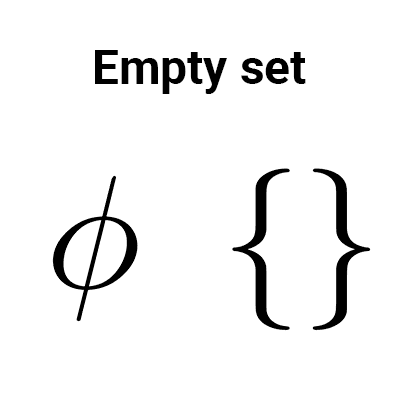
Other articles that may interest you