
Set inclusion
In this article we explain what is the inclusion of sets in discrete mathematics set theory, the types that exist, the properties they fulfill and examples of each one.
Table of Contents
What is set inclusion?
Inclusion is a relationship between two sets where all elements of the first set are also elements of the second. In other words, the first set is contained within the second. There are two types of inclusion: wide and strict.
Inclusion
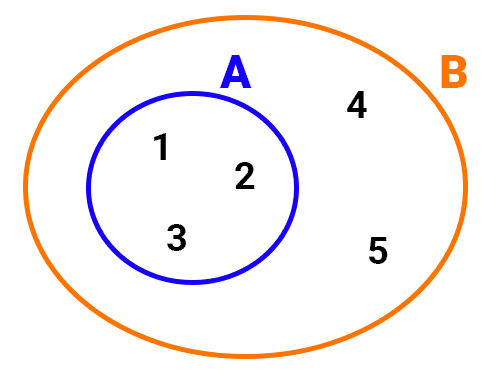
A set is included in another if the elements of the first set are also elements of the second, and the two sets can be equal. This relationship is symbolized by ⊆:
*A ⊆ B~* if and only if *~∀x: (x∈A → x∈B)*
If a set A is included in a set B, then A is called a subset of B. To indicate that a set is not included in another, the crossed-out symbol ⊈ is used. Thus, A ⊈ B means that A is not included in B.
Examples
- The set A = {1, 2, 3} is included in the set B= {1, 2, 3, 4, 5}, because the elements of A are also elements of B, so A ⊆ B.
- The set C = {a, b, c, d} is included in the set D = {1, 2, 3, a, b, c, d, e}, because every element of C is also contained in D, so C ⊆ D.
- The set M = {-1, 0, 1} is not contained in N = {1, 0} because M has elements that are not in N, so: M⊈N. However, we can notice that N is included in M, so N⊆M.
- The set E = {1, 2} is included in F = {2, 1}, because every element of E is also an element of F, so E ⊆ F. The reciprocal relationship is also true: F ⊆ E. This occurs because the sets E and F are equal.
- The set of natural numbers N is included in the set of integers Z, because every natural number is also an integer, so: N ⊆ Z. The reciprocal relationship is not true because there are integers that are not natural numbers (zero and negatives), so Z ⊈ N.
Based on the examples, we can say that to demonstrate that one set is included in another, it suffices to prove that every element of the first set is also an element of the second.
Properties of inclusion
Wide inclusion satisfies the following properties:
1) Reflexivity: every set is included in itself, that is, A ⊆ A.
2) Antisymmetry: if one set is included in another and vice versa, then both sets are equal. That is, if A ⊆ B and B ⊆ A, then A=B.
3) Transitivity: if one set is included in another, and the latter is included in a third, then the first set is also included in the third. That is, if A ⊆ B and B ⊆ C, then A ⊆ C.
4) The empty set is included in all sets, even in itself. That is, *Ø⊆A,* also *Ø⊆Ø.* The proof of this property is done from the definition:
*Ø ⊆ A~* if and only if *~∀x: (x∈Ø → x∈A)*
Since the proposition x ∈ Ø is false because the empty set has no elements, the implication x ∈ Ø → x ∈ A is true due to having a false antecedent. Therefore, Ø ⊆ A holds.
Strict inclusion
A set is strictly included in another if the elements of the first set are also elements of the second, but there are elements of the second set that are not in the first, meaning they cannot be equal sets. This relationship is symbolized by ⊂:
*A ⊂ B~* if and only if *~∀x: (x∈A → x∈B)* and also *A\neq B*
If a set A is strictly included in a set B, then A is called a proper subset of B. To indicate that a set is not strictly included in another, the crossed-out symbol is used ⊄. Thus, A ⊄ B means that A is not strictly included in B.
Examples
- The set A = {1, 2, 3} is strictly included in the set B = {1, 2, 3, 4, 5}, because the elements of A are also elements of B, and there are also elements in B that are not in A (the "4" and the "5"). So A ⊂ B.
- The set E = {1, 2} is not strictly included in F = {2, 1}, because although every element of E is also an element of F, there are no elements in F that are not in E. In other words, set F is not larger than E, therefore, strict inclusion does not hold: E ⊄ F.
Every strict inclusion is also a inclusion, but not every inclusion is strict. A set may not be strictly included in another, but it may still be included, as in the second example.
Notation
The following table summarizes the symbolism used for set inclusion.
| Symbol | Meaning |
|---|---|
| A ⊆ B | A is included in B |
| A ⊈ B | A is not included in B |
| A ⊂ B | A is strictly included in B |
| A ⊄ B | A is not strictly included in B |

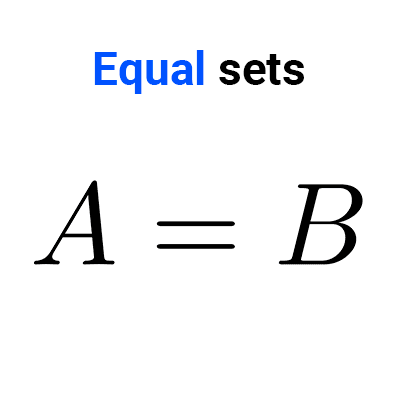
Other articles that may interest you