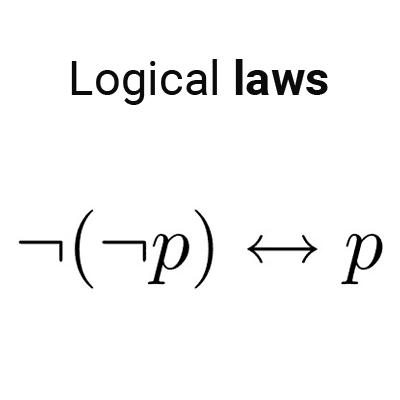
Discrete Mathematics Quantifiers
One part of mathematical logic is called predicate logic, where we work with expressions that can be converted into propositions. In this article we will see in detail what these expressions are and which are the ways to convert them into propositions.
Table of Contents
Propositional function
Definition: A propositional function (also called a propositional schema) is any expression capable of being a proposition.
For example, "x has black hair" is a propositional function, not a proposition because we don't know who x is.
We use a notation with uppercase letters and the variable in parentheses: *P(x), Q(x), R(x), etc.* We could also have more than one variable, for example *P(x,y), Q(x,y,z), etc.* In this article, we will work more with propositional functions of one variable. Let's see some examples of propositional functions with their corresponding notation:
- P(x): x has black hair.
- Q(x): x is a cat.
- R(x, y): x is the brother of y.
There are two ways to turn a propositional function into a proposition: by substitution or by quantification.
Substitution involves replacing the variable with a word. For example, in P(x): x has black hair, we could replace x with "John" thus arriving at the proposition P: "John has black hair." All the words by which the variable can be replaced belong to what is called a universe of discourse, where all the people, ideas, symbols, and other things that affect the variable are included. The elements of the universe of discourse are called individuals.
Quantification
Quantification involves preceding a propositional function with an element called a quantifier, transforming it into a proposition. There are two main types of logical quantifiers: the universal quantifier (∀) and the existential quantifier (∃).
For a P(x) propositional function, we express it as follows:
- *∀x: P(x)* is read as "for all x, P(x) is true" or "for any x, P(x) is true."
- *∃x/ P(x)* is read as "there exists an x such that P(x) is true" or "there exists at least one x such that P(x) is true."
The first proposition is true when all individuals in the universe of discourse satisfy the assertion. The second proposition is true when at least one individual satisfies the assertion.
By convention, a colon is used for the universal quantifier, and a slash is used for the existential quantifier. We can also quantify a propositional function in a way that specifies only one individual satisfies the assertion; in that case, we write *∃!x/P(x)* and read it as "there exists a unique x such that P(x) is true." This quantifier is known as the unique existence quantifier.
For example, with the propositional function P(x): x is a cat, if we want to say that all individuals in the universe of discourse are cats, we use the universal quantifier: ∀x: x is a cat. This is read as "for all x, it is true that x is a cat" or in everyday language, "all x are cats."
If we want to say that some individuals in the universe of discourse are cats, we use the existential quantifier: ∃x/ x is a cat. This is read as "there exists an x such that x is a cat" or in more natural language, "there exist x that are cats."
Quantifier scope
Both the universal and existential quantifiers apply to the propositional function closest to them, unless modified by parentheses. For example: ∀x: P(x) ∨ Q(x) is interpreted as [∀x: P(x)] ∨ Q(x). If we want the quantifier to apply to both functions, we should write ∀x: [P(x) ∨ Q(x)].
Negation of a quantifier
From natural language, we can deduce that to negate a universal property, for example, "all people are blond," it would be enough to show that there exist people who are not blond. Taking a general case P(x), in quantifier symbolism, we are stating the following:
¬∀x: P(x) ↔ ∃x/ ¬P(x) (the biconditional is interpreted as equivalence). In other words, it is not true that every x satisfies P(x) is equivalent to saying that there exist x for which ¬P(x) is true.
Similarly, with the existential quantifier: ¬∃x: P(x) ↔ ∀x/ ¬P(x). In other words, it is not true that there exist x satisfying P(x) is equivalent to saying that no x satisfies P(x), or for every x, it is not true that P(x) is satisfied.
Basically, negating a quantified proposition consists of changing the quantifier and negating the propositional function.
- To negate the universal quantifier, it is replaced by the existential quantifier, and the propositional function is negated.
- To negate the existential quantifier, it is replaced by the universal quantifier, and the propositional function is negated.
FAQs
What are logical quantifiers in discrete mathematics?
Logical quantifiers are symbols used in discrete mathematics to concisely express propositions involving variables and sets of elements. Quantifiers allow us to specify the number of elements that satisfy a certain property.
What are the 2 types of quantification?
The two main types of quantization are universal quantization and existential quantization. These are represented by the mathematical symbols ∀ (for universal quantifier) and ∃ (for existential quantifier).
What is the difference between the universal quantifier (∀) and the existential quantifier (∃)?
The universal quantifier (∀) is read as "for all" or "for every" and is used to express that a property is true for all elements of a set.
The existential quantifier (∃) is read as "exists" and is used to express that at least one element in a set has a certain property.
How do you negate statements containing quantifiers?
To negate a statement with universal quantifier (∀), logical negation is used and universal quantification is changed to existential. The negation of "for all x, P(x)" is "there exists some x for which P(x) is not satisfied".
To negate a statement with existential quantifier (∃), logical negation is used and existential quantification is changed to universal. The negation of "there exists some x such that P(x)" is "for all x, P(x) is not satisfied".
Can two quantifiers be used in the same logical proposition?
Yes, it is possible to use two or more quantifiers in the same logical proposition. For example, you can have a statement like "for all x, there exists y such that P(x, y)," which means that for every element x there is at least one element y that satisfies property P. The combination of quantifiers can express more complex and detailed relationships over sets and variables.
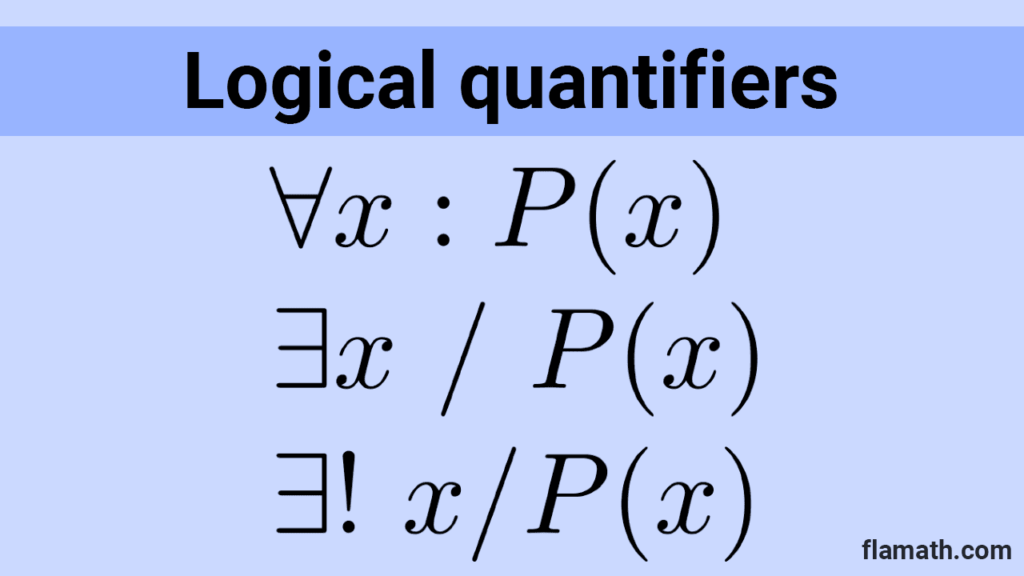

Other articles that may interest you