Rational function

In this article we explain the fractional rational functions going through their definition, examples, properties and elements such as domain, graph and asymptotes, among other things.

Definition and examples

A rational function is an algebraic function of the form *f(x)=\dfrac{p(x)}{q(x)}* where *p* and *q* are polynomial functions and *q(x)≠0.* In other words, a rational function is a ratio (quotient) of polynomial functions, hence its name.

Some examples of rational functions are:

*f(x)=\dfrac{x-1}{2x^3+x^2+27}*

*g(x)=\dfrac{-7x^2+2x+1}{x^5-3}*

*y=\dfrac{3}{x^2}*

*h(x)=\dfrac{x^3+2x^2-x}{x+1}*

*y=\dfrac{1+x}{1-x}*

The general equation for a rational function is:

*f(x)=\dfrac{a_nx^n+a_{n-1}x^{n-1}+...+a_1x+a_0}{b_mx^m+b_{m-1}x^{m-1}+...+b_1x+b_0}*

Note that every polynomial function is a rational function with a denominator of 1.

The highest power of the variable *x* in the numerator is the degree of the numerator, similarly occurs with the degree of the denominator. For example, *f(x)=\dfrac{x-1}{2x^3+x^2+27}* has a numerator of degree 1 and a denominator of degree 3. In *y=\dfrac{3}{x^2},* the degree of the numerator is zero (because it can be understood as *3x^0*), and the degree of the denominator is 2. The numbers multiplying the highest power of *x* are called leading coefficients.

Examples:

• *y=\dfrac{2x+1}{x^2+3x+3}* is a proper function, as the degree of the numerator is 1 and that of the denominator is 2, and *1<2.*
• *\dfrac{5x^4-x^2+3}{x^2+4}* is an improper function, as the degree of the numerator is 4 and that of the denominator is 2, and *4>2.*

Every improper rational function can be written as a sum of a polynomial function and a proper rational function. This is achieved by calculating the quotient between the numerator polynomial and the denominator.

If the numerator and denominator have no common factors, the function is said to be in minimal terms, simplified, or is irreducible. Otherwise, it is said to be reducible, such that repeated factors can be eliminated to obtain a simplified form.

For example, the function *f(x)=\dfrac{x^2-4}{x-2}* is reducible, as the numerator can be factored:

*f(x)=\dfrac{(x-2)(x+2)}{x-2}*

If *x≠2,* we can simplify as follows:

*f(x)=\dfrac{{\cancel{(x-2)}}(x+2)}{\cancel{x-2}}=x+2*

The new function coincides with the original at all points except *x=2,* where it is undefined. The importance of knowing whether a rational function is reducible or not will be seen later when calculating asymptotes.

Characteristics and properties

There are certain properties that characterize rational functions, the most important ones are:

• The domain of every rational function consists of all real numbers that do not make the denominator zero.
• Any rational function where the degree of the denominator is greater than or equal to the numerator has asymptotes, whether they are vertical, horizontal, or slant.
• Every rational function is continuous in its domain. The "jumps," "holes," or "breaks" that may occur in the graph happen at points that do not belong to the domain.

Elements of a rational function

We will describe below the main elements that allow us to perform the analysis of rational functions.

Domain

Example: *f(x)=\dfrac{x^3+15}{x^2-1}*

We find those values that make the denominator zero, in other words, we solve the equation:

*x^2-1=0*

The solutions are *x=-1* and *x=1,* therefore, these values are excluded from the domain:

*D_f=\mathbb{R}-\{-1,1\}*

Important: the domain is always determined from the original expression, no matter if this is the irreducible form or not.

Graph

The graph of a rational function can be very varied, to make it you have to pay attention to:

• The domain.
• Intersections with the axes.
• The degrees of the numerator and denominator.
• The asymptotes.

It is important to address the following questions:

• What happens to the values *f(x)* when *x* is close (but not equal) to a zero of the denominator?
• What can be said about the values of the function *f(x)* when the values of *x* grow or decrease without limits?

We will begin with the study of the asymptotes and see how they relate to the degrees of the numerator and denominator.

Asymptotes

An asymptote is a line toward which the graph of a function approaches as the independent variable tends to a certain value or grows or decreases without limits.

Rational functions can have vertical, horizontal, or slant asymptotes. If a function has a vertical asymptote, it may also have a horizontal one, but not a slant one (and vice versa).

It is often said that the graph of a function never touches an asymptote, but only approaches it; however, a rational function can intersect both a slant and a horizontal asymptote, but not a vertical one.

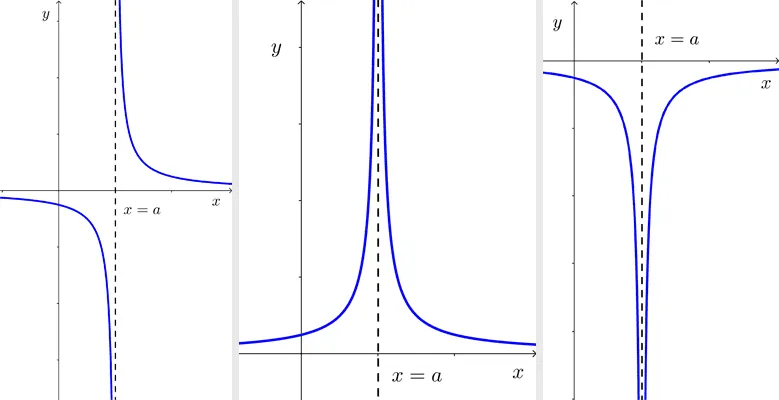
Vertical asymptote

The behavior of a rational function as it approaches a vertical asymptote is known as an infinite jump (because values tend to infinity). This causes a discontinuity in the graph.

Rational functions can have infinite vertical asymptotes. These occur at each root of the denominator that is not a root of the numerator. That is, if the denominator has a root at *x=a,* but this value is not a root of the numerator, then the function has a vertical asymptote with equation *x=a.*

Theorem: The graph of a rational function of the form *\dfrac{p(x)}{q(x)},* where *p(x)* and *q(x)* have no common factors, has the line *x=a* as a vertical asymptote when *q(a)=0*

In other words, the theorem states that an irreducible rational function has vertical asymptotes at all values that make its denominator zero. Knowing this, we have a way to find them.

Example: *f(x)=\dfrac{1}{x-1}*

The function is in irreducible form, and the value *x=1* makes the denominator zero; therefore, there is a vertical asymptote at this value. We will analyze what happens to the function as *x* approaches the number *1.*

*x*	*f(x)*
*0.9*	*-10*
*0.99*	*-100*
*0.999*	*-1000*
*1*	Does not exist
*1.001*	*1000*
*1.01*	*100*
*1.1*	*10*

As we get closer to *1,* the absolute values of *f(x)* become larger. Therefore, we confirm that there exists a vertical asymptote at *x=1.*

Important: If a rational function is not simplified, applying the theorem will result in an incorrect list of vertical asymptotes. If a value *x=a* nullifies both the numerator and the denominator, it means that *(x-a)* is a factor of both, which can be canceled out. This causes no infinite jump (no asymptote) at *x=a,* but rather a hole in the graph.

Horizontal asymptote

Definition: The line *y=c* is a horizontal asymptote of the graph of a rational function if the y-values approach *c* as *x* becomes extremely large in absolute value, that is, when it becomes increasingly positive or increasingly negative (tends to infinity or negative infinity).

The graph of a rational function can have at most one horizontal asymptote.

Example 1: *f(x)=\dfrac{x^2-5}{x^3+1}*

We are in the first case, as the degree of the numerator is less than the denominator. Therefore, the line *y=0* is the horizontal asymptote of the graph.

In a table, we can see that for larger or smaller values of *x,* the value of *f(x)* approaches zero.

*x*	*f(x)*
*-1000*	*-0.00099*
*-100*	*-0.0099*
*-10*	*-0.095*
*10*	*0.095*
*100*	*0.0099*
*1000*	*0.00099*

Example 2: *f(x)=\dfrac{3x^2}{5x^2-1}*

We are facing case 2, as both the numerator and denominator have the same degree. In this scenario, the line obtained from the ratio of the leading coefficients will be the horizontal asymptote. The leading coefficients of the numerator and denominator are 3 and 5, respectively, hence *y=3/5* is the horizontal asymptote of the graph.

Example 3: *f(x)=\dfrac{x^6}{x-1}*

We are in the third case: the degree of the numerator exceeds that of the denominator. Therefore, there is no horizontal asymptote. In these cases, under certain conditions, another type of asymptote may exist, which we will see next.

Oblique asymptote

Definition: A line *y=mx+b,* where *m≠0,* is called a slant asymptote, or oblique asymptote, of the graph of a rational function if the images approach the line when *x* becomes very large in absolute value, that is, when it becomes increasingly positive or negative (tends to infinity or negative infinity).

Example: *f(x)=\dfrac{x^2+1}{x-3}*

Since the degree of the numerator is one unit higher than the denominator, there exists an oblique asymptote. We extract it from the quotient of the polynomial division:

The line *y=x+3* is the oblique asymptote of the graph.

If a rational function has an oblique asymptote, it can have vertical asymptotes, but it cannot have a horizontal asymptote. The graph of a function can cut an oblique asymptote.

Roots

Let's remember that the roots or zeros of a function are the values where the function equals zero; geometrically, it's where the graph intersects the *x*-axis.

If a rational function *f(x)=\dfrac{p(x)}{q(x)}* is in irreducible form, the roots of the numerator polynomial *p(x)* are also the roots of the function *f.*

Example: *f(x)=\dfrac{x-3}{x^2+1}*

By analyzing the function, we conclude it's in irreducible form. Therefore, the function's roots are the roots of the numerator, i.e., we need to find the numbers that satisfy:

*x-3=0→x=3*

Thus, *x=3* is the zero of *f.*

It's crucial that the function is in irreducible form, as otherwise, we'll get an incorrect list of roots.

Intersection with y-axis

If zero is part of the domain of a rational function, the y intercept is guaranteed, and it will occur at *f(0).*

Example: *f(x)=\dfrac{1}{x-1}*

The number zero is part of the domain, as it does not make the denominator zero. Therefore, there is an intersection with the y-axis, which occurs at:

*f(0)=\dfrac{1}{0-1}=-1*

Special cases

We will see two particular cases of rational functions that are frequently studied.

Homographic function

The domain consists of all real numbers except those that make the denominator zero, meaning the excluded value is the one that satisfies:

*cx+d=0*

*x=-\dfrac{d}{c}*

*D_f=\mathbb{R}-\left\{-\dfrac{d}{c}\right\}*

The graph of the function has a vertical asymptote at this point, meaning *x=-\dfrac{d}{c}* is a vertical asymptote of the graph. Due to the absence of more roots of the denominator, this asymptote is unique.

The function may have a root at the value of *x* that satisfies *ax+b=0*, meaning at *x=-\dfrac{b}{a}.* If *a=0*, the function has no root.

If zero is within the domain, there is an intersection with the y-axis, which occurs at the image of this number:

*f(0)=\dfrac{a(0)+b}{c(0)+d}=\dfrac{b}{d}*

Homographic functions have a horizontal asymptote with an equation *y=\dfrac{a}{c}.* They never intersect this asymptote, thus only excluding a single number from their range; therefore:

*R_f=\mathbb{R}-\left\{\dfrac{a}{c}\right\}*

Function of inverse proportionality

Notice that this is a homographic rational function where *p(x)=k* and *q(x)=x.* For this reason, it inherits some of its elements.

Domain: *\mathbb{R}-\{0\}*

Range: *\mathbb{R}-\{0\}*

Horizontal asymptote: line *y=0* (the x-axis)

Vertical asymptote: line *x=0* (the y-axis)

Root: None

Intersection with the y-axis: None

FAQs

Infographics