
Real valued functions
In this section we will study a group of important functions in mathematical analysis: real functions of real variable (also called real-valued functions), that is, those where the variables are real numbers. We will analyze their definition, domain and range, graphs and we will see some examples of them.






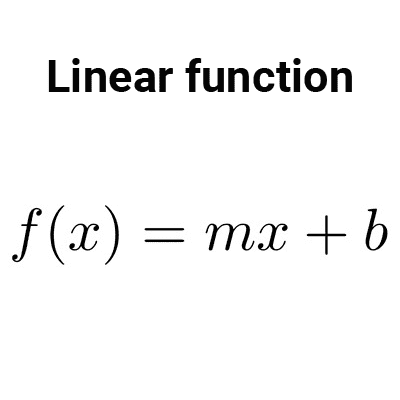


Articles
Table of Contents
What is a function
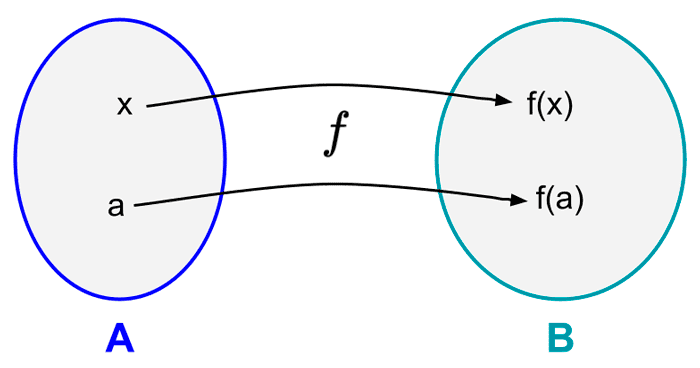
Recall that a function or application is a rule that assigns to each element of a set, called domain, a single element of another set, called codomain. Then, in real functions what will happen is that the domain and the range will be subsets of real numbers.
Definition
Let A and B be two subsets of real numbers. A real function of one real variable f is a rule that assigns to each real number from the set A, a unique real number from the set B.
The set A is called the domain of the function, the set B is called the codomain. The range is defined as the subset of B formed by all the images of the elements of A. It is possible that there are elements in the codomain that are not in the range of the function.
The typical symbology used in mathematical analysis is $$f: A\subseteq \mathbb{R} \rightarrow \mathbb{R}$$ which is read as "f is a function defined from real numbers to real numbers." Alternatively, we could write $$f: A\rightarrow B, A\subseteq \mathbb{R}, B\subseteq \mathbb{R}$$ which is interpreted as "f is a function defined from A to B, where both A and B are subsets of real numbers."
For the function f, to each element x in the domain A, there corresponds an element y in the range. This element y is called the value of the function f at x, or the image of x through f, and is denoted as f(x), read as "f of x." So, we can say that *y=f(x).* Since the value of y depends on the choice of x, it is called the dependent variable; x is called the independent variable. In this sense, the domain is the set of all possible values of x, and the range is the set of values of y that correspond to each x.
Note: In some literature, the element x in the domain of the function is often referred to as the "argument" or "pre-image" of the function.
The notation for functions can be confusing at first. Remember that f is the name of the function, and f(x) is the image of the element x in the domain of f. Therefore, it turns out that f(x) is an element of the range of the function, which is why we can write *y=f(x).*
Functions are often defined by a formula or equation that describes the relationship between the elements of the domain and the range. It may happen that a single rule is used to calculate the image of each element in the domain, or depending on the value of the independent variable, a different rule is used to calculate its image (step function).
For example: *y=6x^2+x+1 *
Using function notation, we can write this equation as
*f(x)=6x^2+x+1*
This notation is useful because it tells us several things:
- The independent variable is x.
- The dependent variable is f(x), which can be written as y.
- The name of the function is f.
- An element x in the domain is mapped to *f(x)=6x^2+x+1.*
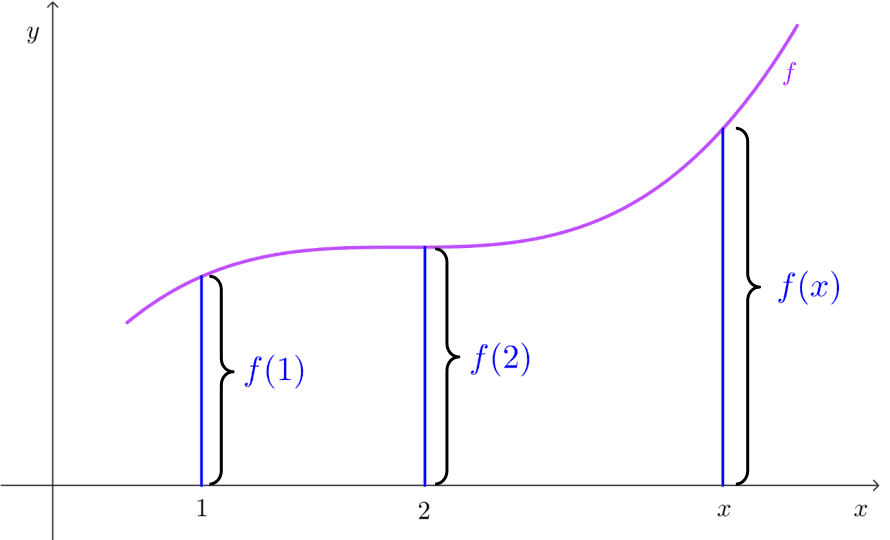
If we want to know, for example, what the value of the function is when x=3, we can simply ask, "What is *f(3)*?" The process of finding the value of y corresponding to a given x is called evaluating the function.
The role of the variable x in the equation can be understood as a placeholder to fill. For example, the function *f(x)=6x^2+x+1* can be described as *f(~~~)=6(~~~)^2+(~~~)+1,* where we use parentheses instead of x, and it could be read as "f of something is equal to six times that something squared, plus the something, plus one." To evaluate *f(-2),* we simply substitute *-2* for each pair of parentheses:
*f(-2)=6(-2)^2+(-2)+1*
*=6\cdot 4-2+1*
*=23*
Note: Although it is common to use f as a symbol to denote a function and x for the independent variable, other symbols can be used. As long as a function is well-defined, the symbols used to write it are not very important. As an example, the following equations all define the same function:
*f(x)=x^2-4x+5*
*f(t)=t^2-4t+5*
*g(s)=s^2-4s+5*
The letters commonly used to name functions are F, G, H, f, g, h, p, q, etc.; for variables, r, s, t, u, v, w, x, y, z are usually used.
Domain and range
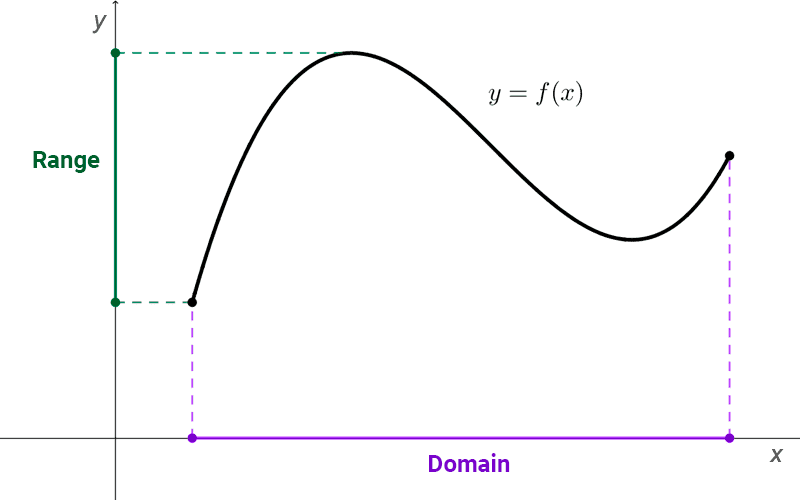
The domain or existence field of a function is the set of all possible values that the independent variable can take. The image set, range, or codomain is the set of all values that the dependent variable can take. In real functions, as expected, the domain and the range are subsets of real numbers.
Domain: it is the set of real numbers for which the function is defined, meaning that they have a real image through the function. It is denoted as *D_f* or *Dom(f)*
*D_f=\{x\in \mathbb{R}~|~\exist~ f(x)\}*
The domain of a function can be explicitly provided with it; otherwise, the domain will be taken as the largest set of real numbers that result in a real number as an image. In this latter case, it may be necessary to do some calculations using the equation.
Examples:
- The function *f(x)=\dfrac{1}{x^2-4},* *4≤x≤5* has an explicitly defined domain as *D_f=\{x~|~4≤x≤5\}=[4,5]*
- The function *g(x)=\dfrac{1}{x-1}* has an implicit domain which is *D_g=\{x~|~x≠1\}=\mathbb{R}-\{1\},* because the denominator cannot be zero.
It is convenient to review the notation of real intervals and sets to express the domains of functions.
Range: is the set of all real numbers that are images of the elements in the domain of the function. It is denoted as *R_f.*
*R_f=\{y\in \mathbb{R}~|~\exist~ x\in D_f\land y=f(x)\}*
Examples:
- The function *f(x)=x^2* has a range of *R_f=\{x~|~x≥0\}* because a number squared is always non-negative.
- The function *g(x)=-3x+5* has a range of *R_g=\mathbb{R}* because the dependent variable can take on any real number.
Graphs of real valued functions
Real functions of a real variable can be graphically represented on a plane with a Cartesian coordinate system. The domain is considered along the abscissa axis (horizontal), and the range along the ordinate axis (vertical). Since both axes are composed of real numbers, the plane is referred to as *\mathbb{R}\times \mathbb{R}* or abbreviated as *\mathbb{R}^2.*
The graphical representation of a function f is given by the points *(x;y)* in the plane where x is in the domain of the function, and *y=f(x).* In other words, the graph of a function is the set of points whose first coordinate is an element of the domain, and the second coordinate is the corresponding image. The graph is denoted as *G_f.*
*G_f=\{(x;y)\in \mathbb{R}^2~|~x\in D_f\land y=f(x)\}*
The graph provides a useful idea of the behavior of a function, and it also helps in understanding abstract concepts. Since the y-coordinate of any point on the graph is *y=f(x)*, you can read the value of *f(x)* directly from the graph. Additionally, the domain and range of the function can be extracted from the graph.
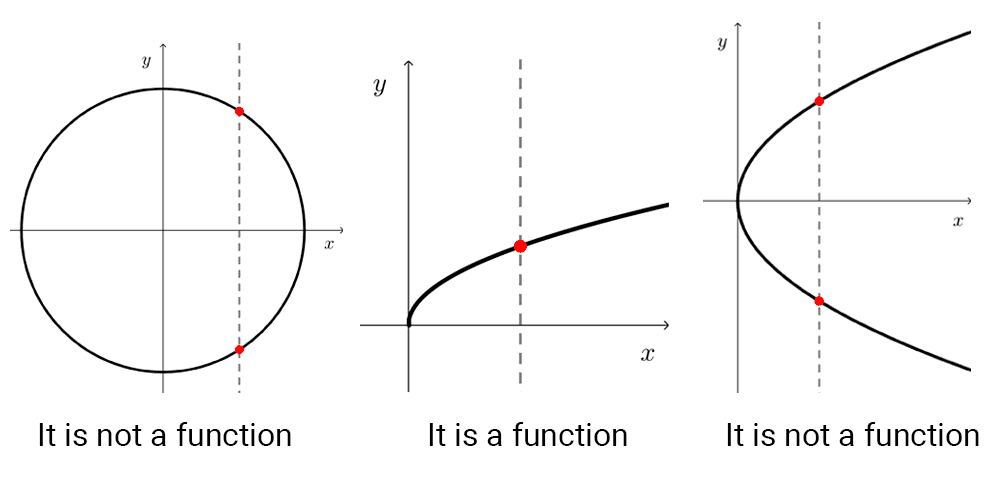
Typically, the graph of a function is a curve in the Cartesian plane, but not all curves in the plane are graphs of functions. The graphs of functions have the property that a vertical line can intersect them at most in one point because otherwise, it would mean that the same number has more than one image, not meeting the definition of a function.
This principle is used to verify whether a curve is the graph of a function or not and is known as the vertical line test.
When constructing the graph of any function, it is useful to find, if they exist, the intersections of the graph with the coordinate axes.
The intersection with the y-axis, if it exists, is unique and is obtained for *x=0.* In other words, if there is an intersection point of the graph with the ordinate axis, that point is *(0;f(0)).*
The intersections with the x-axis, if they exist, correspond to the points where the value of the function is zero. The points in the domain where this happens are called zeros of the function. In other words, the real number *a* is a zero of the function if *f(a)=0,* and the graph of f intersects the x-axis at the point *(a;0).*
According to the graph, *a_1* and *a_2* are zeros of the function f.
Examples of real valued functions and their graphs
We will see below some examples of basic real functions together with their graphical representation.
Linear functions
Linear functions are those of the form *f(x)=mx+b* where m and b are real numbers. The domain of these functions is the set of real numbers, *\mathbb{R}.*
Examples:
*f(x) = x*
*f(x) = 2x + 1*
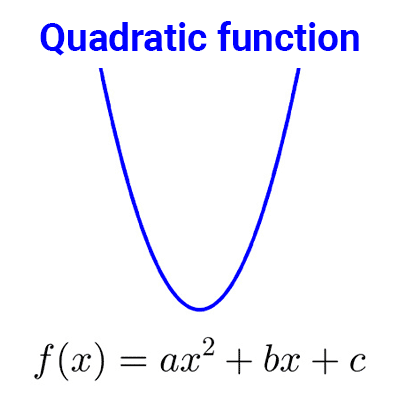
Quadratic functions
Quadratic functions are those of the form *f(x) = ax^2 + bx + c* where a, b, and c are real numbers, and *a≠0.* The domain of these functions is the set of real numbers, *\mathbb{R}.*
Examples:
*f(x)=x^2*
*g(x)=-x^2+5*
Cubic functions
Cubic functions are those of the form *f(x) = ax^3 + bx^2 + cx + d* where a, b, c, d are real numbers, and *a≠0.* The domain of these functions is the set of real numbers, *\mathbb{R}.*
Examples:
*f(x)=x^3*
*f(x) = -x^3 + 2x^2 + 1*
Rational functions
Rational functions are those of the form *f(x) = \dfrac{p(x)}{q(x)}* where p and q are polynomial functions, that is, of the form:
*p(x)=a_mx^m + a_{m-1}x^{m-1} + ... + a_1x + a_0*
*q(x)=b_nx^n + b_{n-1}x^{n-1} + ... + b_1x + b_0*
where *a_0, a_1, ..., a_m~* and *~b_0, b_1, ..., b_n* are real numbers; *m* and *n* are natural numbers.
The domain of rational functions is the set of all real numbers except those that make the denominator *q(x)* equal to zero.
*D_f=\mathbb{R}-\{x~|~q(x)=0\}*
Examples:
*f(x)=\dfrac{1}{x}*
*g(x) = \dfrac{x^2}{1-x}*
Square root function
The square root function is *f(x) = \sqrt{x}.* Its domain and range are the set of non-negative real numbers.
Absolute value function
The absolute value function is *f(x)=|x|.* Its domain is the set of real numbers, and its range is the set of non-negative real numbers.
FAQs
What is a real valued function?
A real valued function is a mathematical rule that assigns to each real number in its domain exactly one real number in its codomain. In other words, for each input value (independent variable) in the function's domain, there is exactly one corresponding value in the range (dependent variable).
How do you prove a function is real-valued?
To demonstrate that a function is real, it must be shown that the rule of correspondence between the elements of the domain and the range is well-defined and satisfies the condition of assigning a unique value in the range for each value in the domain. Additionally, both the domain and the range should be subsets of real numbers.
What is the symbol for a real-valued function?
The symbolism used to denote real functions is f: A → R where A is a subset of real numbers and R is the set of real numbers.
What are the properties of a real-valued function?
Real functions can have various properties such as continuity, differentiability, integrability, monotonicity, boundedness, among others. These properties depend on the specific nature of the function and its behavior in its domain.
Is every function a real-valued function?
No, not all functions are real functions. There are different types of functions, such as complex functions that assign complex numbers as values, vector functions that assign vectors as values, among others.
Do all real-valued functions have an inverse?
No, not all real functions have inverses. For a function to have an inverse, it must be bijective, meaning it must be both injective (each element of the domain is mapped to a unique element of the range) and surjective (every element of the range is reached at least once). Not all real functions meet these conditions.
What are the types of real-valued function?
Real-valued functions can be classified into two main categories:
1. Algebraic Functions: These functions can be expressed using basic algebraic operations such as addition, subtraction, multiplication, division, exponentiation, and roots of polynomials. Notable examples include polynomial functions and rational functions.
2. Transcendental Functions: This group encompasses functions that cannot be represented by a finite number of algebraic operations. It includes functions like exponentials, logarithmic, trigonometric, and hyperbolic functions, as well as combinations of these.
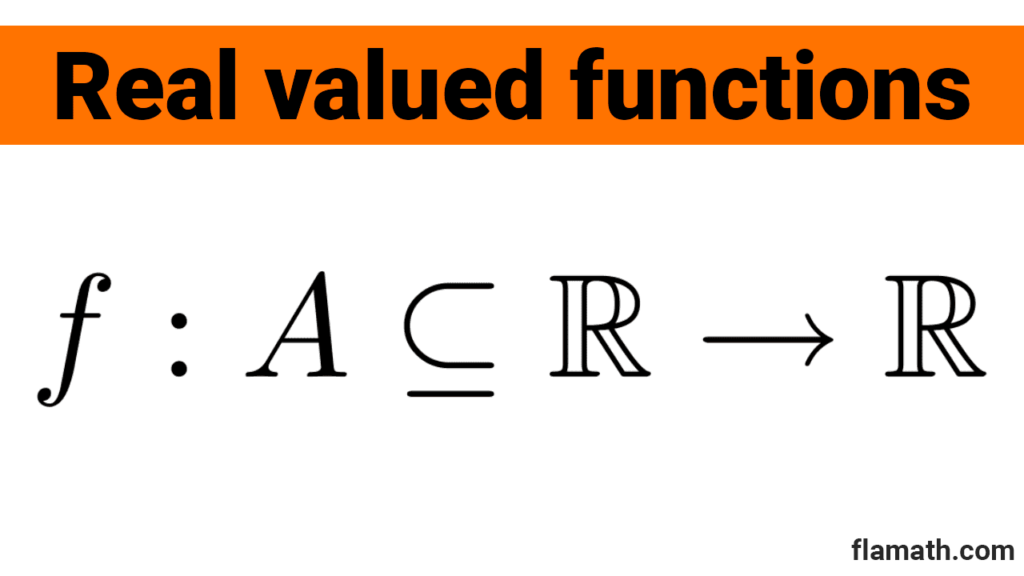


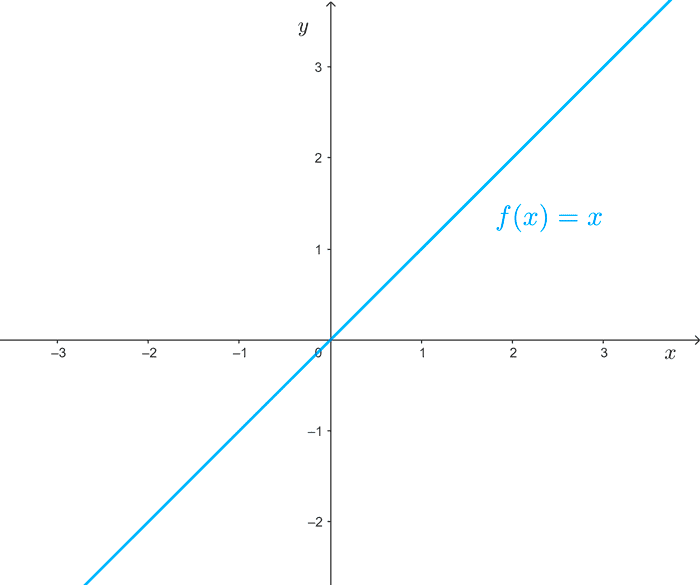


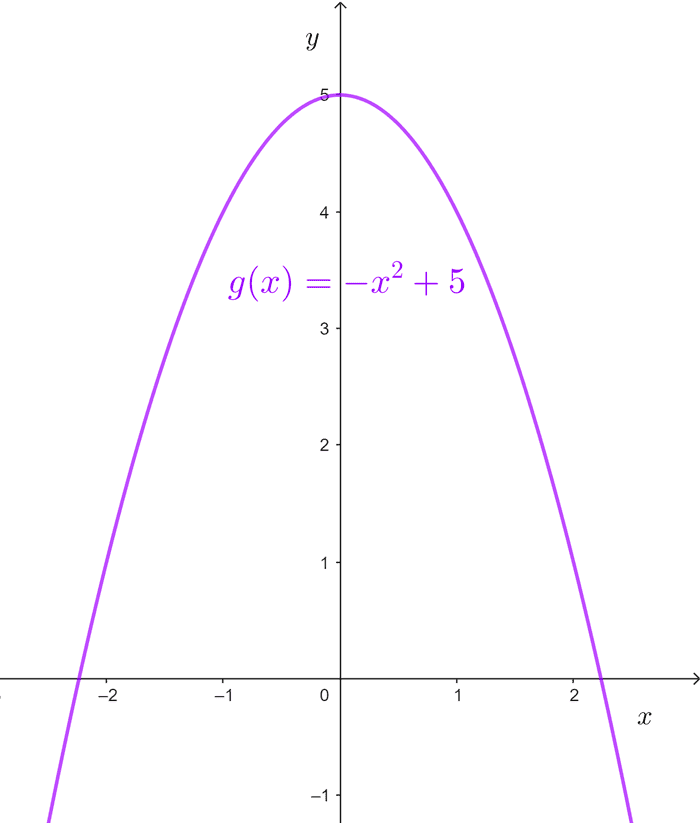
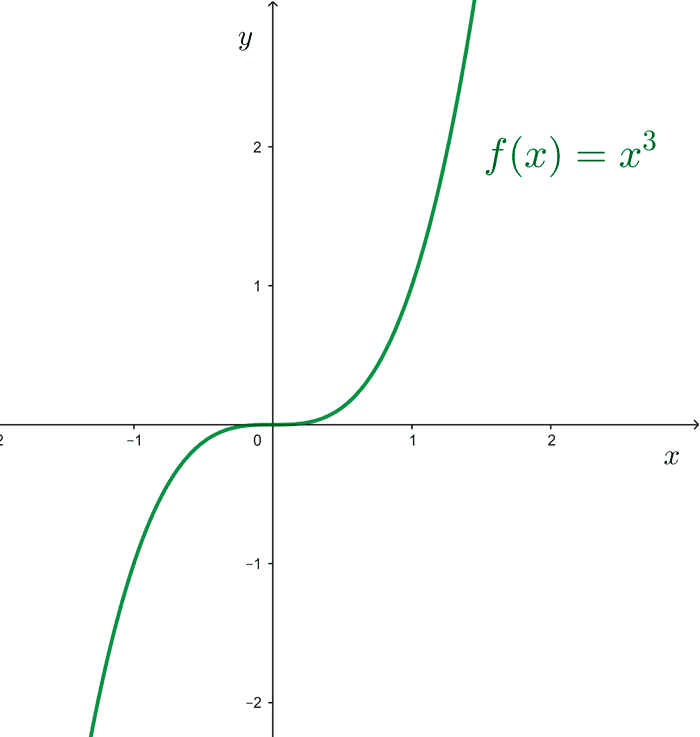
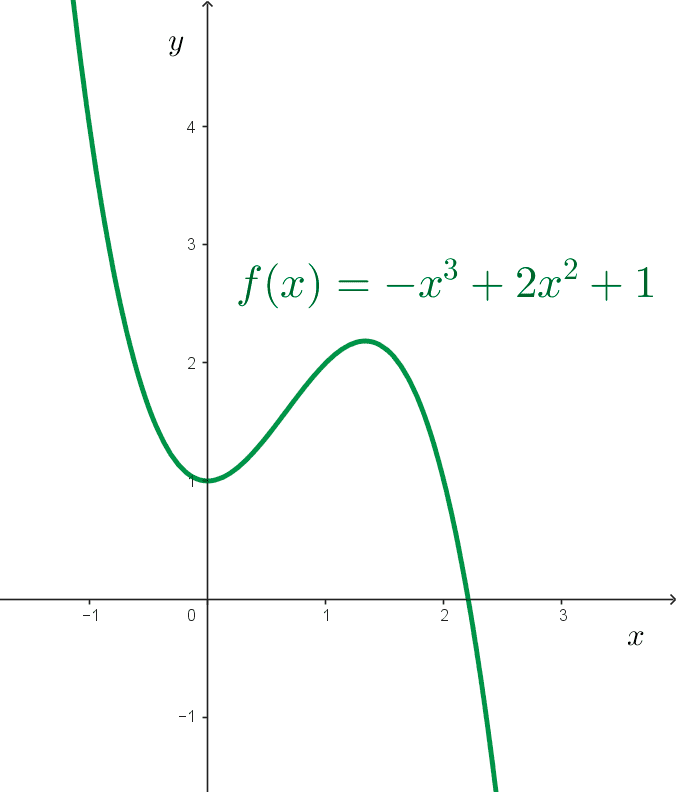




Other articles that may interest you