Equal sets

In this article we explain what is set equality in discrete mathematics set theory and look at examples and properties of this relation.

When are two sets equal?

Two sets are equal if they have exactly the same elements regardless of the order in which they appear or if they are repeated. The equality relationship is symbolized by "=". Thus, if A and B are two equal sets, it is written as A=B. 

One way to determine if two sets are equal is to check if they include each other. This comes from the antisymmetry property of set inclusion:

*A=B* if and only if *A⊆B* and *B⊆A*

Two sets are not equal if one contains at least one element that the other set does not contain, and the symbol "≠" is used. So, if A and B are different, it is written as A≠B.

Unlike equivalence, where the sets must only have the same cardinal, to be equal the sets must have the same cardinal and also the same elements.

Examples

1. The set A = {1, 2, 3} is equal to set B = {3, 1, 2} because both have the same elements, even though they are in a different order, so A = B.
2. The set C = {a, b, c, c, b} and set D = {b, a, a, b, c} are equal, since they both have the same elements, even if they appear in a different order or are repeated.
3. The set E = {-1, 0, 1} is different from set F = {1, 2, 4}, because the elements "-1" and "0" are in E but not in F, and vice versa, "2" and "4" are in F but not in E. So, E ≠ F.
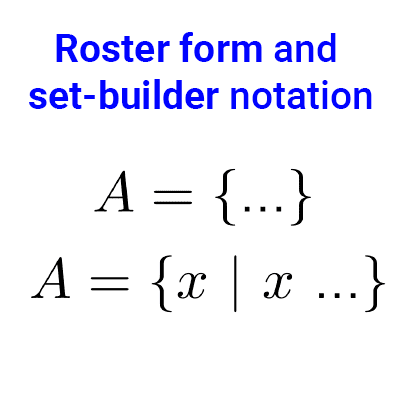
4. The set M = {-2, 2} is equal to set N = {x | *x^2=4*}, because we can write N in extension as N={-2, 2} and conclude that M = N.
5. The infinite set of positive integers Z⁺= {1, 2, 3, 4,...} is equal to the set of natural numbers N = {1, 2, 3, 4,...} because they both have the same elements, so Z⁺=N.
6. The set of real numbers R is different from the set of rational numbers Q, because there are real numbers that are not rational, but are irrational (like *π,* *e,* *\sqrt{2},* etc). So, *\mathbb{R}\neq \mathbb{Q}.*

Properties of equality

The equality relationship of sets satisfies the following properties.

• Reflexivity: every set is equal to itself. That is, A=A for any set A.
• Symmetry: if one set is equal to another, then the second set is also equal to the first. That is, if A=B, then B=A.
• Transitivity: if one set is equal to another and the second set is equal to a third, then the first set is equal to the third. That is, if A=B and B=C, then A=C.

Practice exercises