Ordering fractions

In this article we explain how to order fractions in ascending or descending order. We will see solved examples step by step.

Order of fractions

In rational numbers, there exists an order relationship so that, if we have two fractions, we can determine which one is greater (if they are not equal).

How to order fractions

To achieve fraction ordering, we have two possible approaches: to analyze the fraction directly or to find the corresponding decimal expressions and compare them. We will focus on doing the former.

If you are working with negative fractions, the criteria change. Additionally, we can add that every positive fraction is greater than a negative fraction. 

When two fractions have different denominators and numerators, you can find equivalent fractions with the same denominator and compare the numerators.

Same denominator fractions

If two positive fractions have the same denominator, the one with the greater numerator is larger. 

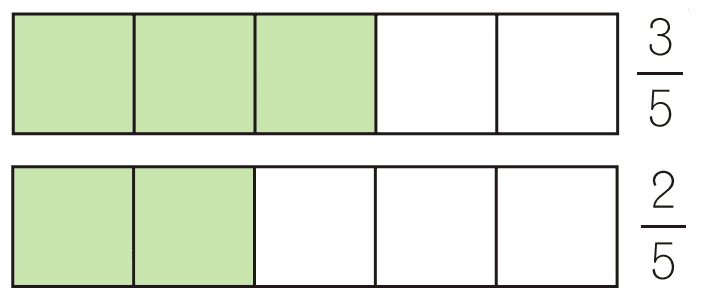
Example 1: comparing the fractions *\dfrac{3}{5}* and *\dfrac{2}{5}*

Both fractions have the same denominator and are proper, so the one with the greater numerator will be larger: 

*\dfrac{3}{5}>\dfrac{2}{5}* because *3>2*

Example 2: order the fractions from least to greatest: *\dfrac{17}{8},* *\dfrac{2}{8}* and *\dfrac{5}{8}.*

All three fractions are homogeneous, so the one with the smallest numerator will be smaller, and the one with the largest numerator will be larger, resulting in the following order:

*\dfrac{2}{8}<\dfrac{5}{8}<\dfrac{17}{8}* because *2<5<17*

It could also be deduced that the last one is the largest because it is an improper fraction, and the others are proper.

If two negative fractions have the same denominator, the one with the smaller numerator is larger.

Example: order the fractions from greatest to least: *-\dfrac{5}{7},* *-\dfrac{8}{7}* and *-\dfrac{27}{7}*

Fractions closer to zero will be larger than the others, keeping this in mind, we apply the rule and arrive at:

*-\dfrac{5}{7}>-\dfrac{8}{7}>-\dfrac{27}{7}*

because *5<8<27* (or *-5>-8>-27*)

If we need to order positive and negative fractions, we do the corresponding ordering within each group, remembering that negative fractions are always smaller than positive ones.

Example: order the fractions from least to greatest *\dfrac{5}{2},* *-\dfrac{5}{2},* *\dfrac{14}{2},* and *-\dfrac{1}{2}*

In the negative group: *-\dfrac{5}{2}<-\dfrac{1}{2}* because *5>1*

In the positive group: *\dfrac{5}{2}<\dfrac{14}{2}* because *14>5*

Combining the information, we can order them all as follows:

*-\dfrac{5}{2}<-\dfrac{1}{2}<\dfrac{5}{2}<\dfrac{14}{2}*

Same numerator fractions

When two positive fractions have the same numerator, the one with the smaller denominator is greater. 

Example: order from greatest to least the fractions *\dfrac{2}{17},* *\dfrac{2}{8}* and *\dfrac{2}{5}.*

Applying the rule:

*\dfrac{2}{5}>\dfrac{2}{8}>\dfrac{2}{17}* because *5<8<17*

The rule follows the logic that if we take the same number of parts of a whole, we will have more when the whole is divided into fewer parts. For example: if we can eat two slices of a pizza, we will eat more pizza when it is divided into 4 slices than when it is divided into 8. 

When two negative fractions have the same numerator, the one with the larger denominator is greater.

Example: order from least to greatest the fractions *-\dfrac{2}{17},* *-\dfrac{2}{5}* and *-\dfrac{2}{8}*

Solution: *-\dfrac{2}{5}<-\dfrac{2}{8}<-\dfrac{2}{17}* because *17>8>5*

Fractions of different numerator and denominator

Example 1: order from least to greatest the fractions: *\dfrac{7}{3},* *\dfrac{21}{10}* and *\dfrac{11}{15}*

First, break down the denominators to find the least common multiple:

*3=3*

*10=5\cdot 2*

*15=3\cdot 5*

*LCM(3,10,15)=3\cdot 5\cdot 2=30*

The new denominator for the fractions will be *30.* To calculate the numerator for each fraction, divide this number by each denominator, and multiply the result by the numerator.

For example, for *\dfrac{7}{3},* divide 30 by 3: 

*30:3=10*

Then, multiply this result by 7:

*10\cdot 7=70*

So, the new numerator will be 70, resulting in *\dfrac{7}{3}=\dfrac{70}{30}*

For the other fractions:

*30:10=3, 3\cdot 21=63.* So *\dfrac{21}{10}=\dfrac{63}{30}*

*\dfrac{11}{15}=\dfrac{11\cdot 2}{30}=\dfrac{22}{30}*

Now we can compare because the fractions have a common denominator:

*\dfrac{22}{30}<\dfrac{63}{30}<\dfrac{70}{30}* because *22<63<70*

So, replacing the fractions with their original equivalents:

*\dfrac{11}{15}<\dfrac{21}{10}<\dfrac{7}{3}*

Example 2: order *\dfrac{1}{2}, \dfrac{3}{4}, \dfrac{5}{8}* and *\dfrac{7}{10}* in descending order.

Calculate the LCM of the denominators:

*2=2*

*4=2^2*

*8=2^3*

*10=5\cdot 2*

*LCM(2,4,8,10)=2^3\cdot 5=40*

Now, find the equivalent fractions for each of the original ones.

*\dfrac{1}{2}=\dfrac{1\cdot 20}{40}=\dfrac{20}{40}*

*\dfrac{3}{4}=\dfrac{3\cdot 10}{40}=\dfrac{30}{40}*

*\dfrac{5}{8}=\dfrac{5\cdot 5}{40}=\dfrac{25}{40}*

*\dfrac{7}{10}=\dfrac{7\cdot 4}{40}=\dfrac{28}{40}*

With all the fractions having the same denominator, we can order them from greatest to least:

*\dfrac{30}{40}>\dfrac{28}{40}>\dfrac{25}{40}>\dfrac{20}{40}* because *30>28>25>20*

Replacing with the original fractions:

*\dfrac{3}{4}>\dfrac{7}{10}>\dfrac{5}{8}>\dfrac{1}{2}*