
Radicals mixed operations
In this article we explain how to solve combined operations with roots. We will see a step-by-step guide with solved exercises.
Table of Contents
What are combined operations with radicals
Combined or mixed operations with radicals are expressions involving sums, subtractions, multiplications, and divisions where roots appear. To solve them, it is necessary to know how to proceed in each case. Here you can read the specific step-by-step process for each operation:
How to solve combined operations with radicals
Some recommendations for solving these types of problems are:
- Simplify each radical as much as possible, even before starting the operations. This will allow you to work with less complex expressions.
- Understand the properties of roots such as the square root of a product, square root of a quotient, and square root of a root. This will facilitate the operation process.
It is convenient to follow a certain order of operations to avoid reaching incorrect results. This order is often referred to as the order of operations.
The order of operations to solve combined operations is:
- First, solve what is inside parentheses, brackets, and braces.
- Solve exponents and roots (when possible).
- Solve multiplication and division.
- Calculate addition and subtraction.
This order is not strict, and in most cases, the same problem can be solved using different procedures. However, following the order of operations can be useful.
Example 1
*\dfrac{\sqrt{2}\sqrt[3]{3}}{\sqrt{5}}*
In the exercise, both division and multiplication appear. They have the same order of operations, but it is convenient to first solve the product in the numerator and then the division.
To solve multiplications and divisions of radicals, the radicals must have the same index. We could first do this in the denominator and then, the result, equalize the denominator, but to simplify the calculations, we find a common index for the three roots.
*LCM(2,3,2)=6*
For *\sqrt{2}:*
*\dfrac{6}{2}=3*
Then: *\sqrt{2}=\sqrt[2\cdot 3]{2^{3}}=\sqrt[6]{8}*
For *\sqrt[3]{3}:*
*\dfrac{6}{3}=2*
Then: *\sqrt[3]{3}=\sqrt[3\cdot 2]{3^2}=\sqrt[6]{9}*
For *\sqrt{5}:*
*\dfrac{6}{2}=3*
Then: *\sqrt{5}=\sqrt[2\cdot 3]{5^3}=\sqrt[6]{125}*
Having equalized, we can proceed to solve the exercise:
*\dfrac{\sqrt{2}\sqrt[3]{3}}{\sqrt{5}}=\dfrac{\sqrt[6]{8}\sqrt[6]{9}}{\sqrt[6]{125}}*
*=\dfrac{\sqrt[6]{8\cdot 9}}{\sqrt[6]{125}}*
*=\dfrac{\sqrt[6]{72}}{\sqrt[6]{125}}*
*=\sqrt[6]{\dfrac{72}{125}}*
Example 2
*5\sqrt{3}\cdot(9\sqrt{2}+7\sqrt{18})*
In this problem, there is a product and a sum enclosed in parentheses. According to the order of operations, we should first solve the expression inside the parentheses and then multiply. Given the situation, it is also possible to apply the distributive property and arrive at a correct result.
Solving by the order of operations:
*5\sqrt{3}\cdot(9\sqrt{2}+7\sqrt{18})=5\sqrt{3}\cdot(9\sqrt{2}+7\sqrt{3^2\cdot 2})*
*=5\sqrt{3}\cdot(9\sqrt{2}+21\sqrt{2})*
*=5\sqrt{3}\cdot(30\sqrt{2})*
*=5\cdot 30\sqrt{3}{\sqrt{2}}*
*=150\sqrt{6}*
Solving by the distributive property:
*5\sqrt{3}\cdot(9\sqrt{2}+7\sqrt{18})=5\sqrt{3}\cdot 9\sqrt{2}+5\sqrt{3}\cdot 7\sqrt{3^2\cdot 2}*
*=45\sqrt{6}+105\sqrt{6}*
*=150\sqrt{6}*
Example 3
*\dfrac{6\sqrt{3}}{\sqrt[3]{6}}-\sqrt[6]{\dfrac{3}{4}}*
According to the order of operations, we first solve the division and then the subtraction. It is necessary to reduce to a common index.
*LCM(2,3)=6*
*\sqrt{3}=\sqrt[2\cdot 3]{3^3}=\sqrt[6]{27}*
*\sqrt[3]{6}=\sqrt[3\cdot 2]{6^2}=\sqrt[6]{36}*
Replacing in the original problem:
*\dfrac{6\sqrt{3}}{\sqrt[3]{6}}-\sqrt[6]{\dfrac{3}{4}}=\dfrac{6\sqrt[6]{27}}{\sqrt[6]{36}}-\sqrt[6]{\dfrac{3}{4}}*
*=6\sqrt[6]{\dfrac{27}{36}}-\sqrt[6]{\dfrac{3}{4}}*
*=6\sqrt[6]{\dfrac{3}{4}}-\sqrt[6]{\dfrac{3}{4}}*
*=5\sqrt[6]{\dfrac{3}{4}}*
Example 4
*\sqrt{2}\sqrt{8}-(7\sqrt{5}+2\sqrt{3}):(4\sqrt{3})*
In this example, there are root multiplications, addition, subtraction, and division. What is in the first parenthesis cannot be further simplified, and what is in the second parenthesis is the divisor of the operation. To start, we can solve the first multiplication:
*\sqrt{2}\sqrt{8}-(7\sqrt{5}+2\sqrt{3}):(4\sqrt{3})=\sqrt{2\cdot 8}-(7\sqrt{5}+2\sqrt{3}):(4\sqrt{3})*
*=\sqrt{16}-(7\sqrt{5}+2\sqrt{3}):(4\sqrt{3})*
*=4-(7\sqrt{5}+2\sqrt{3}):(4\sqrt{3})*
For convenience, we will rewrite the division with a fractional dash. Then, we distribute the denominator to each term. Because of the negative sign in front, the signs of the two terms will be changed.
*4-(7\sqrt{5}+2\sqrt{3}):(4\sqrt{3})=4-\dfrac{7\sqrt{5}+2\sqrt{3}}{4\sqrt{3}}*
*=4-\dfrac{7\sqrt{5}}{4\sqrt{3}}-\dfrac{2\sqrt{3}}{4\sqrt{3}}*
*=4-\dfrac{7}{4}\sqrt{\dfrac{5}{3}}-\dfrac{1}{2}*
*=\dfrac{7}{2}-\dfrac{7}{4}\sqrt{\dfrac{5}{3}}*
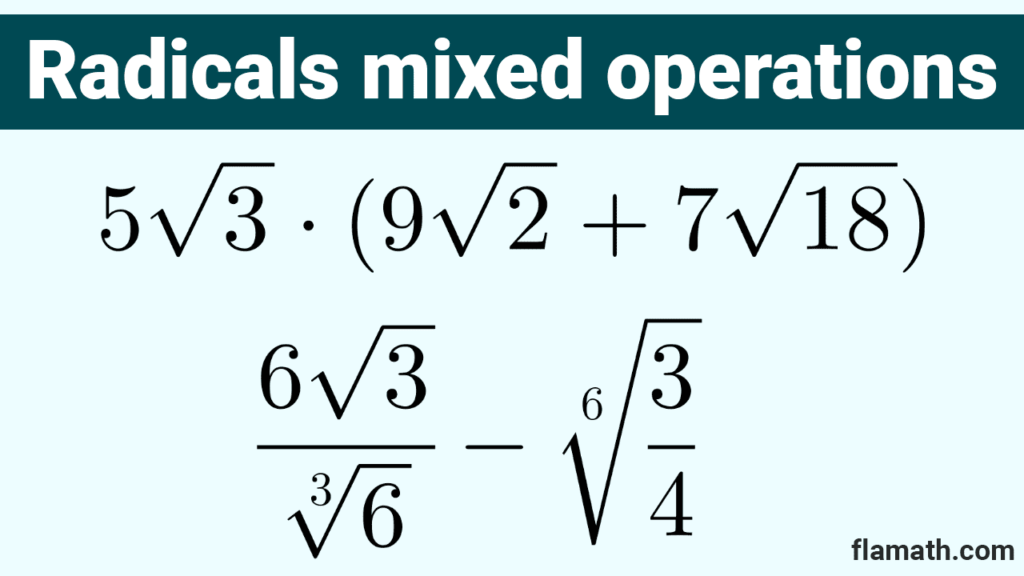


Other articles that may interest you