Types of sets in Math
In this article we explain all the different kinds of sets that exist in discrete mathematics set theory with examples of each.
Table of Contents
Finite set
A finite set is one that has a limited number of elements.
Examples
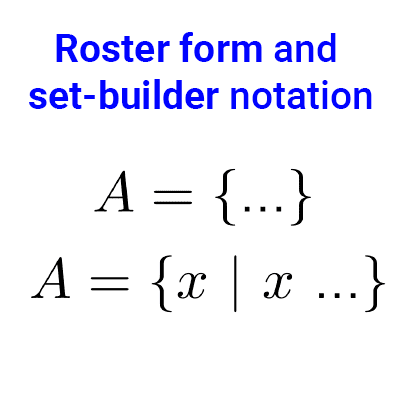
- A = {a, e, i, o, u}
- B = {x | x is a vowel}
Infinite set
An infinite set is one that has an unlimited number of elements.
Examples
- The set of natural numbers N = {1, 2, 3, ...}.
- The set of even integers P = {x | x is even}
Empty set
The empty set, represented by { } or Ø, is one that has no elements.
Examples
- The set of planets orbiting around the moon is Ø
- The set of solutions to the equation *x\cdot 0=4* is empty: Ø={x | *x\cdot 0=4*}
Singleton set
A singleton set is one that contains a single element.
Examples
- The set A={z} is singleton.
- The set of solutions to the equation *2x=4* is singleton: {x | *2x=4*}={2}
Universal set
The universal set is one that contains all the relevant elements for a given context.
Examples:
- When working with natural numbers, the universal set is that of all natural numbers: N.
- When working with triangles, the universal set is that of all triangles.
Complementary set
The complement of a set A, symbolized as A', is the set of all elements that are in the universal set but not in A.
Examples
- The complement of the set of odd integers is the set of even integers.
- The complement of the set of equilateral triangles is the set of triangles that are not equilateral (isosceles and scalene).
Power set
The power set or power set of a set is the set that contains all possible subsets of that original set.
Examples
- The power set of A = {a, b} is P(A) = {Ø, {a}, {b}, {a, b}}.
- The power set of Ø is P(Ø)={Ø}.
Numeric sets
Numeric sets are sets that contain numbers with certain common characteristics.
Examples
- Natural numbers (N)
- Integers (Z)
- Rational numbers (Q)
- Irrational numbers (I)
- Real numbers (R)
- Complex numbers (C)
Subset
A set A is a subset of another set B if all the elements of A are also in B.
Examples
- Set A = {dog, cat} is a subset of B = {dog, cat, bird}.
- The set of natural numbers N is a subset of the integers Z.
Proper subset
A set A is a proper subset of B if all the elements in A are also in B but A≠B.
Examples
- A = {1, 2} is a proper subset of B = {1, 2, 3}.
- The set of even integers is a proper subset of the integers.
Equivalent sets
Two sets are equivalent if they have the same number of elements.
Examples
- The sets A = {a, b, c} and B = {7, 8, 9} are equivalent because they have the same number of elements.
- The set of letters in the word "cat" and the set of integers from 1 to 4 are equivalent because they both have four elements.
Equal sets
Two sets are equal if they have the same elements, regardless of the order.
Examples
- Set A = {a, b, c} is equal to B = {c, b, a}.
- The set {1, -1} is equal to the set {x | x^2=1}
Disjoint sets
Two sets are disjoint if they do not share any common elements.
Examples
- Sets A = {1, 2} and B = {3, 4} are disjoint because they do not share any elements.
- The set of positive real numbers and the set of negative real numbers are disjoint, because there is no number that is both positive and negative at the same time.
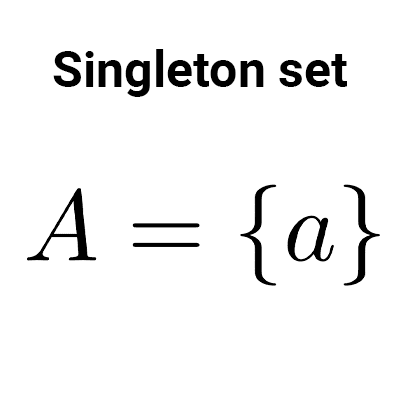
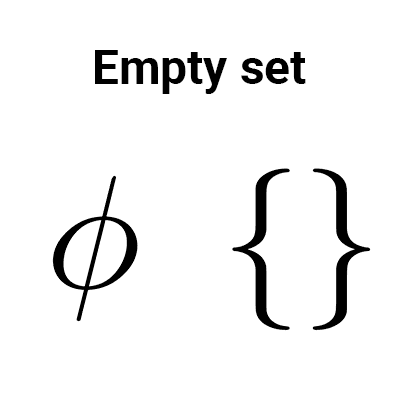
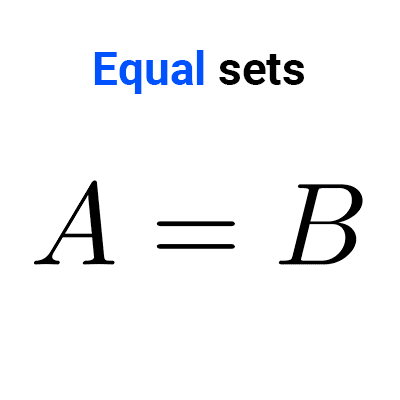

Other articles that may interest you