
Limits of radical functions and indeterminate forms
In this article, we develop the limits of radical functions at a point, as well as at positive and negative infinity. We begin by examining the cases of square and cubic radical functions, and then extend our analysis to the nth root. We also address situations involving indeterminate forms with radical functions.
Let's recall that a radical function is a real function of the form *f(x)=\sqrt[n]{x}*, where n is a positive integer. Its domain depends on the value of n: if n is even, the domain includes non-negative real numbers; if n is odd, the domain includes all real numbers.
Table of Contents
Limits of square root function
The limit of the square root function at a point is equal to the value of the function at that point, provided it is defined there.
*\lim_{x\to a}\sqrt{x}=\sqrt{a}*
Examples:
*\lim_{x\to 4}\sqrt{x}=\sqrt{4}=2*
*\lim_{x\to 10}\sqrt{x}=\sqrt{10}*
The limit of the square root function at positive infinity is equal to positive infinity. The limit at negative infinity does not exist.
*\lim_{x\to \infty}\sqrt{x}=+\infty*
*\lim_{x\to -\infty}\sqrt{x}* does not exist.
When dealing with a composite function involving the square root function, we can use the theorem of the limit of composite functions, as the required conditions for using this theorem are satisfied.
The limit of the square root of a function at a point is equal to the square root of the limit of the function at that point, provided the limit exists and is non-negative.
*\lim_{x\to a}\sqrt{g(x)}=\sqrt{\lim_{x\to a} g(x)}*
as long as *\lim_{x\to a} g(x)* exists and is positive or zero.
Examples:
*\lim_{x\to 2}\sqrt{7+x}=\sqrt{\lim_{x\to 2} (7+x)}=\sqrt{7+2}=\sqrt{9}=\sqrt{3}*
*\lim_{x\to 1}\sqrt{x^2+1}=\sqrt{\lim_{x\to 1} (x^2+1)}=\sqrt{(1)^2+1}=\sqrt{2}*
Limits of cube root function
The limit of the cubic root function at a point is equal to the value of the function at that point.
*\lim_{x\to a}\sqrt[3]{x}=\sqrt[3]{a}*
Examples:
*\lim_{x\to 8}\sqrt[3]{x}=\sqrt[3]{8}=2*
*\lim_{x\to -27}\sqrt[3]{x}=\sqrt[3]{-27}=-3*
The limit of the cubic root function at positive infinity is equal to positive infinity. The limit at negative infinity is equal to negative infinity.
*\lim_{x\to \infty}\sqrt[3]{x}=+\infty*
*\lim_{x\to -\infty}\sqrt[3]{x}=-\infty*
Just like with the square root, we can apply the theorem of the limit of composite functions when dealing with a composition involving a cubic root.
The limit of the cubic root of a function at a point is equal to the cubic root of the limit of the function at that point, provided the limit exists.
*\lim_{x\to a}\sqrt[3]{g(x)}=\sqrt[3]{\lim_{x\to a} g(x)}*
Note that we do not apply the restriction that the radicand must be positive because cubic roots of negative numbers are indeed real numbers.
Examples:
*\lim_{x\to 5}\sqrt[3]{x^2-1}=\sqrt[3]{\lim_{x\to 5} (x^2-1)}=\sqrt[3]{5^2-1}=\sqrt[3]{24}*
*\lim_{x\to 3}\sqrt[3]{2^x}=\sqrt[3]{\lim_{x\to 3} 2^x}=\sqrt[3]{2^3}=2*
Limits of nth root function
Taking a general case, if *f(x)=\sqrt[n]{x},* where n is a positive integer, the limit of the nth root function at a point is equal to the value of the function at that point, provided the radicand is positive if n is even.
*\lim_{x\to a}\sqrt[n]{x}=\sqrt[n]{a}*
provided that a is positive if n is even.
Examples:
*\lim_{x\to 81}\sqrt[4]{x}=\sqrt[4]{81}=3*
*\lim_{x\to 3}\sqrt[6]{x}=\sqrt[6]{3}*
The limit of the nth root function at positive infinity is equal to positive infinity.
*\lim_{x\to \infty}\sqrt[n]{x}=+\infty*
The limit at negative infinity is equal to negative infinity (if n is odd) and does not exist if n is even.
- If n is odd, then *\lim_{x\to -\infty}\sqrt{x}=-\infty*
- If n is even, then *\lim_{x\to -\infty}\sqrt{x}* does not exist.
We can apply the theorem of the limit of a composite function in the case of the nth root, as long as we demand that the conditions be met. In this case, it will suffice to require that the radicand is not negative when the root index is even.
The limit of the nth root of a function at a point is equal to the nth root of the limit of the function at that point, provided the limit exists and is positive if n is even.
*\lim_{x\to a}\sqrt[n]{g(x)}=\sqrt[n]{\lim_{x\to a} g(x)}*
Examples:
*\lim_{x\to -1}\sqrt[3]{-x-8}=\sqrt[3]{\lim_{x\to -1} (-x-8)}=\sqrt[3]{-1-8}=\sqrt[3]{-9}*
*\lim_{x\to 7}\sqrt[10]{x^3-10}=\sqrt[10]{\lim_{x\to 7} (x^3-10)}=\sqrt[10]{7^3-10}=\sqrt[10]{333}*
Indeterminate forms with radical functions
We will see below some examples of how to solve different indeterminate forms involving functions with roots.
Indeterminate form zero over zero (0/0)
Example 1: *\lim_{x\to 4} \dfrac{\sqrt{x}-2}{x-4}*
Solution: To resolve the indeterminate form 0/0, we can multiply and divide the function by the conjugate of the part with a radical, allowing us to apply a difference of squares in the numerator.
*\lim_{x\to 4} \dfrac{\sqrt{x}-2}{x-4}=\lim_{x\to 4} \left(\dfrac{\sqrt{x}-2}{x-4}\cdot \dfrac{\sqrt{x}+2}{\sqrt{x}+2}\right)*
*=\lim_{x\to 4} \dfrac{(\sqrt{x})^2-(2)^2}{(x-4)(\sqrt{x}+2)}*
*=\lim_{x\to 4} \dfrac{x-4}{(x-4)(\sqrt{x}+2)}*
*=\lim_{x\to 4} \dfrac{\cancel{x-4}}{\cancel{(x-4)}(\sqrt{x}+2)}*
*=\lim_{x\to 4} \dfrac{1}{\sqrt{x}+2}*
Now we can calculate the limit, and it will not be indeterminate:
*\lim_{x\to 4} \dfrac{\sqrt{x}-2}{x-4}=\lim_{x\to 4} \dfrac{1}{\sqrt{x}+2}*
*=\dfrac{1}{\sqrt{4}+2}*
*=\dfrac{1}{2+2}*
*=\dfrac{1}{4}*
Example 2: *\lim_{x\to 2} \dfrac{x-\sqrt{x+2}}{\sqrt{4x+1}-3}*
Solution: We can apply the same procedure as before but multiplying and dividing by the conjugates of the numerator and denominator, as both have radicals.
*\lim_{x\to 2} \dfrac{x-\sqrt{x+2}}{\sqrt{4x+1}-3}=*
*=\lim_{x\to 2} \dfrac{x-\sqrt{x+2}}{\sqrt{4x+1}-3}\cdot \dfrac{x+\sqrt{x+2}}{x+\sqrt{x+2}}\cdot \dfrac{\sqrt{4x+1}+3}{\sqrt{4x+1}+3}*
*=\lim_{x\to 2} \dfrac{(x^2-x-2)(\sqrt{4x+1}+3)}{(4x-8)(x+\sqrt{x+2})}*
*=\lim_{x\to 2} \dfrac{(x^2-x-2)(\sqrt{4x+1}+3)}{4(x-2)(x+\sqrt{x+2})}*
The numerator polynomial *x^2-x-2* can be factored as *x^2-x-2=(x-2)(x+1).* Substituting in the limit:
*\lim_{x\to 2} \dfrac{(x^2-x-2)(\sqrt{4x+1}+3)}{4(x-2)(x+\sqrt{x+2})}*
*=\lim_{x\to 2} \dfrac{(x-2)(x+1)(\sqrt{4x+1}+3)}{4(x-2)(x+\sqrt{x+2})}*
*=\lim_{x\to 2} \dfrac{\cancel{(x-2)}(x+1)(\sqrt{4x+1}+3)}{4\cancel{(x-2)}(x+\sqrt{x+2})}*
*=\lim_{x\to 2} \dfrac{(x+1)(\sqrt{4x+1}+3)}{4(x+\sqrt{x+2})}*
*=\dfrac{(2+1)(\sqrt{4\cdot 2+1}+3)}{4(2+\sqrt{2+2})}*
*=\dfrac{9}{8}*
Indeterminate form infinity over infinity (∞/∞)
Example 1: *\lim_{x\to \infty} \dfrac{\sqrt{x^2+1}}{3x-5}*
Solution: To resolve this indeterminate form, we can divide both the numerator and denominator by the variable raised to the highest power.
*\lim_{x\to \infty} \dfrac{\sqrt{x^2+1}}{3x-5}=\lim_{x\to \infty} \dfrac{\dfrac{\sqrt{x^2+1}}{x}}{\dfrac{3x-5}{x}}*
*=\lim_{x\to \infty} \dfrac{\sqrt{\dfrac{x^2}{x^2}+\dfrac{1}{x^2}}}{\dfrac{3x}{x}-\dfrac{5}{x}}*
*=\lim_{x\to \infty} \dfrac{\sqrt{1+\dfrac{1}{x^2}}}{3-\dfrac{5}{x}}*
*=\dfrac{\sqrt{1+\dfrac{1}{\infty^2}}}{3-\dfrac{5}{\infty}}*
*=\dfrac{\sqrt{1+0}}{3-0}*
*=\dfrac{1}{3}*
Note: for x to enter the square root, it must be squared.
Example 2: *\lim_{x\to \infty} \dfrac{\sqrt{x+3}-2}{x-1}*
Solution: Similarly to the previous case, we divide the numerator and denominator by the variable raised to the power of 1.
*\lim_{x\to \infty} \dfrac{\sqrt{x+3}-2}{x-1}=\lim_{x\to \infty} \dfrac{\dfrac{\sqrt{x+3}-2}{x}}{\dfrac{x-1}{x}}*
*=\lim_{x\to \infty} \dfrac{\sqrt{\dfrac{x}{x^2}+\dfrac{3}{x^2}}-\dfrac{2}{x}}{\dfrac{x}{x}-\dfrac{1}{x}}*
*=\lim_{x\to \infty} \dfrac{\sqrt{\dfrac{1}{x}+\dfrac{3}{x^2}}-\dfrac{2}{x}}{1-\dfrac{1}{x}}*
*=\dfrac{\sqrt{\dfrac{1}{\infty}+\dfrac{3}{\infty^2}}-\dfrac{2}{\infty}}{1-\dfrac{1}{\infty}}*
*=\dfrac{\sqrt{0+0}-0}{1-0}*
*=\dfrac{0}{1}*
*=0*
Indeterminate form infinity minus infinity (∞-∞)
Example 1: *\lim_{x\to \infty} (\sqrt{x^2-2}-\sqrt{x^2+x})*
Solution: A common approach to solving these indeterminations is to transform them into a ∞/∞ type and then solve it. We can do this by multiplying and dividing by the conjugate of the function and then using the difference of squares.
*\lim_{x\to \infty} (\sqrt{x^2-2}-\sqrt{x^2+x})=\lim_{x\to \infty} (\sqrt{x^2-2}-\sqrt{x^2+x})\cdot \dfrac{\sqrt{x^2-2}+\sqrt{x^2+x}}{\sqrt{x^2-2}+\sqrt{x^2+x}}*
*=\lim_{x\to \infty} \dfrac{x^2-2-x^2-x}{\sqrt{x^2-2}+\sqrt{x^2+x}}*
*=\lim_{x\to \infty} \dfrac{-2-x}{\sqrt{x^2-2}+\sqrt{x^2+x}}*
At this point, attempting to solve the limit will yield an indetermination ∞/∞; we can resolve it by dividing both numerator and denominator by the variable raised to the power of 1.
*\lim_{x\to \infty} \dfrac{-2-x}{\sqrt{x^2-2}+\sqrt{x^2+x}}*
*=\lim_{x\to \infty} \dfrac{\dfrac{-2-x}{x}}{\dfrac{\sqrt{x^2-2}+\sqrt{x^2+x}}{x}}*
*=\lim_{x\to \infty} \dfrac{-\dfrac{2}{x}-\dfrac{x}{x}}{\sqrt{\dfrac{x^2}{x^2}-\dfrac{2}{x^2}}+\sqrt{\dfrac{x^2}{x^2}+\dfrac{x}{x^2}}}*
*=\lim_{x\to \infty} \dfrac{-\dfrac{2}{x}-1}{\sqrt{1-\dfrac{2}{x^2}}+\sqrt{1+\dfrac{1}{x}}}*
*=\dfrac{-\dfrac{2}{\infty}-1}{\sqrt{1-\dfrac{2}{\infty^2}}+\sqrt{1+\dfrac{1}{\infty}}}*
*=\dfrac{0-1}{\sqrt{1-0}+\sqrt{1+0}}*
*=-\dfrac{1}{2}*
Example 2: *\lim_{x\to \infty} (x+\sqrt{x}-\sqrt{x-\sqrt{x}})*
Solution: Similarly to the previous case, we multiply and divide by the conjugate of the function and apply a difference of squares.
*\lim_{x\to \infty} (x+\sqrt{x}-\sqrt{x-\sqrt{x}})=\lim_{x\to \infty} (x+\sqrt{x}-\sqrt{x-\sqrt{x}})\cdot \dfrac{x+\sqrt{x}+\sqrt{x-\sqrt{x}}}{x+\sqrt{x}+\sqrt{x-\sqrt{x}}}*
*=\lim_{x\to \infty} \dfrac{(x+\sqrt{x})^2-x-\sqrt{x}}{x+\sqrt{x}+\sqrt{x+\sqrt{x}}}*
*=\lim_{x\to \infty} \dfrac{x^2+2x\sqrt{x}+x-x-\sqrt{x}}{x+\sqrt{x}+\sqrt{x+\sqrt{x}}}*
*=\lim_{x\to \infty} \dfrac{x^2+2x\sqrt{x}-\sqrt{x}}{x+\sqrt{x}+\sqrt{x+\sqrt{x}}}*
Now, it's an indeterminate form of infinity over infinity that we can resolve by dividing the numerator and denominator by the variable raised to the highest power, in this case, 2.
*\lim_{x\to \infty} \dfrac{x^2+2x\sqrt{x}-\sqrt{x}}{x+\sqrt{x}+\sqrt{x+\sqrt{x}}}*
*=\lim_{x\to \infty} \dfrac{\dfrac{x^2}{x^2}+\dfrac{2x\sqrt{x}}{x^2}-\dfrac{\sqrt{x}}{x^2}}{\dfrac{x}{x^2}+\dfrac{\sqrt{x}}{x^2}+\dfrac{\sqrt{x+\sqrt{x}}}{x^2}}*
*=\lim_{x\to \infty} \dfrac{1+\dfrac{2}{\sqrt{x}}+\dfrac{1}{x^{3/2}}}{\dfrac{1}{x}+\dfrac{1}{x^{3/2}}+\sqrt{\dfrac{1}{x^2}-\dfrac{1}{x^{7/2}}}}*
*=\dfrac{1+0+0}{0}*
*=\infty*


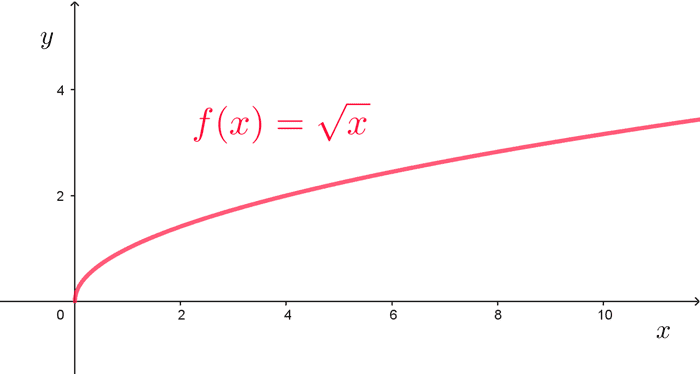
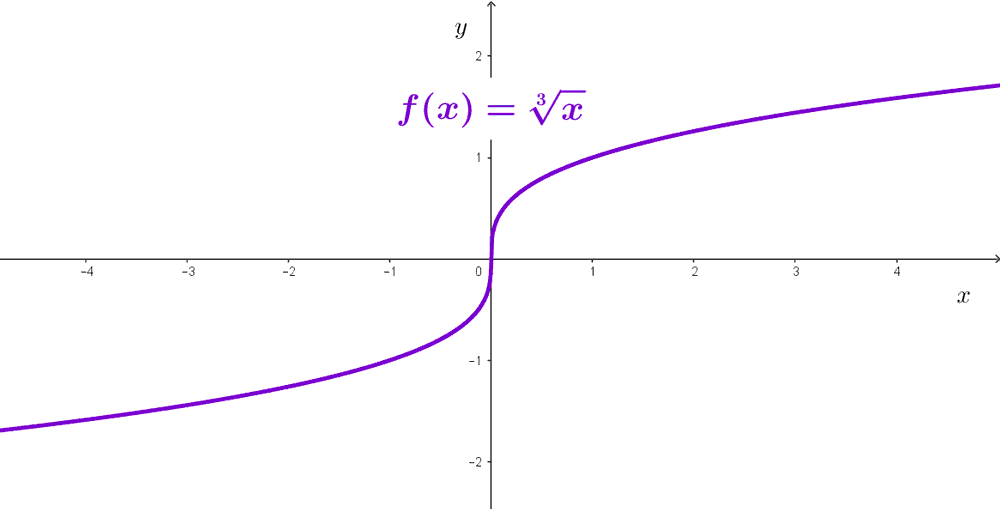
Other articles that may interest you