Domain of a function

In this article we explain what is the domain of a function, how it is interpreted graphically and examples of common function domains.

What is the domain?

The domain of a function is the set of values that the independent variable can take, i.e., those for which there exists an image. The domain is also called the domain of existence or the set of departure. It is symbolized by the letter D and sometimes with the name of the function as a subscript.

In real functions, the domain is a subset of the real numbers. Thus, the domain of a real function f is symbolically defined as:

*D_f=\{x∈\mathbb{R}~|~∃y∈\mathbb{R}~∧~y=f(x)\}*

Recall that a function is a rule that assigns to every element of a set A a unique element of a set B. The set A is called the domain of the function, set B is the codomain, and the range is a subset of B.

The domains of real functions are often expressed in interval notation, unions of intervals, or set differences. Intervals can be open, closed, half-open, finite, or infinite.

A function may come with its explicit domain, for example, for the function *f(x)=2x+3* where *0≤x<6,* its domain is the interval *[0,6),* because x can only be between those values. If the domain is not explicit and the function is given by an equation, the largest set of real numbers where the operations in the formula are possible will be considered as the domain. This is called the natural domain.

For the function *g(x)=1/x,* the operation is possible for all real numbers except zero, because if we set *x=0,* it leads to *1/0,* which is not a number. Thus, the natural domain of g is *D_g=R-\{0\}.* Writing it as a union of intervals, the domain is *D_g=(-∞,0)∪(0,+∞).*

The function *y=\sqrt{x}* takes a real number x and returns its square root. Since it's not possible to take the square root of a negative number in the field of real numbers, the domain of f is all non-negative real numbers, i.e., *x≥0* or the interval *[0, +∞).*

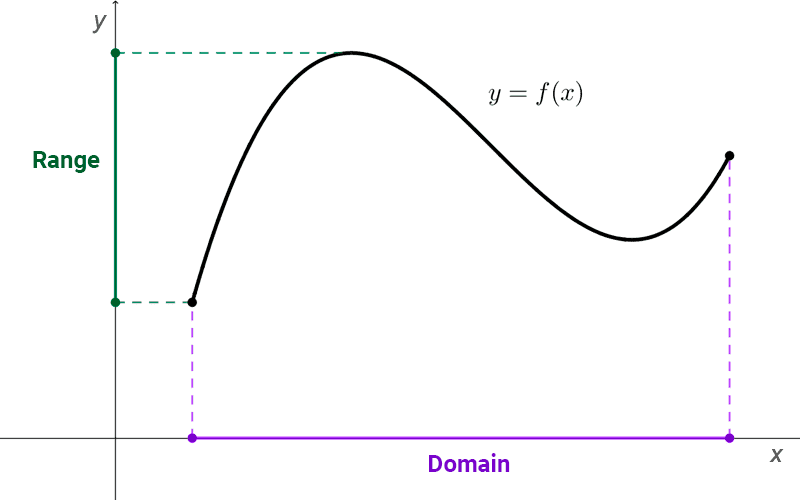
The domain of a function can be determined from its graph by projecting it onto the horizontal axis (x-axis). The interval it covers on this axis will be the domain.

The domain of a function can be restricted according to the context. For example, the area of a circle is given by the function *A=πr^2,* where *r* is the radius of the circle. Since we are only interested in positive values of *r* (because they are distances), the domain is restricted to *r>0,* or the interval *(0, +∞).*

We can also restrict domains as we see fit, as long as we indicate it properly. The domain of *y=x^2+7* is the entire set of real numbers. If we want to restrict it to, for example, only values of x greater than 4, we should write *y=x^2+7,* *x>4.*

Domains of function operations

If two functions f and g have domains *D_f* and *D_g* respectively, then the sum, difference, multiplication, and division of these functions have as their domain the set of values shared by the original domains. The domain of division excludes those values that make the denominator zero.

*D_{f+g}=D_f ∩ D_g*

*D_{f-g}=D_f ∩ D_g*

*D_{f\cdot g}=D_f ∩ D_g*

*D_{f/g}=D_f ∩ D_g - \{x~|~g(x)=0\}*

Domains of elementary functions

In general, to find the domain of a function, one must consider any restriction that may arise due to the mathematical operations defining the function. Some common restrictions include:

• Division by zero is not allowed.
• Square roots (or any even-index roots) of negative numbers are not defined in the set of real numbers.
• Logarithms of non-positive numbers cannot be calculated.

Polynomial functions

Polynomial functions are those of the form *f(x)=a_0+a_1x+a_2x^2+a_3x^3+…+a_nx^n* where *a_0,* *a_1,a_2,...,a_n* are real numbers called coefficients. The domain of every polynomial function is the set of real numbers, because there are no restrictions for the operations. That is, linear, quadratic, cubic, or any degree polynomial functions have the real numbers as their domain.

Examples

• The domain of the linear function *y=-3x+5* is *\mathbb{R}.*
• The domain of the quadratic function *f(x)=x^2+4x+5* is *\mathbb{R}.*
• The domain of the cubic function *y=-x^3+2x+4* is *\mathbb{R}.*

Rational functions

Rational functions are quotients of polynomial functions. The domain of every rational function is the set of real numbers excluding those that make the denominator zero.

Examples

• The domain of the function *f(x)=\dfrac{1}{x+1}* is *D_f=\{x~ |~ x+1\neq 0\}=\mathbb{R}-\{-1\}.* Expressed in interval notation, the domain is *D_f=(-∞,-1)∪(-1,+∞).*
• For the function *g(x)=\dfrac{x}{x^2-9},* since it must hold that *x^2-9\neq 0,* the domain is *D_g=\mathbb{R}-\{-3,3\}.* As an interval: *D_g=(-∞,-3)∪(-3,3)∪(3,+∞).*

Radical functions

Examples

• For *y=\sqrt{x+1},* the term *x+1* cannot be negative, meaning *x+1≥0,* which leads to *x≥-1.* The domain is then *[-1,+∞).*
• In the function *y=\sqrt{1-x^2},* the radicand *1-x^2* must be non-negative, that is, *1-x^2≥0,* resulting in *1≥x^2,* or *-1≤x≤1.* Thus, the domain is *[-1,1].*
• For *y=\sqrt[3]{x^2+\frac{2}{x}},* there are no restrictions with the radical since the index is odd, however, in the radicand x is in a denominator and cannot be zero, so the domain is *\mathbb{R}-\{0\}.*

Logarithmic functions

Logarithmic functions of any base have as their domain the set of real numbers that make their argument positive.

Examples

• For *y=\log(x),* the domain consists of all real numbers such that *x>0,* that is, the interval *(0,+∞).*
• In *y=\ln(x-7),* the argument *x-7* must be positive, meaning *x-7>0* which is equivalent to *x>7.* The domain is then *(7,+∞).*
• The function *y=\log_2(x^2-9)* cannot have a negative argument, so *x^2-9>0.* Solving for x yields *x<-3* or *x>3.* The domain is thus *(-∞,-3)∪(3,+∞).*

Exponential functions

The domain of exponential functions is the set of all real numbers, unless there is a restricted operation within the expression.

Examples

• The natural exponential function *y=e^x* has no operation restrictions, so its domain is all real numbers.
• In *y=e^{1/x},* since x is in the denominator, it cannot be zero. Except for that exception, all real numbers have an image. Therefore, the domain is *\mathbb{R}-\{0\}.*
• For the function *y=3^{\sqrt{x}},* the independent variable is inside a square root, so it must be non-negative. Therefore, the domain of the function is *[0,+∞).*

Trigonometric functions

The domains of trigonometric functions are expressed in the following table.

Function	Domain
Sine	*\mathbb{R}*
Cosine	*\mathbb{R}*
Tangent	*\mathbb{R}-\frac{n\pi}{2}* for odd integer n
Cosecant	*\mathbb{R}-n\pi* for any integer n
Secant	*\mathbb{R}-\frac{n\pi}{2}* for odd integer n
Cotangent	*\mathbb{R}-n\pi* for any integer n

Hyperbolic functions

The domains of hyperbolic functions are expressed in the following table.

Function	Domain
Hyperbolic sine	*\mathbb{R}*
Hyperbolic cosine	*\mathbb{R}*
Hyperbolic tangent	*\mathbb{R}*
Hyperbolic cosecant	*\mathbb{R}-\{0\}*
Hyperbolic secant	*\mathbb{R}*
Hyperbolic cotangent	*\mathbb{R}-\{0\}*

FAQs

Infographics