Inverse function
In this article we explain what is an inverse function going through its concept and definition, what are the necessary conditions for it to exist and the algebraic and geometric properties that it fulfills along with examples.
Table of Contents
What is an inverse function?
An inverse function is a function that undoes the effect of another function. In other words, if the original function transforms an element a into an element b, the inverse function transforms the element b back into the element a, returning it to its original state. The inverse of a function f(x) is symbolized as f-1(x), with the superscript "-1".
For example, if we consider the function *f(x)=2x,* this function takes a number *x* and multiplies it by two; its inverse function should take the result and return the number *x,* which is achieved by dividing by two. So, the inverse of *f* is *f^{-1}(x)=\frac{x}{2}.* In particular, if *x=2,* then *f(x)=4,* and if we input *4* into *f^{-1}(x),* we get *f^{-1}(4)=2,* which is the number we started with.
When does a function have an inverse?
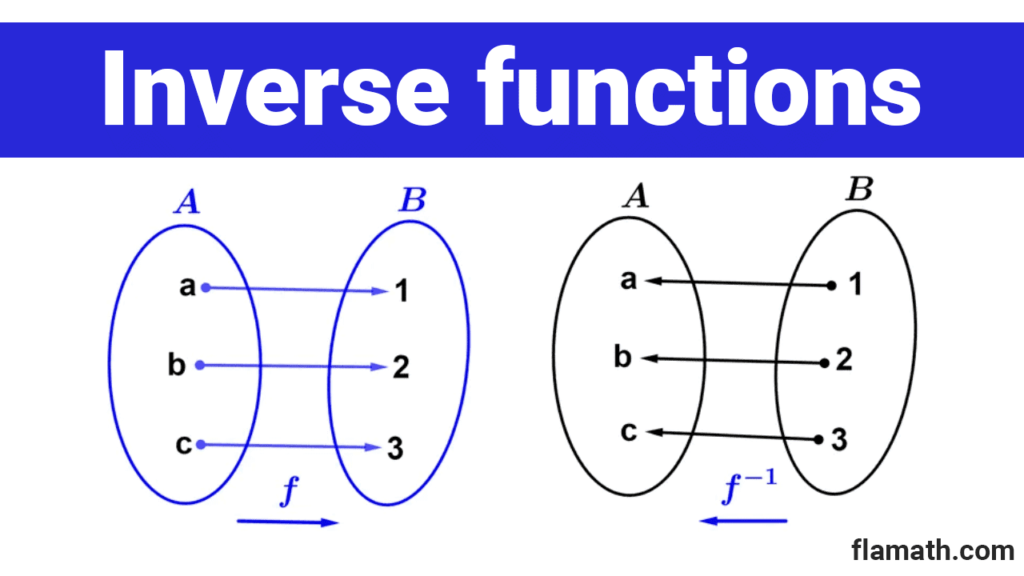
Not all functions have inverses. For a function to have an inverse, it must be bijective (one-to-one), which means that each element of the domain has exactly one corresponding element in the codomain, and that all elements of the codomain have at least one corresponding element in the domain.
Let's consider the quadratic function *f(x)=x^2.* This function takes the number x as input and returns its square. The task of an inverse would then be to take that square and return us the original number x. For example, for x=2, f(2)=4. The inverse should take that 4 and return us to 2. But there's a problem because also for x=-2, f(-2)=4. That is, both 2 and -2 map to the number 4.
There cannot be an inverse function in this case because it should return two different values if we input the number 4, not meeting the uniqueness condition of a function. So, the function *f(x)=x^2*, under these conditions, does not have an inverse because it is not bijective.
Now, if we consider another case, like the linear function *g(x)=2x+1,* things change. For example, for x=5, g(5)=11, and there is no other value in the domain that maps to the number 11. So, there exists an inverse function, which in this case will take 11 and return 5. This was possible because there are no different domain numbers that have the same image, in other words, the function is bijective.
Formal definition
Based on the previous reasoning, we can move from the concept to formally defining an inverse function, specifying the conditions that must be met for its existence.
Definition: Let f be a bijective function with domain A and range B. Then its inverse function f-1 has domain B and range A and is defined by:
*f^{-1}(y)=x~* if and only if *~f(x)=y~* for all *y* in B.
The definition says nothing different from what we have been doing. If f takes an x, transforms it, and returns a y, then the inverse f-1 takes that y, transforms it, and returns x; the same occurs in the reverse direction. The key is that f must be a bijective function. As we saw, this requirement is necessary so that, for each value of y, the value of f-1(y) is unique.

Important: *f^{-1}* is a symbol for the inverse function of *f.* The *-1* used is not an exponent. That is, *f^{-1}* does not mean *\frac{1}{f(x)}.*
An important characteristic is that the domain of the original function is the range of the inverse, and the range of the inverse function is equal to the domain of the original function. Thus:
Domain of f = Range of f-1
Range of f = Domain of f-1
By performing a small replacement work, we can arrive at the following expressions, known as cancellation equations. If *f* and *f^{-1}* are inverse functions, it is verified that:
*f^{-1}(f(x))=x~* for all x in the domain of f
*f(f^{-1}(x))=x~* for all x in the range of f
In other words, the composition of a function with its inverse, or of an inverse with the original, results in the identity function. We can use these equations to verify that two functions are inverses. For example, we will prove that *f(x)=2x* has *f^{-1}(x)=\frac{x}{2}:*
*f^{-1}(f(x))=f^{-1}(2x)=\dfrac{2x}{2}=x*
*f(f^{-1}(x))=f \left(\dfrac{x}{2} \right)=2 \left(\dfrac{x}{2} \right)=x*
There is a theorem that ensures that if a function is increasing or decreasing on an interval, then it is bijective and has an inverse on that interval. In fact, if *f* is increasing on the interval I, it satisfies the inequality *f(x_2)>f(x_1)* when *x_2>x_1,* which ensures that there will be no equal images; then, f is bijective and has an inverse. The same occurs with decreasing functions.
Functions that are neither increasing nor decreasing may still be bijective and have an inverse, such as the function *f(x)=\frac{1}{x}* for *x≠0* and *f(0)=0,* defined in *\mathbb{R}.*
Graphs of inverse functions
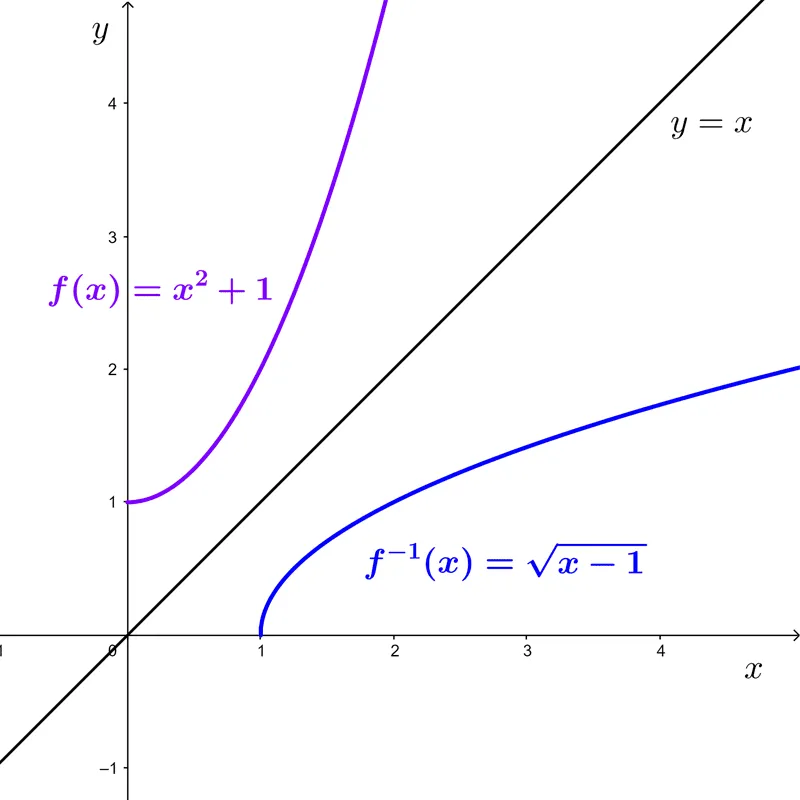
The function graph and its inverse are symmetrical with respect to the line y=x. Thus, one can be obtained from the other by reflection.
This is because, as *f(a)=b* if and only if *f^{-1}(b)=a,* the point *(a,b)* is on the graph of *f* if and only if the point *(b,a)* is on the graph of *f^{-1}.* However, we obtain the point *(b,a)* from *(a,b)* by reflecting with respect to the line with equation *y=x.* Also, the points of intersection of a function with the x and y axes are the same as those of its inverse function, but swapped.
Properties
Below are the characteristics of inverse functions.
- A function has an inverse only if it is bijective, and this inverse is another bijective function.
- If a function is increasing or decreasing on an interval, then it has an inverse on that interval.
- The domain of a function is the range of its inverse, and the range of the inverse is equal to the domain of the original function.
- The graphs of two inverse functions are symmetrical with respect to the line y=x.
- The points of intersection of a function with the x and y axes are the same as those of its inverse function, but swapped.
- The composition of a function with its inverse, or of an inverse with the original, results in the identity function.
- The inverse function of an inverse function is equal to the original function. In symbols: *(f^{-1})^{-1}=f*
Examples
Having verified that a function is bijective, to calculate its inverse, we must follow these steps:
- Write y=f(x).
- Solve for x in terms of y in this equation (if possible).
- Express f-1 as a function of x by swapping x and y. The resulting equation is y=f-1(x).
Next, we'll see some examples of known functions and their inverses. The aforementioned steps can be followed to confirm the results.
Linear Functions
All non-constant linear functions are bijective and have inverses. A function *f(x)=ax+b* where *a* and *b* are real numbers and *a\neq 0* has an inverse function
*f^{-1}(x)=\dfrac{x-b}{a}*
Constant functions of the form *f(x)=b* do not have inverses because they are not bijective.
Example: the inverse of the linear function *f(x)=-3x-4* is *f^{-1}(x)=-\dfrac{x+4}{3}*
Quadratic Functions
As we saw earlier, the quadratic function *y=x^2* is not bijective, therefore, it does not have an inverse. However, if we consider a subset of its domain where this condition is met, we can find an inverse. This same principle applies to all quadratic functions.
Example: given the function *f(x)=x^2+1,* if we take the non-negative real numbers as the domain *(x≥0),* the inverse exists and is *f^{-1}(x)=\sqrt{x-1}.* Thus, the inverse of this quadratic function is a square root function.
Note: If instead of restricting the domain to non-negative numbers, we decide to restrict it to non-positive numbers *(x≤0),* to maintain congruence, in the solving of the inverse, we must take the negative square root, so that the domain of the original function matches the range of the inverse. Thus, for *f(x)=x^2+1,* where *x≤0,* the inverse function is *f^{-1}(x)=-\sqrt{x-1}*
Cubic functions
Cubic functions without quadratic or linear terms are bijective, hence we can find an inverse. Introducing such terms may cause bijectivity to be lost.
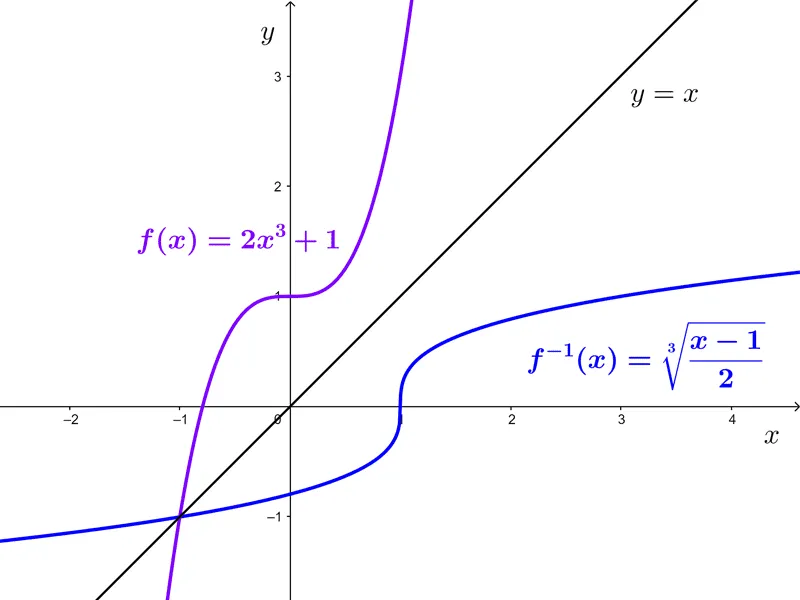
Example: *f(x)=2x^3+1* has an inverse *f^{-1}(x)=\sqrt[3]{\dfrac{x-1}{2}},* meaning the inverse of a cubic function involves a cube root function.
Radical functions
Radical functions are those in which the independent variable appears within a square root, cube root, or other index. It is necessary to verify in each case bijectivity and if the solving for the inverse is possible.
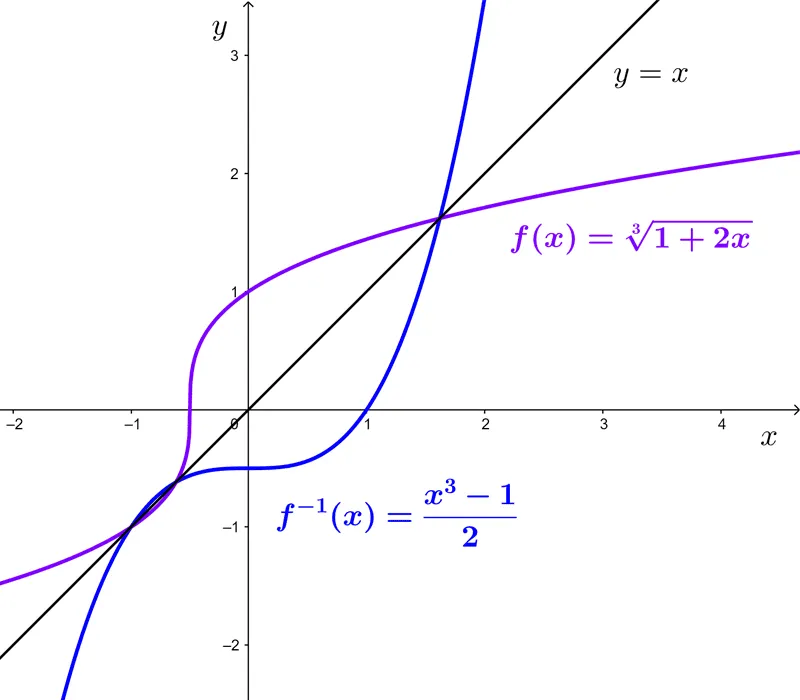
Example 1: the function *f(x)=\sqrt[3]{1+2x}* is bijective and its inverse is *f^{-1}(x)=\dfrac{x^3-1}{2}*
Example 2: the function *g(x)=\sqrt{x-3}* is bijective and its inverse is *g^{-1}(x)=x^2+3.* It is important to note that the range of *g* is *[0,+∞),* whereas the domain of *g^{-1},* if not specified, is *\mathbb{R}.* To avoid this incongruity and ensure that the property that comes with the definition is fulfilled, we must restrict the domain of *g^{-1}* to *[0,+∞)*.
Finally, the inverse of *g* is *g^{-1}(x)=x^2+3* with *D_{g^{-1}}=[0,+∞)*
Rational functions
In rational functions, it will be necessary to first verify bijectivity. There are some in which this condition is met.
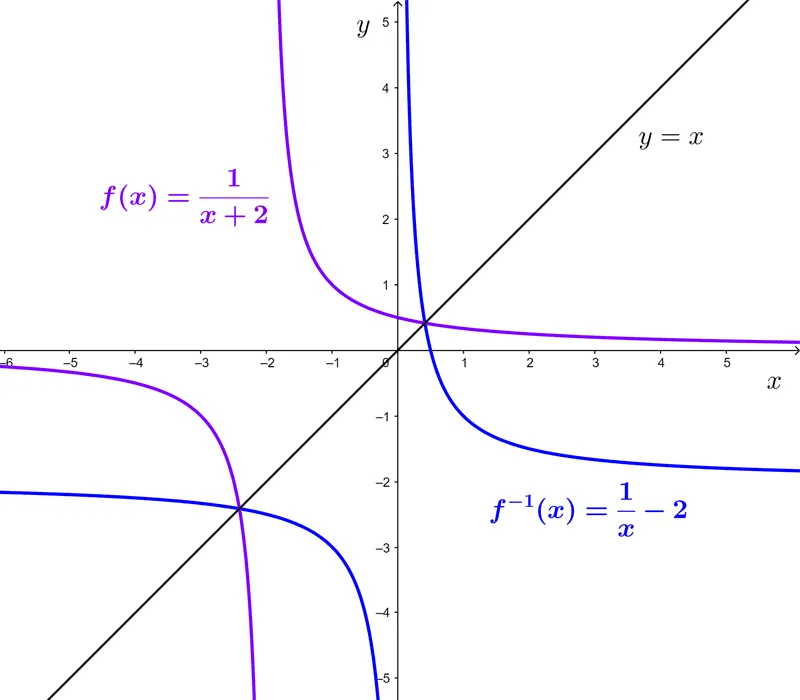
Example: The rational function *f(x)=\dfrac{1}{x+2}* is bijective and its inverse is *f^{-1}(x)=\dfrac{1}{x}-2.*
Exponential and logarithmic functions
Exponential and logarithmic functions are closely related and are inverses of each other. An exponential function *f(x)=a^x* where *a* is positive and not equal to 1 has an inverse logarithmic function *f^{-1}(x)=\log_a{x}.* Some particular cases are:
- The natural exponential function *f(x)=e^x* is the inverse of the natural logarithm function *f^{-1}(x)=\ln{x}.*
- The decimal exponential function (base 10) *f(x)=10^x* is the inverse of the decimal logarithm function *f^{-1}(x)=\log{x}.*
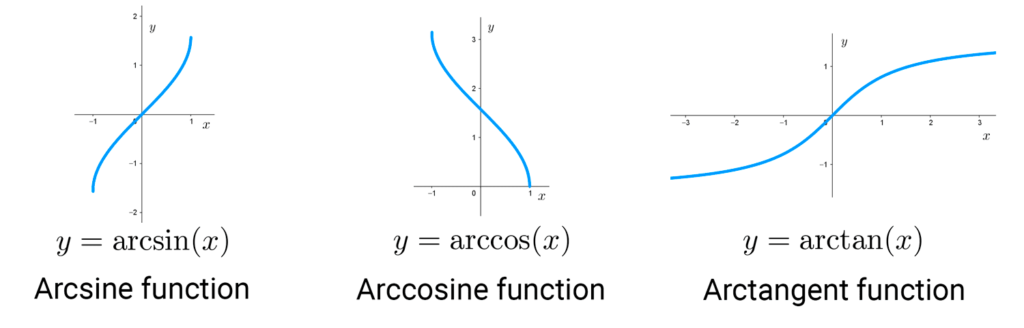
Trigonometric functions
Trigonometric functions are not bijective in their natural domains; however, we can apply convenient restrictions so that these functions have an inverse. Thus, the sine, cosine, and tangent functions have as inverses the arcsine, arccosine, and arctangent functions, respectively.
The following table shows each function with its inverse, along with the domain and range of the inverse function.
| Trigonometric function | Inverse function | Domain of inverse | Range of inverse |
|---|---|---|---|
| *\sin(x)* | *\arcsin(x)* | *[-1, 1]* | *[-\frac{π}{2}; \frac{π}{2}]* |
| *\cos(x)* | *\arccos(x)* | *[-1, 1]* | *[0, π]* |
| *\tan(x)* | *\arctan(x)* | *(-∞, +∞)* | *(-\frac{π}{2}; \frac{π}{2})* |
FAQs
Do all functions have inverses?
No, not all functions have an inverse. For a function to have an inverse the necessary condition is that it is bijective, which means that each element of the domain maps to exactly one element of the codomain and vice versa.
What is the relationship between the domain and range of a function and its inverse?
The domain and range of a function and its inverse are interchanged. Thus, the domain of the original function is the range of its inverse, and the range of the original is the domain of the inverse.
How do you know if two functions are inverses of each other?
Two functions are inverses of each other if the composition of one with the other results in the identity. That is, applying the original function to an element and then applying the inverse to the result should result in the element with which it started.
What do the graphs of two inverse functions look like?
The graphs of two inverse functions are symmetric with respect to the identity line y=x. This means that if you reflect the graph of a function on the line y=x, you will obtain the graph of its inverse function. This is a direct consequence of the definition of an inverse function.
Can a function have more than one inverse function?
No, a function cannot have more than one inverse function. If a function has an inverse, that inverse is unique.
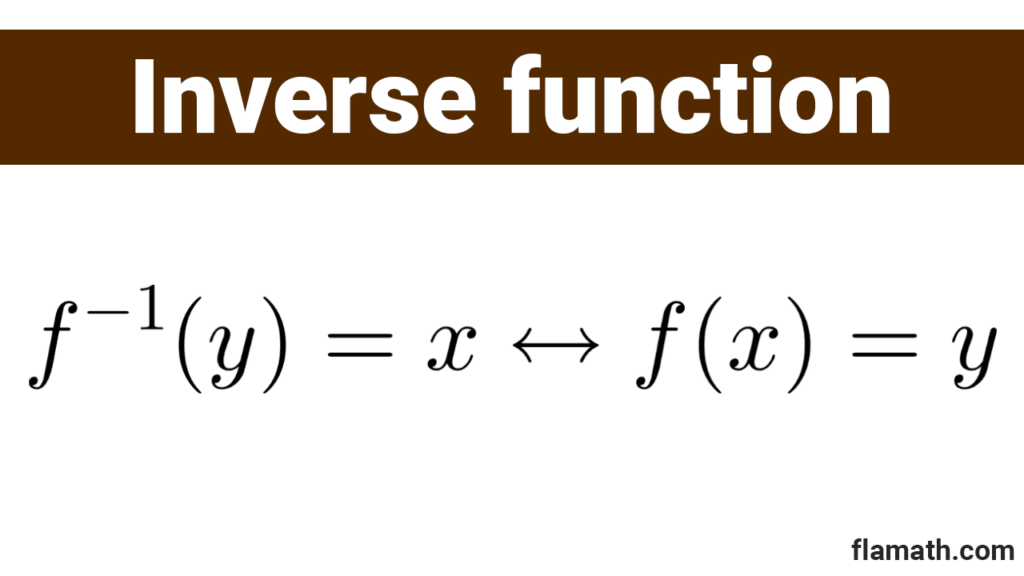



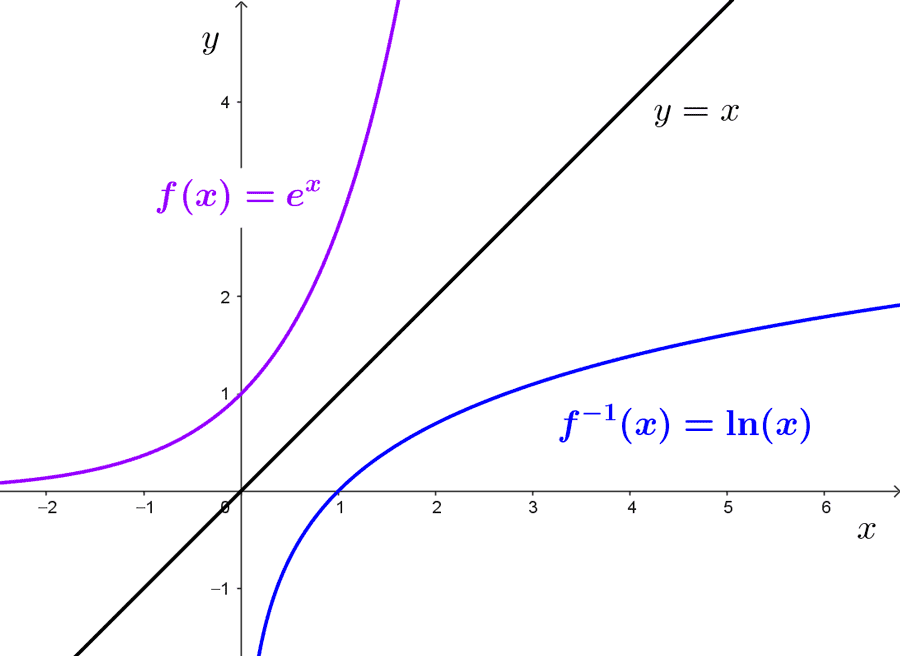



Other articles that may interest you