
Fundamental trigonometric limit
In this article we study the fundamental trigonometric limit with a demonstration of it and examples of application for the calculation of limits.
Table of Contents
Limits involving sine function
The following is known as the important limit or fundamental limit:
$$\lim_{x\to 0} \dfrac{\sin x}{x}=1$$
As the independent variable is an angle, it is common to use the symbol *\theta* to represent it. Therefore, an equivalent expression of the fundamental trigonometric limit is:
$$\lim_{\theta \to 0} \dfrac{\sin \theta}{\theta}=1$$
We will use this symbolism for the proof.
Note: When dealing with functions, angles are measured in radians (circular system) because this way they are real numbers. It is not common to use other systems like sexagesimal degrees.
Demonstration of the fundamental limit
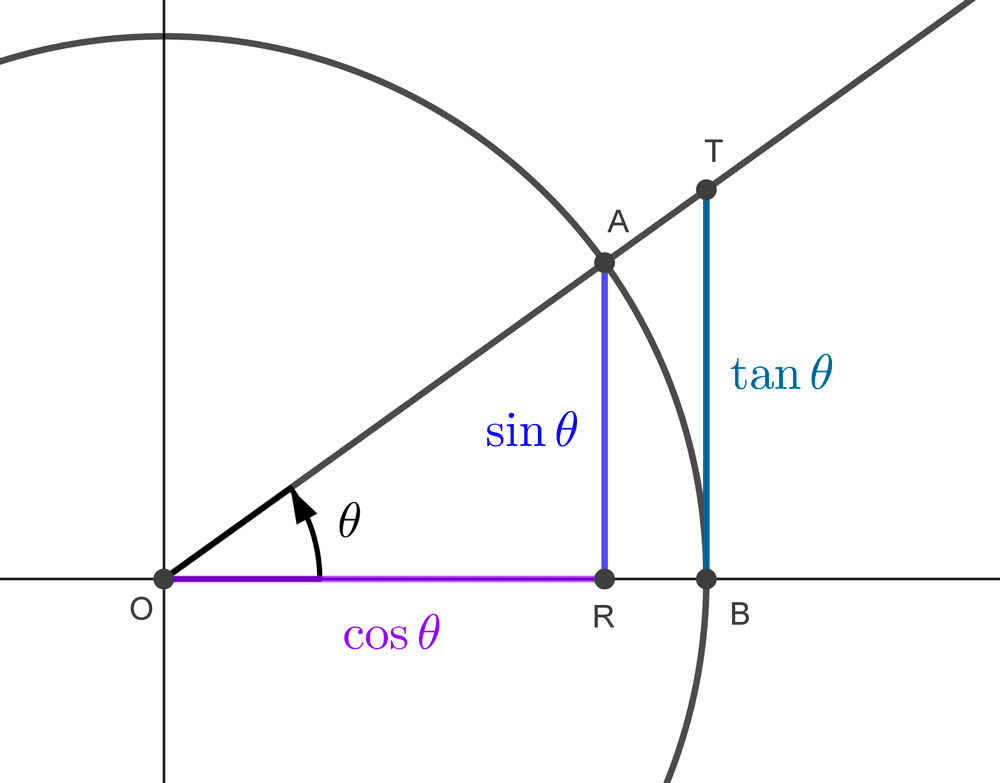
In a circle of radius 1, we consider the central angle *\theta.* The measure of the arc AB determined on the circumference is *\theta.* At B, the tangent TB is drawn. In this way, three figures are formed: two triangles and a circular sector that satisfy the following relationship:
Area AOR < sector AOB < Area TOB
The corresponding areas can be expressed in terms of *\theta:*
Area of triangle AOR *=\dfrac{1}{2}~ \text{base} \cdot \text{height}=\dfrac{1}{2} \cos \theta \cdot \sin \theta*
Area of circular sector AOB *=\dfrac{1}{2}r^2\cdot \theta=\dfrac{1}{2}(1)^2\cdot \theta=\dfrac{1}{2}~\theta*
Area of triangle TOB *=\dfrac{1}{2}~ \text{base} \cdot \text{height}=\dfrac{1}{2} 1 \cdot \tan \theta=\dfrac{1}{2} \tan \theta*
In the following diagram, each figure can be clearly seen:
Replacing the obtained data in the initial inequality, we get:
*\dfrac{1}{2} \cos \theta \cdot \sin \theta < \dfrac{1}{2}~\theta< \dfrac{1}{2}\tan \theta*
Dividing by *\dfrac{1}{2} \sin \theta* (which is a positive factor if *\theta* is positive),
*\cos \theta < \dfrac{\theta}{\sin \theta}<\dfrac{1}{\cos \theta}*
Taking the reciprocals, the inequalities are reversed
*\dfrac{1}{\cos \theta} > \dfrac{\sin \theta}{\theta} > \cos \theta*
This inequality also holds if we change *\theta* to *-\theta,* since in that case:
*\dfrac{1}{\cos (-\theta)}=\dfrac{1}{\cos \theta}~* and *~\cos (-\theta)=\cos \theta* (because the cosine is an even function).
*\dfrac{\sin (-\theta)}{(-\theta)}=\dfrac{-\sin \theta}{(-\theta)}=\dfrac{\sin \theta}{\theta}* (because sine and *\theta* are odd functions).
If we make *\theta* tend to *0,* *\cos \theta \to 1.* Therefore, it must be:
$$\lim_{\theta \to 0} \dfrac{\sin \theta}{\theta}=1$$
This result can be expressed by saying that, at the origin, *\sin \theta* is an infinitesimal equivalent to *\theta.*

As mentioned earlier, the function *f(x)=\dfrac{\sin x}{x}* is even, which means it is symmetric about the y-axis. As the values of *\sin x* are between +1 and -1, the values of *f(x)* are between *y_1=\dfrac{1}{x}* and *y_2=-\dfrac{1}{x}*
Trigonometric identities useful for calculating limits
The following identities can be useful when determining the value of limits.
Tangent is equal to sine over cosine: *\tan(x) = \dfrac{\sin(x)}{\cos(x)}*
Pythagorean identities:
*\sin^2(x) + \cos^2(x) = 1*
*1 + \tan^2(x) = \sec^2(x)*
*1 + \cot^2(x) = \csc^2(x)*
Reciprocal identities:
Cosecant: *\csc(x) = \dfrac{1}{\sin(x)}*
Secant: *\sec(x) = \dfrac{1}{\cos(x)}*
Cotangent: *\cot(x) = \dfrac{1}{\tan(x)}*
Double angle identities:
*\sin(2x)=2\sin(x)\cos(x)*
*\cos(2x)=\cos^2(x) - \sin^2(x)*
*\tan(2x)=\dfrac{2\tan(x)}{1-\tan^2(x)}*
Sum and difference identities:
*\sin(a \pm b) = \sin(a)\cos(b) \pm \cos(a)\sin(b)*
*\cos(a \pm b) = \cos(a)\cos(b) \mp \sin(a)\sin(b)*
*\tan(a \pm b) = \dfrac{\tan(a) \pm \tan(b)}{1 \mp \tan(a)\tan(b)}*
Examples of application of the fundamental trigonometric limit
We will see below some examples of limits that can be calculated using the important trigonometric limit.
Direct application
In these problems, it is sufficient to rearrange the expressions using algebraic properties and limits properties to be able to apply the fundamental limit.
Example 1: Find the value of the limit *\lim_{x\to 0} \dfrac{\sin x}{5x}*
Solution: Direct substitution leads to the indeterminate form 0/0. However, we can use an algebraic property to rewrite the expression and then use a limit property to move the constant outside the limit. Thus:
*\lim_{x\to 0} \dfrac{\sin x}{5x}=\lim_{x\to 0} \left(\dfrac{1}{5}\cdot\dfrac{\sin x}{x}\right)*
*=\dfrac{1}{5} \lim_{x\to 0}\dfrac{\sin x}{x}*
*=\dfrac{1}{5} (1)*
*=\dfrac{1}{5}*
Example 2: Calculate the limit *\lim_{x\to 0} \dfrac{\tan x}{x}*
Solution: Direct substitution leads to the indeterminate form 0/0. To solve this problem, we use the trigonometric identity *\tan x=\dfrac{\sin x}{\cos x}*. Rearranging the expression, we get:
*\lim_{x\to 0} \dfrac{\tan x}{x}=\lim_{x\to 0} \left(\tan x\cdot \dfrac{1}{x}\right)*
*=\lim_{x\to 0} \left(\dfrac{\sin x}{\cos x}\cdot \dfrac{1}{x}\right)*
*=\lim_{x\to 0} \left(\dfrac{\sin x}{x}\cdot \dfrac{1}{\cos x}\right)*
*=\left(\lim_{x\to 0} \dfrac{\sin x}{x}\right) \left(\lim_{x\to 0}\dfrac{1}{\cos x}\right)*
*=(1)(1)*
*=1*
Application by substitution
In this type of problems, it is not enough to rearrange the expressions; it will also be necessary to apply a variable change to use the fundamental limit.
Example 3: Calculate the following limit: *\lim_{x\to 0} \dfrac{\sin 2x}{5x}*
Solution: We cannot apply the fundamental limit directly because for that, the denominator of the quotient should be 2x. However, we can obtain it by multiplying the numerator and denominator by 2/5:
*\lim_{x\to 0} \dfrac{\sin 2x}{5x}=\lim_{x\to 0} \dfrac{(2/5)\cdot \sin 2x}{(2/5)\cdot 5x}*
*=\dfrac{2}{5}\cdot \lim_{x\to 0} \dfrac{\sin 2x}{2x}*
Now we can use the important limit, considering *\theta=2x.* Then:
*\lim_{x\to 0} \dfrac{\sin 2x}{5x}=\dfrac{2}{5}\cdot \lim_{\theta \to 0} \dfrac{\sin \theta}{\theta}*
*=\dfrac{2}{5}\cdot 1*
*=\dfrac{2}{5}*
Example 4: Determine the value of the following limit *\lim_{x\to 0} \dfrac{\tan3x}{x}*
Solution: Similarly to the previous example, we rewrite the expression to be able to use the fundamental limit:
*\lim_{x\to 0} \dfrac{\tan3x}{x}=3\left(\lim_{x\to 0} \dfrac{\tan3x}{3x}\right)*
If we let *\theta=3x,* then when *x\to 0, \theta\to 0:*
*3\left(\lim_{x\to 0} \dfrac{\tan3x}{3x}\right)=3\left(\lim_{\theta \to 0} \dfrac{\tan\theta}{\theta}\right)*
*=3\left(\lim_{\theta \to 0} \dfrac{\sin\theta}{\theta \cos\theta}\right)* (because *\tan\theta=\sin\theta/\cos\theta*)
*=3\left(\lim_{\theta \to 0} \dfrac{\sin\theta}{\theta}\right)\left(\lim_{\theta \to 0} \dfrac{1}{\cos\theta}\right)*
*=3\cdot 1\cdot \dfrac{1}{1}*
*=3*
Limits involving cosine and tangent
Starting from the limit *\lim_{x\to 0} \dfrac{\sin x}{x}=1*, the following limits can be demonstrated:
$$\lim_{x\to 0} \dfrac{\cos x-1}{x}=0$$
$$\lim_{x\to 0} \dfrac{\tan x}{x}=1$$
Demonstrations
1) *\lim_{x\to 0} \dfrac{\cos x-1}{x}=0 *
Multiplying and dividing by the conjugate of the numerator:
*\lim_{x\to 0} \dfrac{\cos x-1}{x}=\lim_{x\to 0}\left(\dfrac{\cos x-1}{x}\cdot \dfrac{\cos x+1}{\cos x+1}\right)*
*=\lim_{x\to 0}\dfrac{\cos^2x-1}{x(\cos x+1)}*
*=\lim_{x\to 0}\dfrac{-\sin^2x}{x(\cos x+1)}*
*=-\lim_{x\to 0}\left(\dfrac{\sin x}{x}\cdot \dfrac{\sin x}{\cos x+1}\right)*
*=-1\cdot \dfrac{0}{1+1}*
*=0*
So: *\lim_{x\to 0} \dfrac{\cos x-1}{x}=0*
2) *\lim_{x\to 0} \dfrac{\tan x}{x}=1*
*\lim_{x\to 0} \dfrac{\tan x}{x}=\lim_{x\to 0} \left(\tan x\cdot \dfrac{1}{x}\right)*
*=\lim_{x\to 0} \left(\dfrac{\sin x}{\cos x}\cdot \dfrac{1}{x}\right)*
*=\lim_{x\to 0} \left(\dfrac{\sin x}{x}\cdot \dfrac{1}{\cos x}\right)*
*=\left(\lim_{x\to 0} \dfrac{\sin x}{x}\right) \left(\lim_{x\to 0}\dfrac{1}{\cos x}\right)*
*=(1)(1)*
*=1*
So: *\lim_{x\to 0} \dfrac{\tan x}{x}=1*

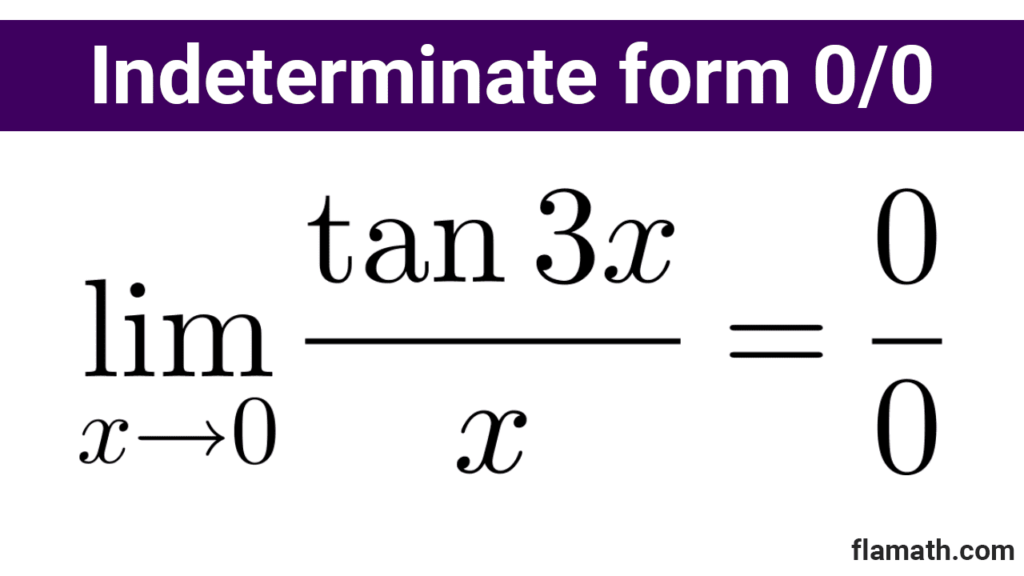
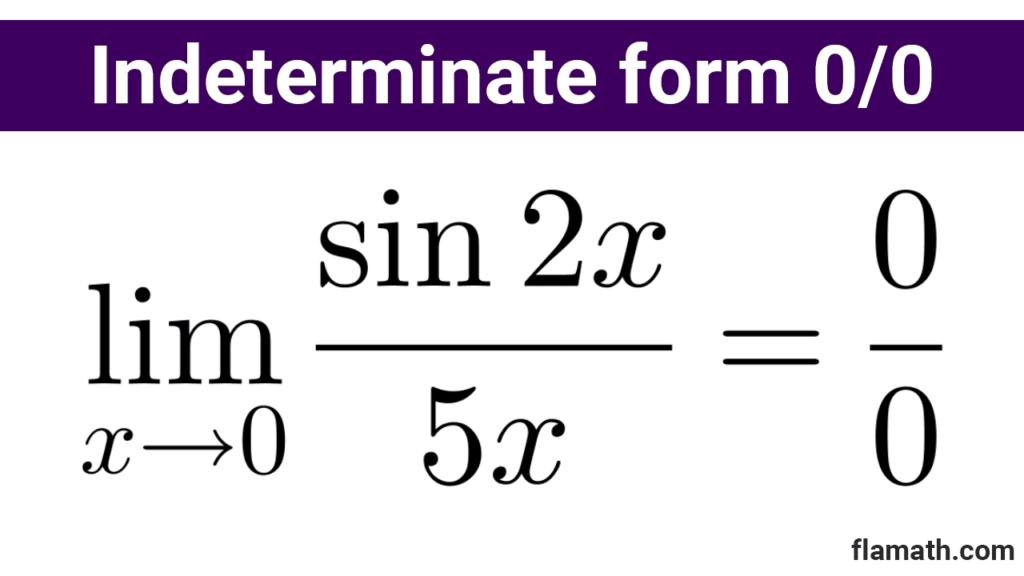



Other articles that may interest you