Limits of constant functions

In this article, we explore the limits of a constant function at a point, positive infinity, and negative infinity. Additionally, we'll go through some examples for better understanding.

Recall that a constant function is a real function of the form *f(x)=k* where k is any real number. Its domain is the set of real numbers, and its range is the set {k}, meaning *D_f=\mathbb{R}* and *R_f=\{k\}.*

Table of Contents

Limit at a point

The limit of a constant function at a point is equal to the value of the function at that point, i.e., the same constant.

Let *f(x)=k* be a function defined on *\mathbb{R}* and *k* be a real number, then:

$$\lim_{x\to a} f(x)=\lim_{x\to a} k=k$$

Graphical representation of the limit of a constant function — In the graph, it can be observed that as we approach the point *a*, the function's values get closer to the value *k*

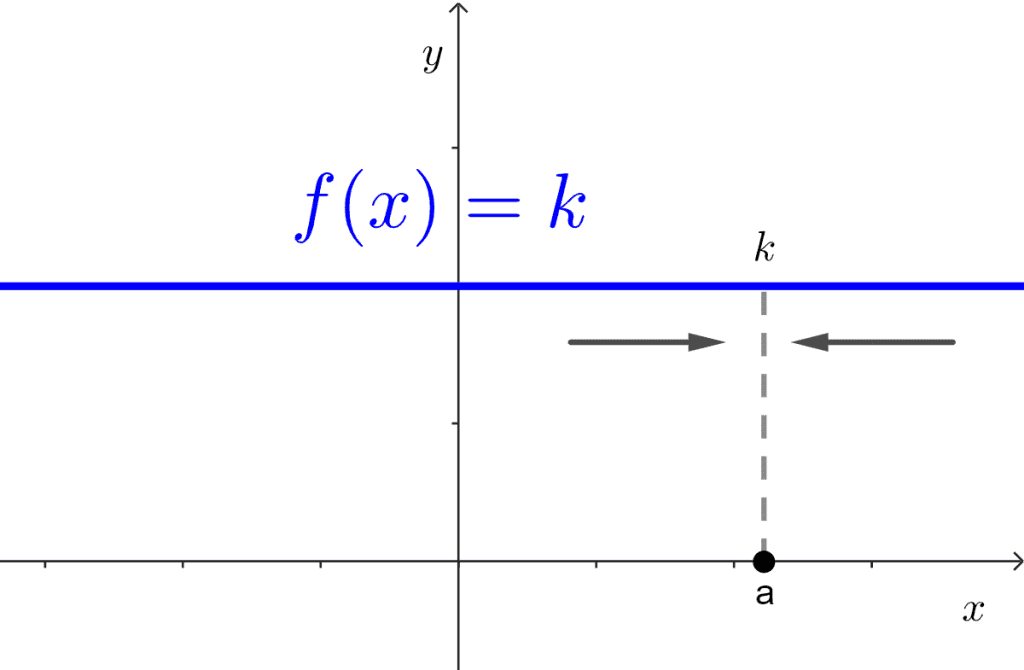
Proof:

To prove that the number *k* is the sought limit, we need to find, for any positive number epsilon, a positive number delta that satisfies the condition required by the definition.

In this case, delta can be any positive number, because for any epsilon and any positive delta, it turns out that:

If *0<|x-a|<\delta,* then *|k-k|=0<\epsilon*

That is, the definition of limit is satisfied for *f(x)=k* and *L=k*

Examples:

If *f(x)=5,* then *\lim_{x\to 9} f(x)=\lim_{x\to 9} 5=5*

*\lim_{x\to 3} -20=-20*

*\lim_{x\to -1} \sqrt{2}=\sqrt{2}*

*\lim_{x\to -\frac{2}{3}} -3=-3*