Limits of Identity Function

In this article, we explore the limits of the identity function both at a point and as the variable approaches positive and negative infinity, accompanied by examples for better comprehension.

Remember that the identity function is a real function of the form *f(x)=x.* Its domain and range are the set of real numbers, that is, *D_f=\mathbb{R}* and *R_f=\mathbb{R}.*

Table of Contents

Limits at a point

The limit of the identity function at a point is equal to the value at that point.

Let the identity function be *f(x)=x* where *D_f=\mathbb{R}*, then:

$$\lim_{x\to a} f(x)=\lim_{x\to a} x=a$$

Limit of the identity function at a point — In the graph, it can be observed that as we approach the point 'a,' the function's images approach the value f(a)=a

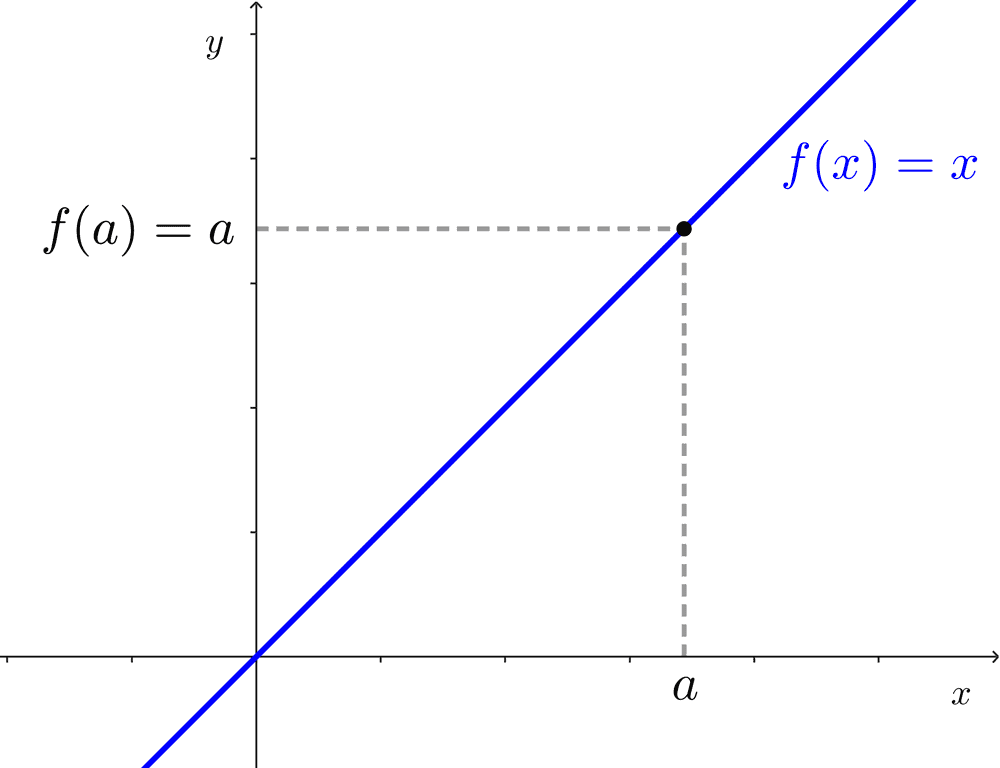
Examples:

*\lim_{x\to 4} x=4*

*\lim_{x\to -2} x=-2*

*\lim_{x\to \sqrt{2}} x=\sqrt{2}*

*\lim_{x\to 0} x=0*

Proof:

To prove that *\lim_{x\to a} x=a*, for each positive *\epsilon*, we must find a positive *\delta* such that for every *x*, it holds that:

if *0<|x-a|<\delta* then *|x-a|<\epsilon*

The implication will hold if *\delta* is equal to *\epsilon* or any positive number less than that. Therefore, *\lim_{x\to a} x=a*

Limits at infinity

The limit of the identity function as the variable tends to positive infinity or negative infinity is equal to positive infinity and negative infinity, respectively:

$$\lim_{x\to \infty} x=\infty$$

$$\lim_{x\to -\infty} x=-\infty$$

Examples of limits of the identity function at a point and at infinity

Daniel Machado

Advanced student of Mathematics at Facultad de Ciencias Exactas, Químicas y Naturales. Universidad Nacional de Misiones, Argentina.