
Function operations
In this article, we develop operations between functions, both algebraic operations such as addition, subtraction, multiplication, and division, and also function composition.
Table of Contents
Sum of functions
Let *f* and *g* be two functions with domains *D_f* and *D_g*, respectively.
Sum function of f and g is the function *(f+g)(x)=f(x)+g(x)*
Since f and g must be defined, the domain of the sum of functions is the set of values shared by their domains: $$D_{f+g}=D_f \cap D_g$$
Example: *f(x)=x+2* and *g(x)= \sqrt{x}*
The corresponding domains are:
*D_f=\mathbb{R}*
*D_g=[0,+∞)*
*(f+g)(x)=f(x)+g(x)=x+2+\sqrt{x}*
*D_{f+g}=D_f \cap D_g =[0,+∞)*
Subtraction of functions
Subtraction function of f and g is the function *(f-g)(x)=f(x)-g(x)*
The domain of the subtraction of functions is also the set of values shared by their domains: $$D_{f-g}=D_f \cap D_g$$
Example: *f(x)=x^2+1* and *g(x)=\ln(x+1)* (*\ln* is the natural logarithm)
The corresponding domains are:
*D_f=\mathbb{R}*
*D_{g} =\{x∈\mathbb{R}/x+1>0\}=( -1,+∞)*
*(f-g)(x)=f(x)-g(x)=x^2+1-\ln(x+1)*
*D_{f-g}=D_f \cap D_g=(-1,+∞)*
Product of functions
Product function or multiplication of f and g is the function *(fg)(x)=f(x)\cdot g(x)*
The domain of the product of functions is the set of values shared by their domains: $$D_{fg}=D_f \cap D_g$$
Example: *f(x)=\sqrt{x}* and *g(x)=\sqrt{2-x}*
The corresponding domains are:
*D_f=[0, ∞)*
*D_g=\{x∈\mathbb{R}/2-x≥0\}=(-∞, 2]*
*(fg)(x)=f(x) \ g(x)=\sqrt{x} \ \sqrt{2-x}*
*D_{fg}=D_f \cap D_g=[0,2]*
Quotient of functions
Quotient function or division of f and g is the function *\left(\dfrac{f}{g}\right)(x)=\dfrac{f(x)}{g(x)}*
The domain of the quotient of functions is the set of values shared by their domains, excluding those where *g(x)* is equal to zero: $$D_{f/g}=D_f \cap D_g-\{x∈\mathbb{R}~|~g(x)=0\}$$
Example: *f(x)=x^2+6* and *g(x)=x-2*
The corresponding domains are:
*D_f=\mathbb{R}*
*D_g=\mathbb{R}*
*\left(\dfrac{f}{g}\right)(x)=\dfrac{f(x)}{g(x)}= \dfrac{x^2 +6}{x-2}*
*D_{f/g}=D_f \cap D_g-\{x∈\mathbb{R}~|~x-2=0\}=\mathbb{R}-\{2\}*
Composition of functions
Composition of functions f and g is the function *(f \circ g)(x)=f(g(x))* (read as "f circle g," "g composed with f," or "f of g")
The domain of the composition of functions is the set of all values in the domain of g for which g(x) is in the domain of f: $$D_{f \circ g}=\{x∈\mathbb{R}~|~x∈D_g∧g(x)∈D_f\}$$
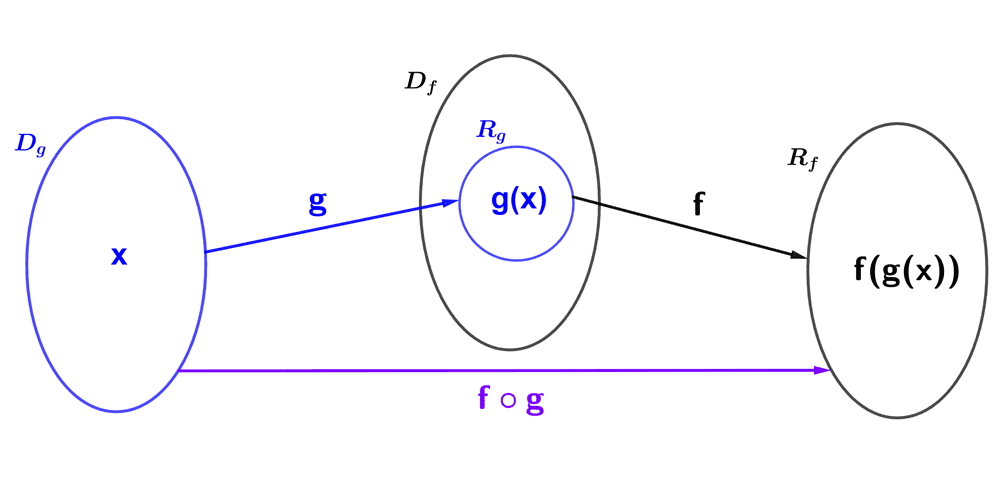
The function g has the domain Dg and range Rg, while the function f has the domain Df and range Rf. We are interested in the images of g that are within the domain of f because only they can be passed through f. For this reason, we only consider the elements of the domain of g that return an image contained in the domain of f. If there are no such elements, then we cannot compose the functions.
It is necessary for composition to be possible that the range of g is included in the domain of f, i.e., *R_{g}⊆D_{f}*. This is called the composition condition.
The function *f \circ g* acts as a "bridge" from a subset of *D_g* to the set *R_f*. That subset of *D_g* is precisely the domain of the composite function. You can see this in the following diagram:
Example: *f(u)=\sqrt{u}* and *g(x)=2-x*
Before anything else, we must ensure that the composition condition is met, i.e., *R_{g}⊆D_{f}*. We find both sets and see that it is indeed satisfied because:
*R_g=[0, +∞)* and *D_f=\mathbb{R}*, so it happens that *R_g⊆D_f*.
To find *f \circ g*, we first apply *g* to *x* and then apply *f* to *g(x)*.
*(f \circ g)(x)=f(g(x))*
*(f \circ g)(x)=f(2-x)*
*(f \circ g)(x)=\sqrt{2-x}*
The domain of *f \circ g* can be obtained from the last expression because we know that a square root must have a non-negative radicand (as the square root of a negative number is not a real number). So:
*D_{f \circ g}=\{x/2-x≥0\}=\{x/x≤2\}=(-\infty, 2]*
Note that in this case, *D_{f \circ g}* is not equal to *D_g*.
FAQs
What are the operations on functions?
The basic operations between functions are addition, subtraction, multiplication and division. These operations are performed in a similar way as with numbers, but applied to functions.
How to add and subtract functions?
Addition or subtraction of functions is performed by adding or subtracting the corresponding values of the functions. The domain is the intersection of the original domains.
How to multiply functions?
Multiplication of two functions is done by multiplying the corresponding values of the functions. The domain of the new function is the intersection of the domains of the original functions.
How to divide functions?
The division of two functions is performed by dividing the corresponding values of the functions. It is important to note that the denominator function must not be equal to zero to avoid undefined divisions. The domain of the new function is the intersection of the domains of the original functions excluding those values that cancel the denominator.




Other articles that may interest you