
Multiplication of functions
In this article we explain how to multiply real functions with step-by-step exercises. In addition, we will see the properties of this operation.
Table of Contents
How to multiply functions?
The multiplication of two functions is defined as the product of the function images. That is, to obtain the product, you must multiply the two function equations.
*(f\cdot g)(x)=f(x)\cdot g(x)*
The domain of the product function is the intersection of the domains of f and g, i.e., the numbers that are in both domains:
*D_{fg}=D_f\cap D_g*
When functions are multiplied, many of the properties of the original functions can be preserved, but this depends on the specific properties you are considering. In particular, the product of two even functions or two odd functions results in an even function. Conversely, if an even function and an odd function are multiplied, the result is odd.
Solved exercises
Example 1
Given the functions *f(x)=3x-4~* and *~g(x)=-6x-1,* find *(fg)(x)* and its domain.
Solution: functions f and g are polynomials, thus their domain is the set of real numbers, *\mathbb{R}.* The intersection of their domains is the same set, so the domain of the product function is *D_{fg}=\mathbb{R}.*
To obtain the analytical expression, we multiply the two equations.
*(fg)(x)=f(x)\cdot g(x)*
*=(3x-4)(-6x-1)*
*=-18x^2-3x+24x+4*
*=-18x^2+21x+4*
Note that the image of an element of the product function is equal to multiplying the images of the functions separately. For example, *(fg)(2)=f(2)\cdot g(2):*
*(fg)(2)=-18(2)^2+21(2)+4=-26*
*f(2)\cdot g(2)=[3(2)-4]\cdot [-6(2)-1]=2\cdot (-13)=-26*
Example 2
Find *(f\cdot g)(x)* and its domain if
*f(x)=\dfrac{x}{x^2+2}~~* and *~~g(x)=\dfrac{1}{x-7}*
Solution: in this case, the domain of f is *D_f=\mathbb{R},* because its denominator does not become zero for any real number; the domain of g is *D_g=\mathbb{R}-\{7\}.* Therefore, as the only number they do not share is *x=7, * the domain of fg will exclude that number: *D_{fg}=\mathbb{R}-\{7\}.*
To obtain the function formula, we multiply the two expressions, in this case, we have the multiplication of rational functions and proceed as done with algebraic fractions: multiply numerator with numerator and denominator with denominator.
*(f\cdot g)(x)=f(x)\cdot g(x)*
*=\dfrac{x}{x^2+2}\cdot \dfrac{1}{x-7}*
*=\dfrac{x\cdot 1}{(x^2+2)(x-7)}*
*=\dfrac{x}{x^3-7x^2+2x-14}*
Example 3
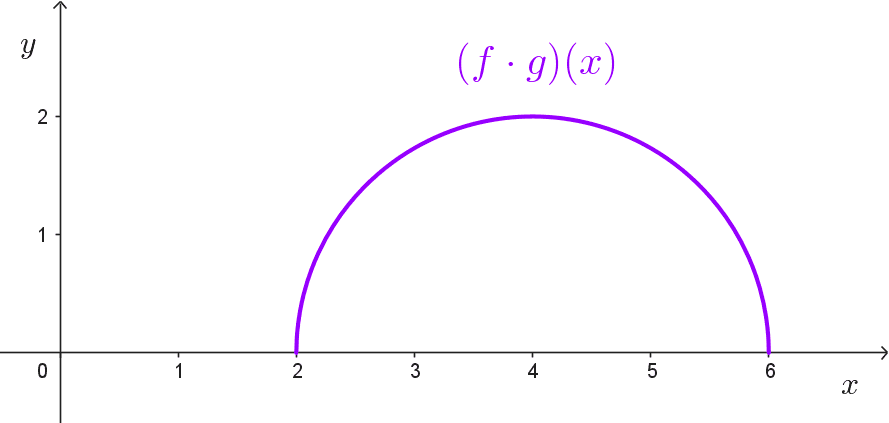
Let *f(x)=\sqrt{x-2}~* and *~g(x)=\sqrt{6-x},* find *(fg)(x)* and its domain.
Solution: the domain of f is *D_f=[2,\infty)* and the domain of g is *D_g=(-\infty, 6].* The domain of fg is then the intersection of these two intervals: *D_{fg}=[2,6].* This interval makes sense because it contains the numbers that belong to both domains simultaneously.
To obtain the equation, we multiply the two expressions, in this case, they are two radical functions and we can use their properties to write a single root:
*(fg)(x)=\sqrt{x-2}\cdot \sqrt{6-x}*
*=\sqrt{(x-2)(6-x)}*
*=\sqrt{6x-x^2-12+2x}*
*=\sqrt{-x^2+8x-12}*
Example 4
If *f(x)=3x^2+6,* calculate *2\cdot f(x).*
Solution: in this case, we want to calculate the multiple of a function. This can be interpreted as multiplying function f by the constant function *g(x)=2.* We obtain it using the formula we know:
*(g\cdot f)(x)=2\cdot f(x)*
*=2\cdot (3x^2+6)*
*=6x^2+12*
Example 5
Let *f(x)=x~* and *~g(x)=\dfrac{1}{x},* find *(f\cdot g)(x)* and its domain.
Solution: the domain of f is *D_f=\mathbb{R},* as it is a polynomial function; the domain of g is *D_g=\mathbb{R}-\{0\},* because *x=0* is the only value that makes its denominator zero. The domain of the product function is the intersection of both domains: *D_{fg}=D_f\cap D_g=\mathbb{R}-\{0\},* because the only value they do not share is *x=0.*
To obtain the equation of the product function, we multiply the formulas of f and g:
*(f\cdot g)(x)=x\cdot \dfrac{1}{x}*
*=\cancel{x}\cdot \dfrac{1}{\cancel{x}}*
*=1*
If we calculate the domain from the final expression, we would have made a mistake because the natural domain of this function is *\mathbb{R}.* However, in our analysis, we determined that the domain of *(fg)(x)* is *\mathbb{R}-\{0\}.* Therefore, it is important to obtain the domain from the intersection of the original domains.
Example 6
If a rectangle has sides *x* and *x-2,* find a function that represents the area of the rectangle for any value of *x.*
Solution: since the area of a rectangle is the product of the lengths of its sides, we can obtain the requested area *A* by multiplying the functions *x* and *x-2:*
*A(x)=x\cdot (x-2)*
*=x^2-2x*
In conclusion, the function representing the area of the rectangle for any value of x is *A(x)=x^2-2x.*
Properties
Function multiplication, like real number multiplication, follows a series of properties which we will see below.
1) Commutativity: the order in which functions are multiplied does not alter the result.
*(f\cdot g)(x)=(g\cdot f)(x)*
2) Associativity: the order in which functions are grouped does not alter the result
*((f\cdot g)\cdot h)(x)=(f\cdot (g\cdot h))(x)*
That is, in a multiplication of three functions, it is the same to multiply the first with the second and then multiply the result with the third, as it is to multiply the second and the third and then multiply the result with the first.
3) Identity element: there exists a function that, when multiplied by another, does not alter the value of the latter. This is the constant function *g(x)=1,* since for any function *f,* it holds that *f(x)\cdot 1=f(x).*
4) Symmetric element: for each function, except zero, there exists another that, when multiplied together, produce a result of 1. For a function *f,* its symmetric element is *1/f,* because *f(x)\cdot \dfrac{1}{f(x)}=1.* The symmetric function should not be confused with the inverse function. For example, if *f(x)=2x,* its symmetric function is *g(x)=\dfrac{1}{2x},* because *2x\cdot \dfrac{1}{2x}=1.* It is important to note that the symmetric function does not exist where the original function is zero.
5) Distributivity: function multiplication can be distributed with respect to the sum or difference of functions
*(f\cdot (g+h))(x)=(fg)(x)+(fh)(x)*
Practice exercises
Exercise: for each pair of functions obtain *f\cdot g* and its domain.
- *f(x)=2x-3,~~ g(x)=3x+5*
- *f(x)=\sqrt{x+1},~~ g(x)=\dfrac{2}{x}*
- *f(x)=\dfrac{1}{x-2},~~ g(x)=\dfrac{x^2}{x+5}*
Solutions:
- *(f\cdot g)(x)=6x^2+x-15,* *~~~D=\mathbb{R}*
- *(f\cdot g)(x)=\dfrac{2\sqrt{x+1}}{x},* *~~~D=[-1,0)\cup (0,\infty]*
- *(f\cdot g)(x)=\dfrac{x^2}{x^2+3x-10},* *~~~D=\mathbb{R}-\{-5;2\}*
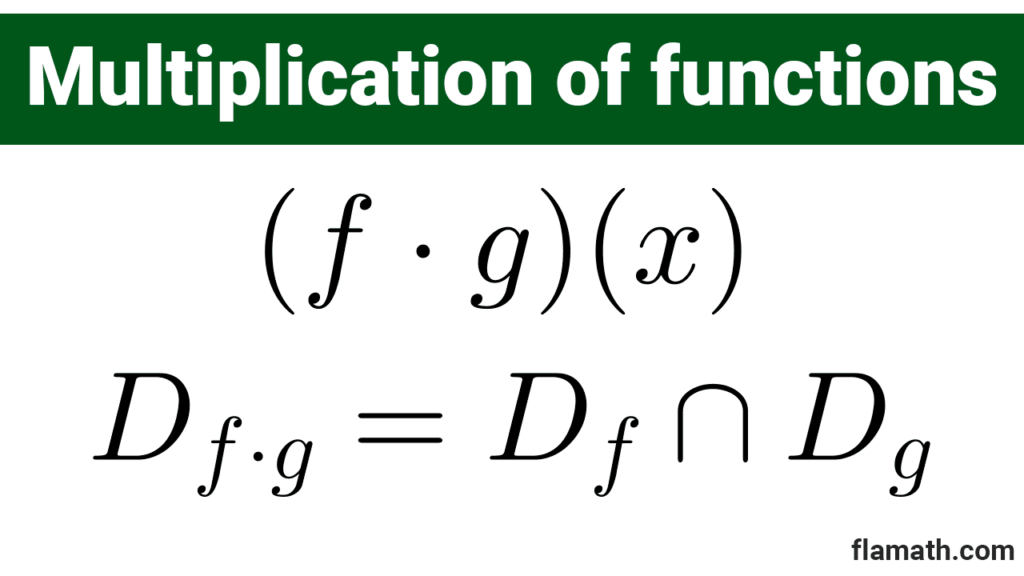
Other articles that may interest you