Squeeze Theorem

In this article we study an important and well-known theorem on limits that allows the simplest calculation of others: the squeeze or sandwich theorem. Also, we will see some examples of its application.

Table of Contents

Statement of the theorem

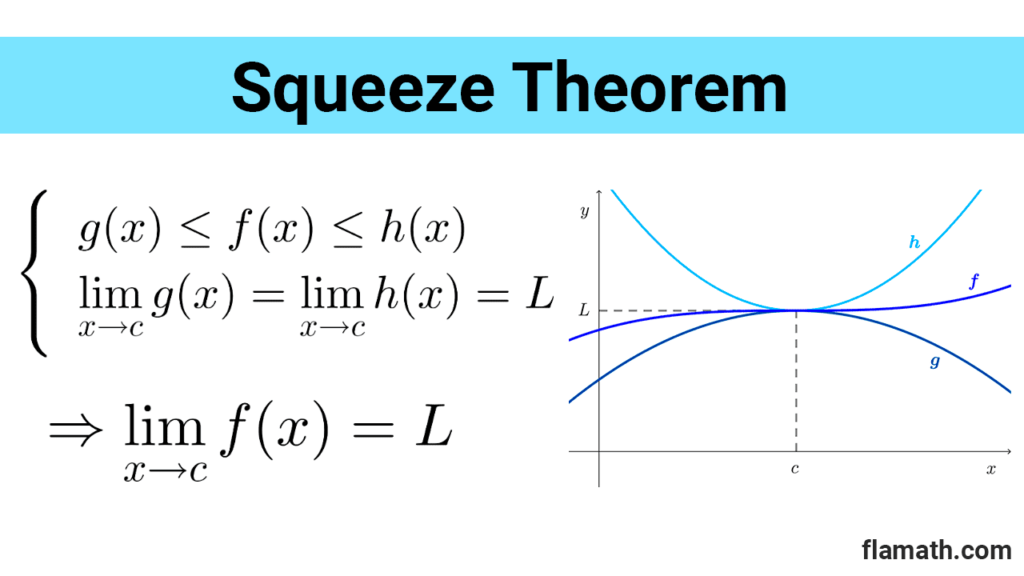
The squezze theorem (or sandwich theorem) tells us that if a function is trapped between two other functions near a point, and these two functions have the same limit at the point, then the first function is forced to have the same limit at the point.

Squeeze Theorem: If *g(x)≤f(x)≤h(x)* as x is close to c (except possibly at c), and the limits of g and h at c exist and are equal to L, *\lim_{x\to c} g(x)=\lim_{x\to c} h(x)=L,* then the limit of f at c also exists and is equal to L:

$$\lim_{x\to c} f(x)=L$$

Explanatory graph of the squeeze / sandwich theorem of limits — Squeeze Theorem

This theorem is very useful when calculating limits, including the fundamental trigonometric limit.

Examples of application of the sandwich theorem

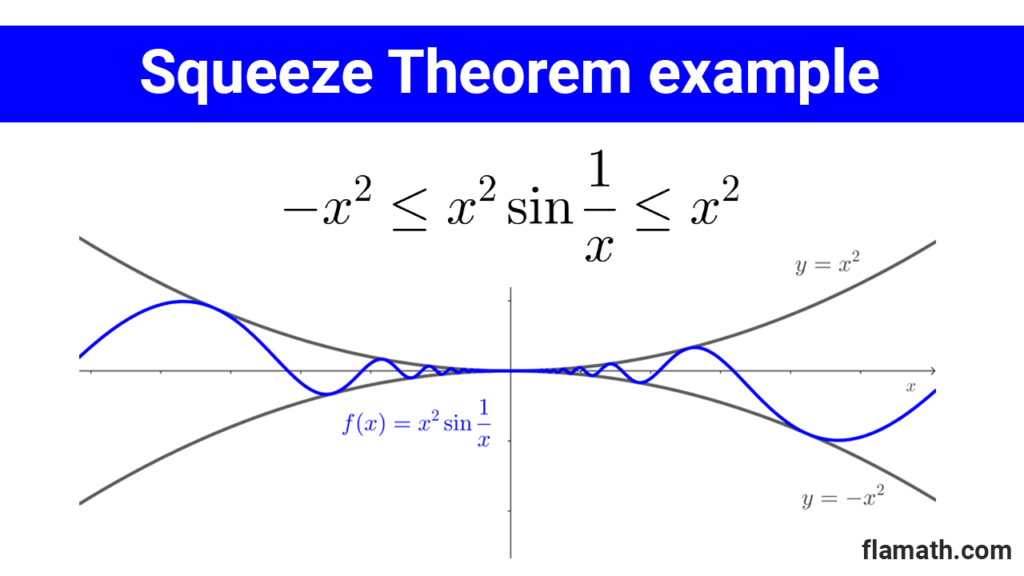
Example 1: Find *\lim_{x\to 0} x^2 \sin \dfrac{1}{x}*

Solution: First, observe that we cannot use the product property, as this would give

*\lim_{x\to 0} x^2 \sin(1/x)=\lim_{x\to 0} x^2\cdot \lim_{x\to 0} \sin(1/x),* but *\lim_{x\to 0} \sin(1/x)* does not exist.

Instead of this, we can apply the squeeze theorem, and therefore, we need to find a function g smaller than *f(x)=x^2 \sin(1/x)* and a function h greater than f such that g and h have the same limit at zero. Since we know that the sine function is between -1 and 1, we can write:

*-1≤\sin \dfrac{1}{x}≤1*

Any inequality remains true when multiplied by a positive number. We know that *x^2≥0* for all x, and therefore, by multiplying each side of the above inequalities by *x^2*, we get:

*-x^2≤x^2 \sin \dfrac{1}{x}≤x^2*

In other words, *-x^2≤f(x)≤x^2*

We know that *\lim_{x\to 0} x^2=0* and *\lim_{x\to 0} (-x^2)=0.*

Taking *g(x)=-x^2* and *h(x)=x^2,* by the squeeze theorem, we have

$$\lim_{x\to 0} x^2 \sin \dfrac{1}{x}=0$$

Example 1 of the squeeze theorem — Graph of the example function enclosed between the graphs of g and h.

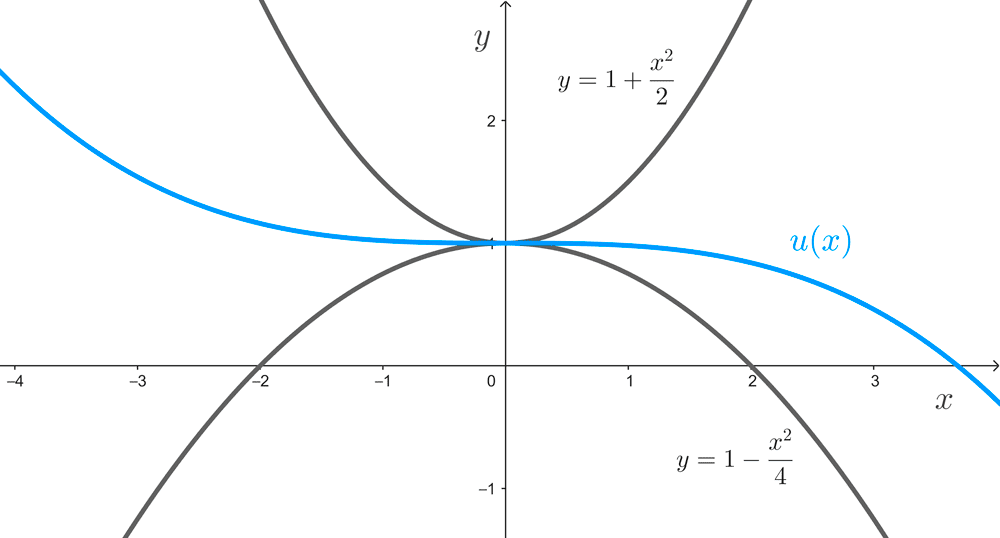
Example 2: Find *\lim_{x\to 0} u(x)* being *u* a function such that:

*1-\dfrac{x^2}{4}≤u(x)≤1+\dfrac{x^2}{2}* for all *x≠0.*

Solution: As *\lim_{x\to 0} \left(1-\dfrac{x^2}{4}\right)=1* and *\lim_{x\to 0} \left(1+\dfrac{x^2}{2}\right)=1,* applying the squeeze theorem leads us to: $$\lim_{x\to 0} u(x)=1$$

Example 2 of the squeeze theorem — Graph of the functions from example 2

Note that no matter how complicated the function u is, as long as the initial conditions are met, its limit at zero will be equal to one.

Daniel Machado

Advanced student of Mathematics at Facultad de Ciencias Exactas, Químicas y Naturales. Universidad Nacional de Misiones, Argentina.