
Limit laws
In this article we explain the properties of the limit of a function and how to apply them to solve problems.
Table of Contents
Properties of limits
Limits in calculus follow a number of properties that can be applied to find them more quickly. Below, we will explore some involving operations between functions.
Suppose k is a constant and the limits *\lim_{x\to a} f(x)* and *\lim_{x\to a} g(x)* exist; then the following properties hold.
Sum rule: the limit of the sum is equal to the sum of the limits.
$$\lim_{x\to a} [f(x)+g(x)]=\lim_{x\to a} f(x) + \lim_{x\to a} g(x)$$
Difference rule: the limit of a difference is equal to the difference of the limits.
$$\lim_{x\to a} [f(x)-g(x)]=\lim_{x\to a} f(x) - \lim_{x\to a} g(x)$$
Constant multiple rule: the limit of a constant times a function is equal to the constant times the limit of the function.
$$\lim_{x\to a} [k\cdot f(x)]=k\cdot \lim_{x\to a} f(x)$$
Product rule: the limit of a product is equal to the product of the limits.
$$\lim_{x\to a} [f(x)\cdot g(x)]=\lim_{x\to a} f(x)\cdot \lim_{x\to a} g(x)$$
Quotient rule: the limit of a quotient is equal to the quotient of the limits, provided that the limit of the denominator is not zero.
$$\lim_{x\to a} \dfrac{f(x)}{g(x)}=\dfrac{\lim_{x\to a} f(x)}{\lim_{x\to a} g(x)}$$
provided that *\lim_{x\to a} g(x)≠0*
Power rule: the limit of a function raised to a positive integer power is equal to the limit raised to the power.
$$\lim_{x\to a} [f(x)]^n=[\lim_{x\to a} f(x)]^n$$
where n is a positive integer.
Root rule: the limit of a root of a function is equal to the root of the limit.
$$\lim_{x\to a} \sqrt[n]{f(x)}=\sqrt[n]{\lim_{x\to a} f(x)}$$
n is a positive integer. If n is even, assume *\lim_{x\to a} f(x)>0*
All these properties are also applicable to one-sided limits if they exist.
Limits of Elementary Functions
Here are some well-known limits of functions commonly used.
Limit of a Constant Function: *\lim_{x\to a} k=k*
Limit of the Identity Function: *\lim_{x\to a} x=a*
Limit of a Power Function: *\lim_{x\to a} x^n=a^n,* where n is a positive integer.
Limit of a Root Function: *\lim_{x\to a} \sqrt[n]{x}=\sqrt[n]{a},* where n is a positive integer, and if n is even, assume *a>0*
These known properties and limits are useful for calculating limits, allowing us to "break down" limits into simpler ones. We will work with some examples below.
Example 1: Evaluate the following limit *\lim_{x\to 5} (2x^2-3x+4)*
Solution:
*\lim_{x\to 5} (2x^2-3x+4)=\lim_{x\to 5} (2x^2)-\lim_{x\to 5} (3x)+\lim_{x\to 5} 4~~* (sum and difference rule)
*=2 \lim_{x\to 5} x^2-3 \lim_{x\to 5} x+\lim_{x\to 5} 4~~* (constant multiple rule)
*=2 (5^2)-3 (5)+4~~* (limits of power function, identity, and constant)
*=39*
Note that if we define *f(x)=2x^2-3x+4,* then *f(5)=39.* In other words, we would have obtained the correct answer by substituting *x* with *5.*
Example 2: Determine the following limit *\lim_{x\to -2} \dfrac{x^3+2x^2-1}{5-3x}*
Solution: we start by using the quotient rule; its use is justified because, in the end, we determine that the limits exist and that the denominator is not zero. Otherwise, it could not be used.
*\lim_{x\to -2} \dfrac{x^3+2x^2-1}{5-3x}=\dfrac{\lim_{x\to -2} (x^3+2x^2-1)}{\lim_{x\to -2} (5-3x)}*
*=\dfrac{\lim_{x\to -2} (x^3)+\lim_{x\to -2} (2x^2)-\lim_{x\to -2}1)}{\lim_{x\to -2} 5-3 \lim_{x\to -2} x}~~*(sum and difference rule)
*=\dfrac{\lim_{x\to -2} (x^3)+2 \lim_{x\to -2} x^2-\lim_{x\to -2}1)}{\lim_{x\to -2} 5-3 \lim_{x\to -2} x}~~* (constant multiple rule)
*=\dfrac{(-2)^3+2(-2)^2-1}{5-3(-2)}~~* (limits of power function, identity, and constant)
*=-\dfrac{1}{11}*
Note that if we define *f(x)= \dfrac{x^3+2x^2-1}{5-3x},* then *f(-2)=-\dfrac{1}{11}.* Similarly to the previous example, we would have obtained the limit by substituting *x* with *-2* in the function formula.
Direct substitution property
What we saw in the previous examples is an illustration of the following property, which makes it easier to calculate limits of polynomial and rational functions.
It is possible to use the sum, power, and constant multiple rules to calculate the limit of a general polynomial function.
If *P(x)=a_n x^n+a_{n-1} x^{n-1}+...+a_1 x+a_0* is a polynomial function. Then:
*\lim_{x\to c} P(x)=\lim_{x\to c} (a_n x^n+a_{n-1} x^{n-1}+...+a_1 x+a_0)*
*=\lim_{x\to c} a_n x^n+\lim_{x\to c} a_{n-1} x^{n-1}+...+\lim_{x\to c} a_1 x+\lim_{x\to c} a_0*
*=a_n \lim_{x\to c} x^n+a_{n-1} \lim_{x\to c} x^{n-1}+...+a_1 \lim_{x\to c} x+a_0*
*=a_n c^n+a_{n-1} c^{n-1}+...+a_1 c+a_0*
*=P(c)*
So, to calculate the limit of a polynomial function *f* as x approaches a real number c, you only need to evaluate the function at c, in other words, substitute x with c in the function formula.
$$\lim_{x\to c} P(x)=P(c)$$
Considering that a rational function is nothing more than a quotient of polynomial functions, it suffices to apply the quotient rule and the ones we used earlier to reach the conclusion that the same thing happens as we just saw: to find the limit at a point, you have to evaluate the function at that point. Since we have applied the quotient rule, it is important that the denominator is not zero.
If *P(x)* and *Q(x)* are polynomial functions, then:
$$\lim_{x\to c} \dfrac{P(x)}{Q(x)}=\dfrac{P(c)}{Q(c)}$$
provided that *Q(c)≠0*
Direct substitution property
If *f* is a polynomial or rational function and c is in the domain of *f,* then:
$$\lim_{x\to c} f(x)=f(c)$$
Direct substitution can also be applied to calculate limits of trigonometric functions.
Examples of application of properties
Example 1: Find *\lim_{x\to -1} \dfrac{x^3+4x^2-3}{x^2+5}*
Solution: We could use the direct substitution property; for this, we must ensure that the denominator is not zero at the point of interest: if *Q(x)=x^2+5,* *Q(-1)=6≠0;* therefore, we can perform the substitution.
*\lim_{x\to -1} \dfrac{x^3+4x^2-3}{x^2+5}=\dfrac{(-1)^3+4(-1)^2-3}{(-1)^2+5}*
*=\dfrac{0}{6}*
*=0*
Example 2: Find *\lim_{x\to -2} \sqrt{-5x^3-4x^2+1}*
Solution: We can apply the square root rule with *n=2.* Then, the limit "enters" the root. Considering that the function of the radicand is polynomial, we can apply direct substitution.
*\lim_{x\to -2} \sqrt{-5x^3-4x^2+1}=\sqrt{\lim_{x\to -2} (-5x^3-4x^2+1)}*
*=\sqrt{-5(-2)^3-4(-2)^2+1}*
*=\sqrt{25}*
*=5*
Properties of infinite limits
Infinite limits have some special properties that we will see below.
Let c and L be real numbers, and let f and g be functions such that
$$\lim_{x\to c} f(x)=\infty~~\text{and}~~ \lim_{x\to c} g(x)=L$$
Sum or difference:
$$\lim_{x\to c} [f(x)+g(x)]=\infty$$
$$\lim_{x\to c} [f(x)-g(x)]=\infty$$
Product:
$$\lim_{x\to c} [f(x) g(x)]=\infty~~\text{if}~L>0$$
$$\lim_{x\to c} [f(x) g(x)]=-\infty~~\text{if}~L<0$$
Quotient:
$$\lim_{x\to c} \dfrac{g(x)}{f(x)}=0$$
$$\lim_{x\to c} \dfrac{f(x)}{g(x)}=\infty~~\text{if}~L>0$$
$$\lim_{x\to c} \dfrac{f(x)}{g(x)}=-\infty~~\text{if}~L<0$$
Similar properties are valid for one-sided limits and for functions whose limit as x approaches c is *-\infty*
Example 1: Since *\lim_{x\to 0} 1=1* and *\lim_{x\to 0} \dfrac{1}{x^2}=\infty,* it follows that
*\lim_{x\to 0} \left(1+\dfrac{1}{x^2}\right)=\infty*
Example 2: From *\lim_{x\to 1} (x^2+1)=2* and *\lim_{x\to 1^-} \dfrac{1}{x-1}=-\infty,* we deduce that
*\lim_{x\to 1^-} \dfrac{x^2+1}{1/(x-1)}=0*
Example 3: As *\lim_{x\to 0} 3=3* and *\lim_{x\to 0} \cot x=\infty,* we have
*\lim_{x\to 0} 3 \cot x=\infty*
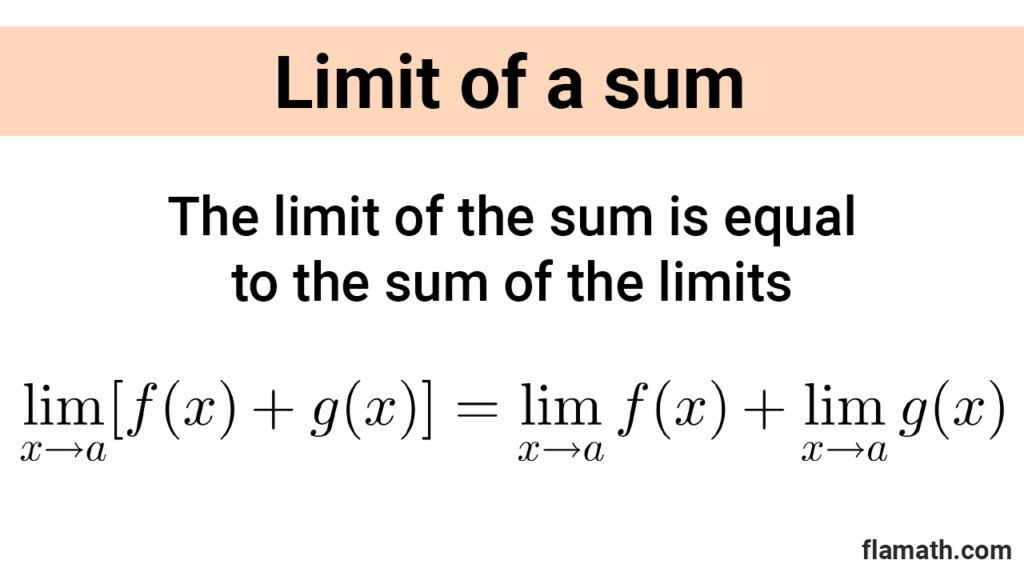
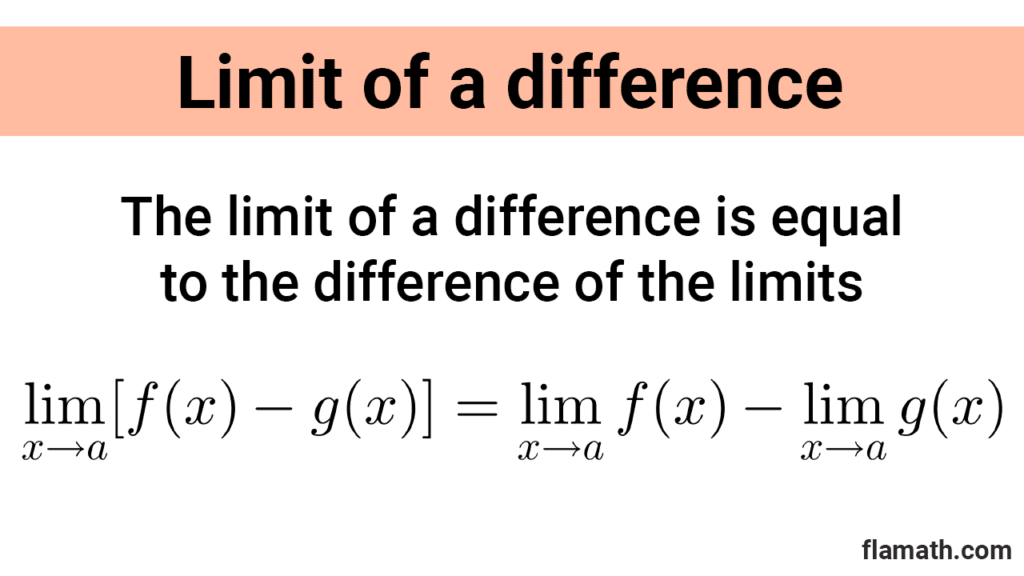



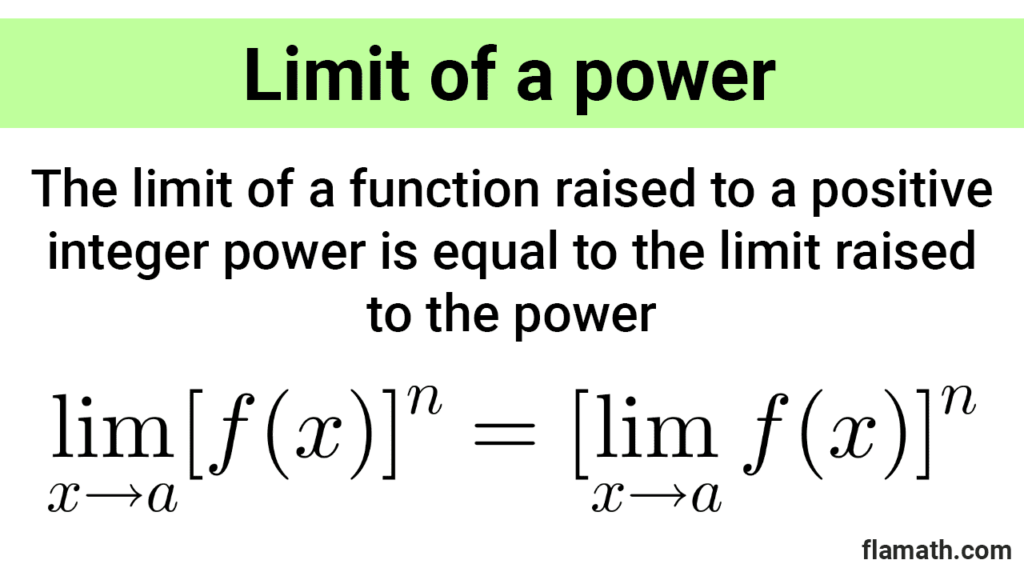



Other articles that may interest you