
Limit theorems
In this article we study important theorems about limits of functions that are useful when calculating them.
Table of Contents
Existence and uniqueness theorems
Existence of the limit: Let *f* be a real function, and *c* a point that may or may not be in its domain. The limit of *f* at *c* exists if and only if the one-sided limits at *c* exist and are equal. Symbolically:
*\lim_{x\to c} f(x)=L ↔ \lim_{x\to c^+} f(x)=\lim_{x\to c^-} f(x)=L*
Uniqueness of the limit: If *f* is a real function and the limit of *f* at a point *c* exists, then this limit is unique. Symbolically:
*\lim_{x\to c} f(x)=L~~and~~\lim_{x\to c} f(x)=M → L=M*
Limits of functions operations
Suppose *k* is a constant, *n* is a positive integer, and the limits *\lim_{x\to a} f(x)* and *\lim_{x\to a} g(x)* exist. Then, the following properties hold.
$$\lim_{x\to a} [f(x)+g(x)]=\lim_{x\to a} f(x) + \lim_{x\to a} g(x)$$
$$\lim_{x\to a} [f(x)-g(x)]=\lim_{x\to a} f(x) - \lim_{x\to a} g(x)$$
$$\lim_{x\to a} [k\cdot f(x)]=k\cdot \lim_{x\to a} f(x)$$
$$\lim_{x\to a} [f(x)\cdot g(x)]=\lim_{x\to a} f(x)\cdot \lim_{x\to a} g(x)$$
$$\lim_{x\to a} \dfrac{f(x)}{g(x)}=\dfrac{\lim_{x\to a} f(x)}{\lim_{x\to a} g(x)}~~~(\text{provided}~\lim_{x\to a} g(x)≠0)$$
$$\lim_{x\to a} [f(x)]^n=[\lim_{x\to a} f(x)]^n$$
$$\lim_{x\to a} \sqrt[n]{f(x)}=\sqrt[n]{\lim_{x\to a} f(x)}$$
If *n* is even, let's assume that *\lim_{x\to a} f(x)>0*
Limits of elemental functions
If *f(x)=k* and a is in its domain, then *\lim_{x\to a} f(x)=\lim_{x\to a} k=k*
If *f(x)=x* and a is in its domain, then *\lim_{x\to a} x=a*
If *f(x)=x^n* where *n* is a positive integer and a is in its domain, then *\lim_{x\to a} x^n=a^n*
If *f(x)=\sqrt[n]{x}* where *n* is a positive integer and a is in its domain, then *\lim_{x\to a} \sqrt[n]{x}=\sqrt[n]{a}.* If *n* is even, we assume *a>0*
Limit of a composite function: If *f* and *g* are two functions such that *\lim_{x\to a} g(x)=L* and *\lim_{x\to L} f(x)=f(L),* then $$\lim_{x\to a} f(g(x))=f(\lim_{x\to a} g(x))=f(L)$$
Direct substitution theorem
If *f* is a polynomial, rational, or trigonometric function, and *c* is in the domain of *f*, then:
$$\lim_{x\to c} f(x)=f(c)$$
This theorem states that the limit of the mentioned functions at a point in their domain is equal to the value of the function at that point.
Other important theorems
Theorem: If *f(x)≤g(x)* when x is close to c (except possibly at c), and the limits of *f* and *g* exist as x approaches c, then:
$$\lim_{x\to c} f(x)≤\lim_{x\to c} g(x)$$
This theorem indicates that if the values of a function f remain below or equal to those of another function g near a point, then the limit of f at c also remains below or equal to the limit of g at the same point, provided both limits exist.
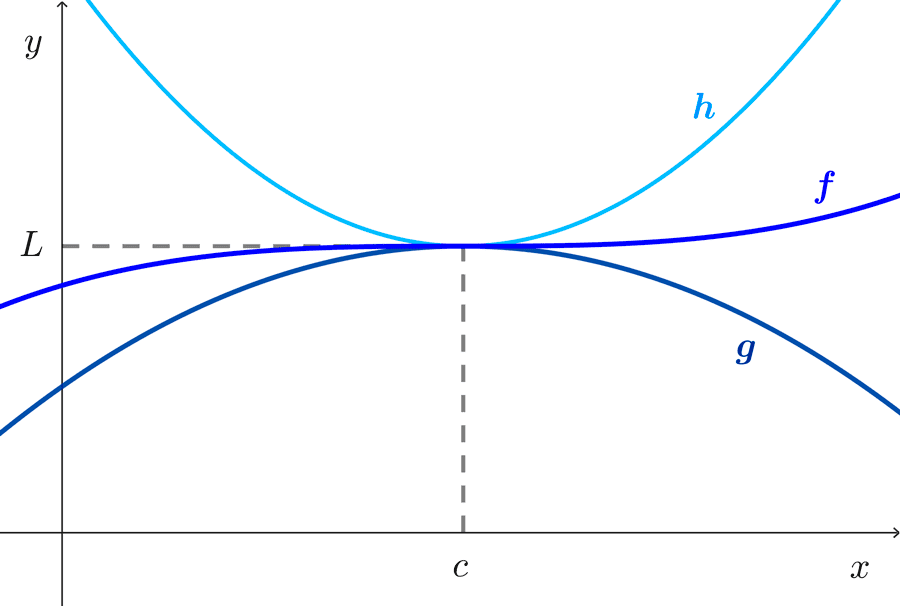
Squeeze Theorem: If *g(x)≤f(x)≤h(x)* when x is close to c (except possibly at c), and *\lim_{x\to c} g(x)=\lim_{x\to c} h(x)=L,* then:
$$\lim_{x\to c} f(x)=L$$
The Squeeze Theorem states that if *f(x)* is trapped between *g(x)* and *h(x)* near c, and if both g and h have the same limit L at c, then f is forced to have the same limit L at c.
This theorem is useful for calculating many limits, including the fundamental trigonometric limit.



Other articles that may interest you