How to find the Axis of Symmetry of a quadratic function
This article is a guide to find the axis of symmetry of a quadratic function with step-by-step exercises.
Table of Contents
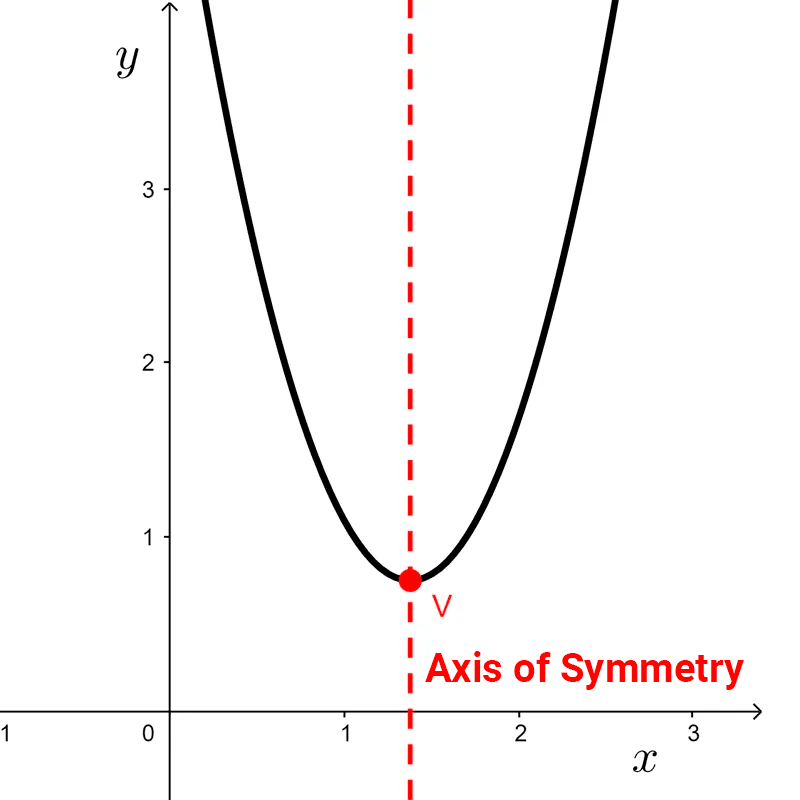
What is the axis of symmetry?
The axis of symmetry of a quadratic function is the vertical line that divides the parabola into two equal parts.
Equation of the axis of symmetry
Let *f(x)=ax^2+bx+c* be the quadratic function, the axis of symmetry of the graph of this function has the equation:
*x=\dfrac{-b}{2a}*
This expression becomes familiar after working with the vertex, as it is the x-coordinate of the same. This is because the axis of symmetry passes through the vertex. So, having found the vertex *V=(h, k)* makes it easier for us to determine the axis of the parabola, since its equation is simply *x=h.*
In summary, to calculate the axis of symmetry of a quadratic function, we must substitute the coefficient values into the formula x=-b/2a, which is the equation of the axis.
Solved exercises
Exercise 1: Find the axis of symmetry of the function *f(x)=-2x^2+8x-5*
Solution:
Identify the coefficients to be used: *a=-2, b=8* and substitute them into the formula:
*x=\dfrac{-b}{2a}=\dfrac{-8}{2(-2)}=\dfrac{-8}{-4}=2*
Therefore, the equation of the axis of symmetry of the function is *x=2*
Exercise 2: Determine the equation of the axis of symmetry of the function *f(x)=x^2+x+7*
Solution:
Extract the coefficients needed to calculate: *a=1, b=1* and substitute them into the formula:
*x=\dfrac{-b}{2a}=\dfrac{-1}{2(1)}=-\dfrac{1}{2}*
Therefore, the equation of the axis of symmetry of the function is *x=-\dfrac{1}{2}*
Exercise 3: Calculate the axis of symmetry of the function *f(x)=-x^2+1*
Solution:
Recognize the coefficients: *a=-1, b=0* and substitute them into the formula:
*x=\dfrac{-b}{2a}=\dfrac{-0}{2(-1)}=0*
The equation of the axis of symmetry of the function is *x=0.* In this case, it coincides with the y-axis.
Exercise 4: Obtain the equation of the axis of symmetry of the function *f(x)=7x^2-3*
Solution:
Locate the coefficients needed: *a=7, b=0* and substitute them into the formula:
*x=\dfrac{-b}{2a}=\dfrac{-0}{2\cdot7}=0*
The equation of the axis of symmetry of the function is *x=0.* As in the previous exercise, it coincides with the y-axis.


Other articles that may interest you