Find quadratic function from vertex and point
In this article we explain how to find a quadratic function if we know the vertex and a point of it.
Table of Contents
Deduction of the procedure
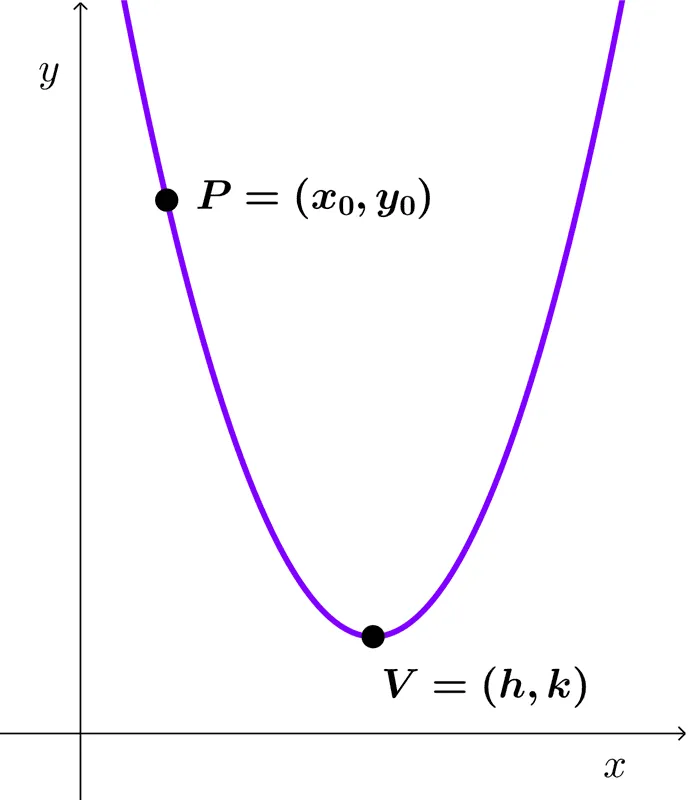
We seek to find the quadratic function whose vertex is *V=(h,k)* and passes through the point *P=(x_0,y_0)*
We can use the vertex form and complete it with the given data:
*f(x)=a(x-h)^2+k*
We need to determine the value of *a*
Since the function passes through the point *P,* we have *f(x_0)=y_0,* i.e.,
*f(x_0)=a(x_0-h)^2+k=y_0*
From here, we can solve for *a*
*a=\dfrac{y_0-k}{(x_0-h)^2}*
It is not necessary to memorize these formulas, as understanding the logic is sufficient to work through the exercises. However, it allows us to outline the general solution procedure.
How to Find a Quadratic Function Given Its Vertex and a Point
- Replace the coordinates of the vertex in the vertex form of the function.
- Replace the data of the other point and solve for the number a.
- Rewrite the vertex form with the new data.
- Expand, if necessary, to find the polynomial form of the function.
Solved exercises
Exercise 1: Find the quadratic function with vertex *V=(5,7)* that passes through the point *P(-7,1)*
Solution:
Replace the vertex data into the vertex form: *h=5,k=7*
*f(x)=a(x-h)^2+k*
*f(x)=a(x-5)^2+7*
Now use the data from point *P,* knowing that *f(-7)=1*
*f(-7)=a(-7-5)^2+7=1*
Solve for *a:*
*a(-12)^2+7=1→a=\dfrac{1-7}{(-12)^2}=\dfrac{-6}{144}=-\dfrac{1}{24}*
With this new data, we have enough to find the function, which is:
*f(x)=-\dfrac{1}{24}(x-5)^2+7*
Expanding further, we can arrive at the general form if needed:
*f(x)=-\dfrac{x^2}{24}+\dfrac{5x}{12}+\dfrac{143}{24}*
Exercise 2: Determine the rule of the quadratic function with vertex *V=(-1,-3)* that passes through the point *(4,9)*
Solution:
Use the vertex data for the vertex form: *h=-1, k=-3*
*f(x)=a(x-(-1))^2+(-3)*
*f(x)=a(x+1)^2-3*
Now use the data from the other point to find the value of *a,* knowing that *f(4)=9*
*f(4)=a(4+1)^2-3=9*
*a(5)^2-3=9→a=\dfrac{9+3}{5^2}=\dfrac{12}{25}*
Now you can write the formula for the function:
*f(x)=\dfrac{12}{25}(x+1)^2-3*
Exercise 3: Determine the quadratic function whose vertex is *(-1,5)* and intersects the y-axis at *-3*
Solution:
The graph intersects the vertical axis at *y=-3,* meaning the point *(0,-3)* lies on the graph.
Substitute the vertex data into the vertex form: *h=-1, k=5*
*f(x)=a(x-(-1))^2+5*
*f(x)=a(x+1)^2+5*
Now use the other data, knowing that *f(0)=-3*
*f(0)=a(0+1)^2+5=-3*
*a(1)^2+5=-3→a=\dfrac{-3-5}{1}=-8*
With this information, you can find the function's formula:
*f(x)=-8(x+1)^2+5*



Other articles that may interest you