Positive and negative intervals of quadratic functions

In this article we explain the intervals of positivity and negativity of a quadratic function and how to calculate them depending on each case.

Table of Contents

Positive and negative functions

A function *f* is positive on an interval *I* if *f(x)>0* for every *x* in *I.* It is negative on *I* if *f(x)<0* for every *x* in *I.* Geometrically, the positive part of a function is located above the x-axis, and the negative part is below.

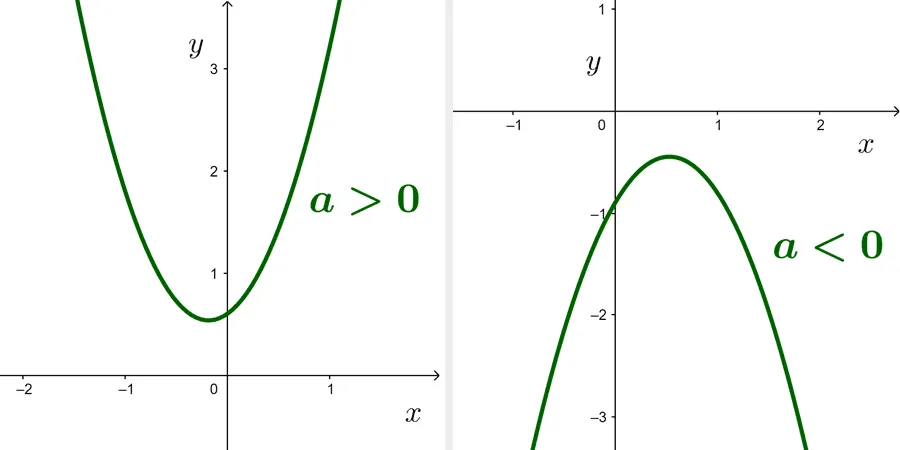
Our focus is on discovering intervals where a quadratic function is positive or negative. It is evident from the graph that if it does not touch the x-axis, it will be either entirely negative or entirely positive, depending on whether the parabola opens downward or upward:

quadratic function with graph opening upward or downward — If *a>0*, the function is positive over its entire domain. If *a<0*, it is negative over the entire domain.

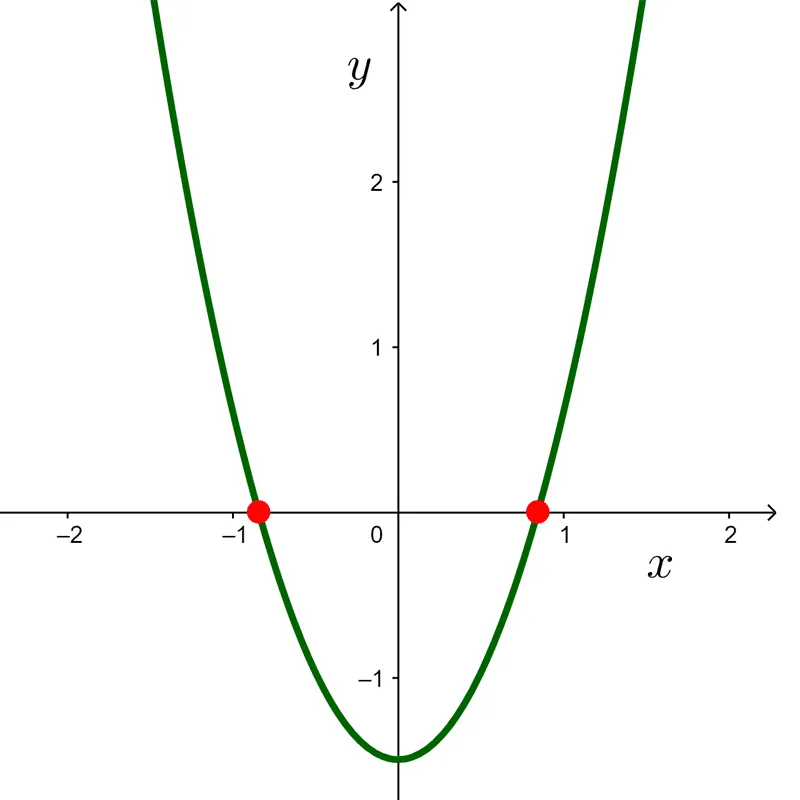
However, if the function has a real zero, it will touch the x-axis at one point, and in all other points of the domain, it will be positive or negative similarly to the previous case:

Remember that if a quadratic function does not touch the x-axis, it is because its discriminant is negative. If it touches the x-axis at one point, the discriminant is zero.

Let *f(x)=ax^2+bx+c,* if *Δ<0,* then:

If *a>0,* the function is positive over *\mathbb{R}*
If *a<0,* the function is negative over *\mathbb{R}*

If *Δ=0* and *x_1* is the real zero of *f,* then:

If *a>0,* the function is positive over *\mathbb{R}-\{x_1\}*
If *a<0,* the function is negative over *\mathbb{R}-\{x_1\}*

Now, suppose the discriminant is positive. The graph will touch the x-axis at two points, allowing the existence of intervals where the function is positive and others where it is negative.

There exists a part of the domain where the quadratic function is positive and another where it is negative. — There exists a part of the domain where the function is positive and another where it is negative.

To find these intervals, we need to know the zeros of the function and have it written in factored form.

First case: parabola opens upward, a>0

*f(x)=a(x-x_1)(x-x_2)*

Positive Interval

We must find the values where *f(x)* is greater than zero, that is,

*a(x-x_1)(x-x_2)>0*

Dividing both sides by *a,* since it is positive, the inequality sign remains the same:

*(x-x_1)(x-x_2)>0*

Two options can occur, either both factors are positive or both are negative. In both cases, their product yields a positive number.

1. If both are positive: *(x-x_1)>0∧(x-x_2)>0→(x>x_1)∧(x>x_2)*

These conditions are equivalent to the intersection of these intervals:

*(x_1,+∞)\cap(x_2,+∞)=(x_2,+∞)*

2. If both are negative: *(x-x_1)<0∧(x-x_2)<0→(x<x_1)∧(x<x_2)*

*(-∞,x_1)\cap(-∞,x_2)=(-∞,x_1)*

Therefore, the function is positive in the interval: *C^{+}=(-∞,x_1)\cup(x_2,+∞)*

Negative Interval

*a(x-x_1)(x-x_2)<0*

*(x-x_1)(x-x_2)<0*

It can happen that the first factor is positive and the other negative, or vice versa.

1. *(x-x_1)<0∧(x-x_2)>0→(x<x_1)∧(x>x_2)*

*(-∞,x_1)\cap(x_2,+∞)=ϕ*

2. *(x-x_1)>0∧(x-x_2)<0→(x>x_1)∧(x<x_2)*

*(x_1,+∞)\cap(-∞,x_2)=(x_1,x_2)*

So, the function is negative in the interval *C^{-}=ϕ\cup(x_1,x_2)=(x_1,x_2)*

The quadratic function *f(x)=ax^2+bx+c* where *a>0* and its zeros are *x_1* and *x_2,* and *x_1<x_2,* is positive in the interval:

*C^{+}=(-∞,x_1)\cup(x_2,+∞)*

and is negative in the interval:

*C^{-}=(x_1,x_2)*

Between the roots, the graph of the quadratic function is below the x-axis (negative), and in the rest of the domain, it is above (positive). — Between the zeros, the graph of the function is below the x-axis (negative), and in the rest of the domain, it is above (positive).

Second case: parabola opens downward, a<0

*f(x)=a(x-x_1)(x-x_2)*

Positive Interval

*a(x-x_1)(x-x_2)>0*

Dividing both sides by *a,* since it is negative, reverses the inequality sign:

*(x-x_1)(x-x_2)<0*

Previously, we deduced that this occurs in the interval *(x_1,x_2)*

Negative Interval

*a(x-x_1)(x-x_2)<0*

*(x-x_1)(x-x_2)>0*

As seen before, this occurs in the interval *(-∞,x_1)\cup(x_2,+∞)*

The quadratic function *f(x)=ax^2+bx+c* where *a<0* and its zeros are *x_1* and *x_2* with *x_1<x_2,* is positive in the interval:

*C^{+}=(x_1,x_2)*

and is negative in the interval:

*C^{-}=(-∞,x_1)\cup(x_2,+∞)*

Between the roots, the graph of the quadratic function is above the x-axis (positive), and in the rest of the domain, it is below (negative). — Between the zeros, the graph is above the x-axis (positive), and in the rest of the domain, it is below (negative).

Solved exercises

Exercise 1: Find the intervals where the function *f(x)=2x^2+2x-4* is positive or negative.

Solution:

Find the zeros of the function:

*x_1=-2*

*x_2=1*

Since *a=2* is positive, we are in the first case, so:

Positive interval: *C^{+}=(-∞,-2)\cup(1,+∞)*

Negative interval: *C^{-}=(-2,1)*

We could have also determined these intervals from the factored form (as done in the deduction) or from the graph of the function.

Exercise 2: Find the intervals of positivity and negativity for the function *f(x)=-2x^2+28x-90*

Solution:

Calculate the zeros of the function:

*x_1=5*

*x_2=9*

Since *a=-2* is negative, we are in the second case. So:

Positive interval: *C^{+}=(5,9)*

Negative interval: *C^{-}=(-∞,5)\cup(9,+∞)*

Exercise 3: Determine in which intervals the function *f(x)=-9x^2-72x-63* is positive or negative.

Solution:

First, determine the zeros:

*x_1=-7*

*x_2=-1*

Since *a=-9* is negative, we are in the second case:

Positive interval: *C^{+}=(-7,-1)*

Negative interval: *C^{-}=(-∞,-7)\cup(-1,+∞)*

Daniel Machado

Advanced student of Mathematics at Facultad de Ciencias Exactas, Químicas y Naturales. Universidad Nacional de Misiones, Argentina.