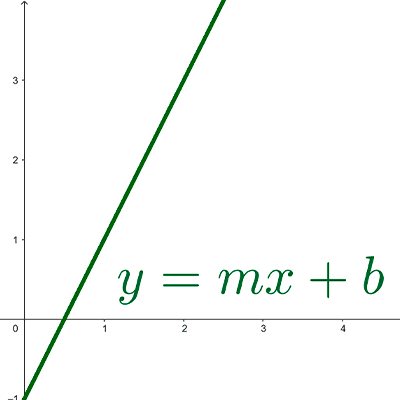Aprende sobre funciones y lógica matemática
Descubre una amplia gama de recursos matemáticos diseñados para ayudarte a aprender matemáticas de manera efectiva. Desde lecciones hasta ejercicios, aplicaciones, demostraciones y mucho más, nuestro principal objetivo es potenciar tus habilidades matemáticas y hacerte disfrutar de esta fascinante ciencia.
Funciones
Una función es una regla que asigna a cada número real del conjunto, llamado dominio, un único número real de otro conjunto, llamado codominio.

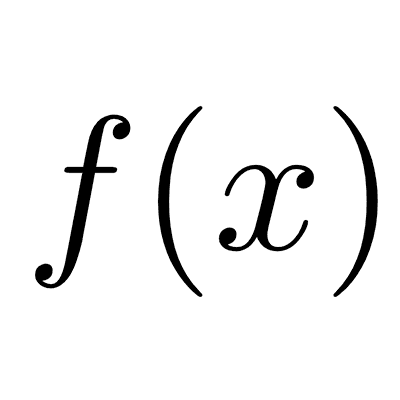
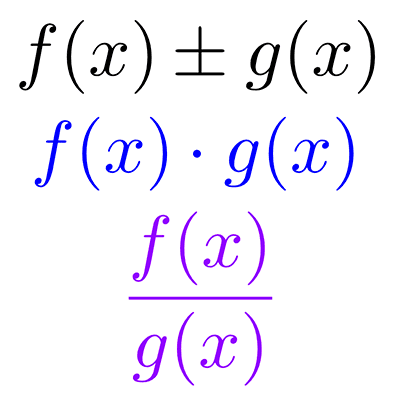
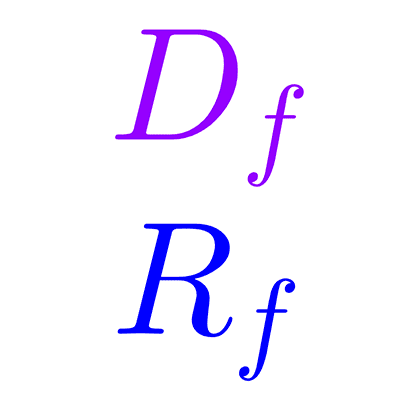
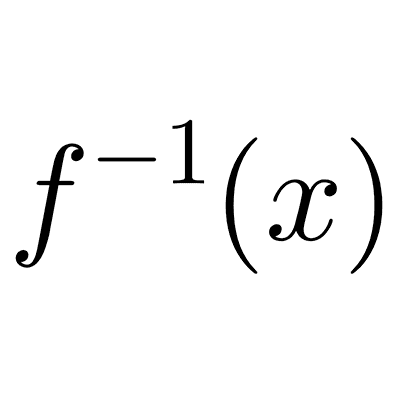

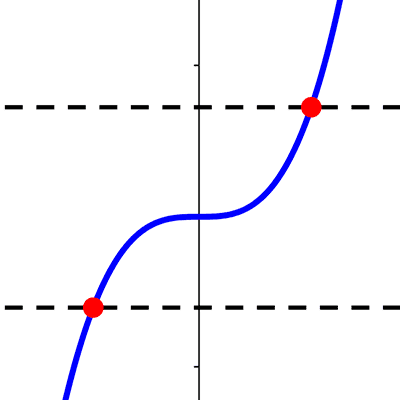
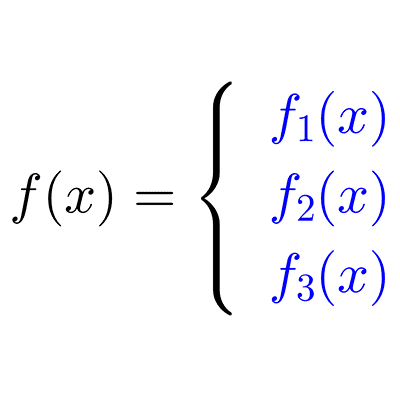


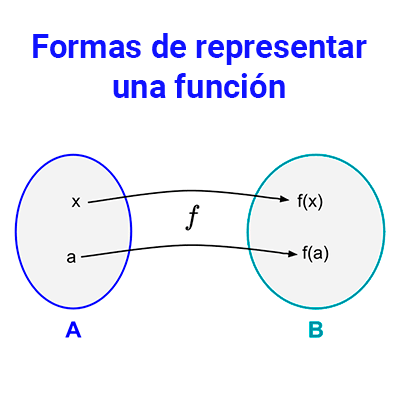





Tipos de funciones
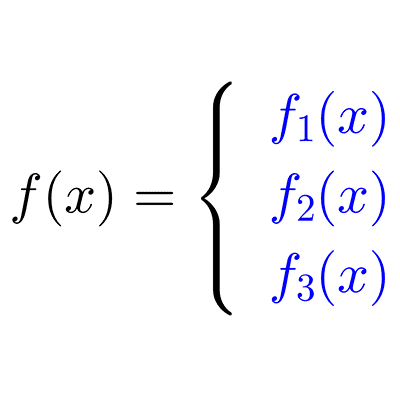
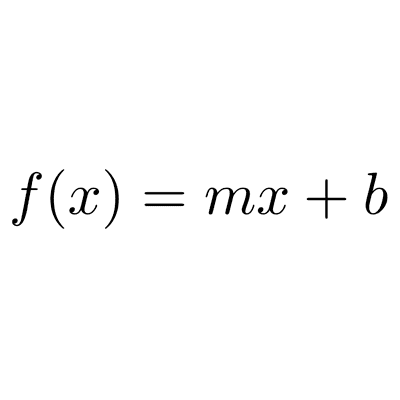
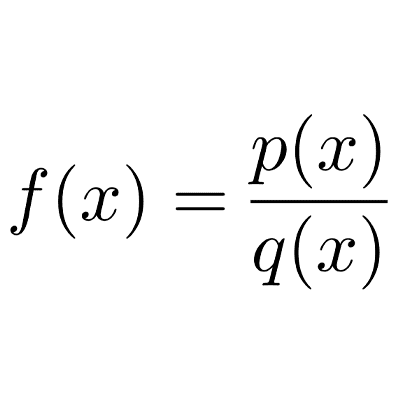
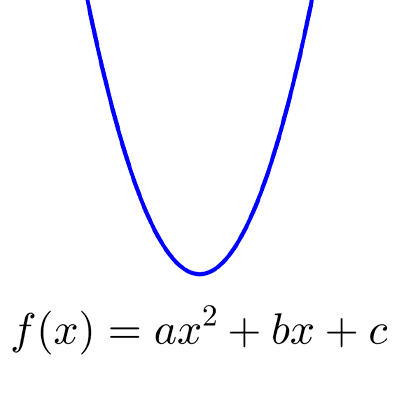
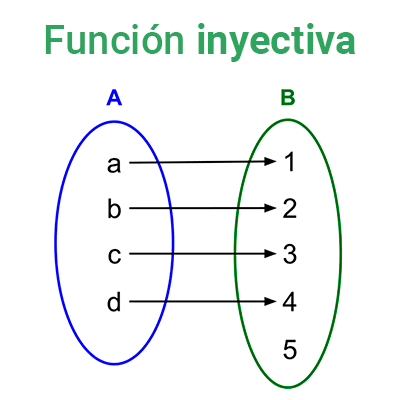
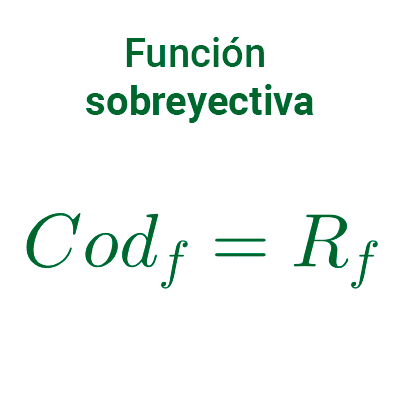
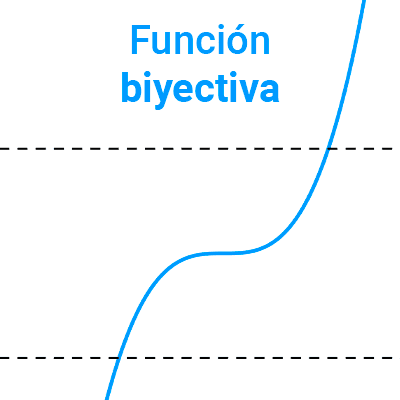
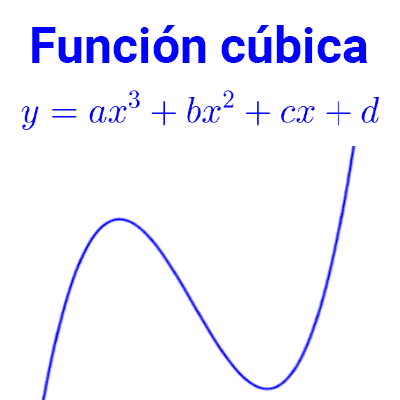



Función cuadrática
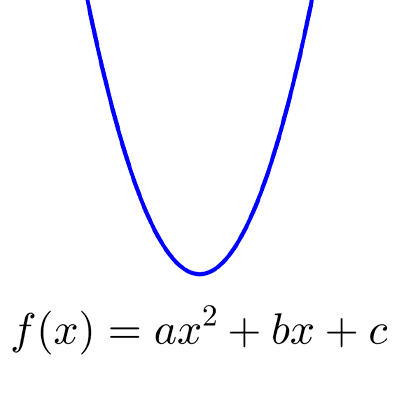








Función lineal
Operaciones con funciones
Límites
El límite de una función es un concepto fundamental en matemáticas que describe el comportamiento de la función en torno a un punto específico. Proporciona información crucial sobre la tendencia de la función en situaciones cercanas a ese punto, permitiendo analizar su comportamiento y propiedades, como continuidad, discontinuidades o valores extremos.




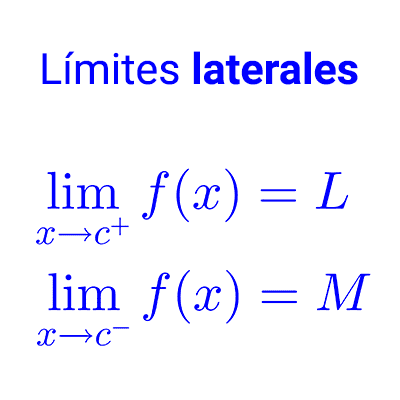
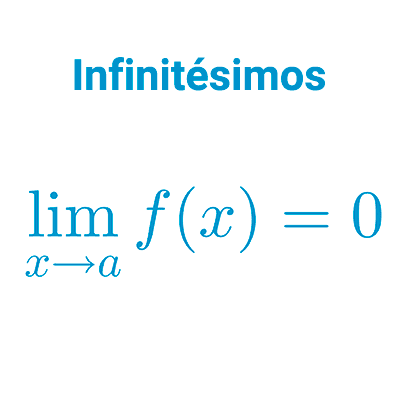

Límites de funciones algebraicas



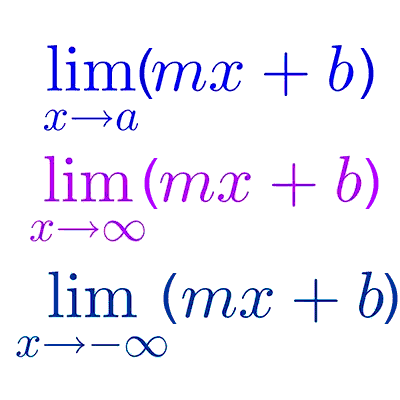

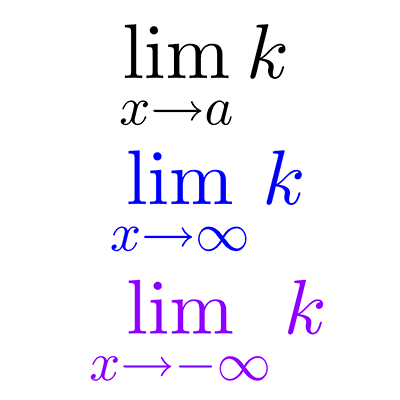

Límites de funciones trascendentes







Lógica matemática
La lógica matemática es una disciplina que se centra en el estudio y la formalización del razonamiento y el pensamiento utilizando un conjunto específico de reglas y símbolos. Su principal objetivo es proporcionar un marco riguroso y preciso para expresar ideas, argumentos y relaciones en el ámbito de las matemáticas.
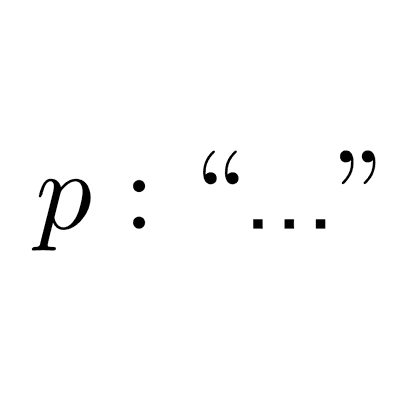
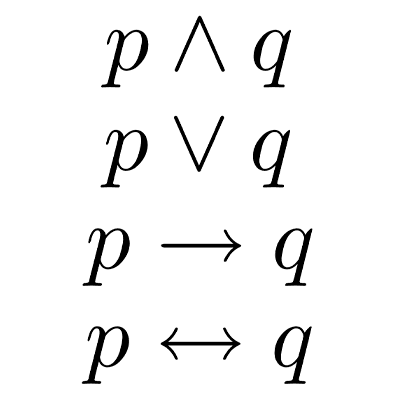
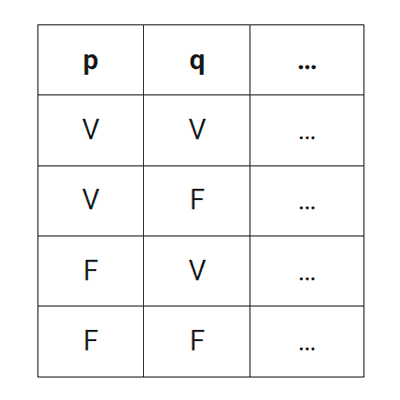

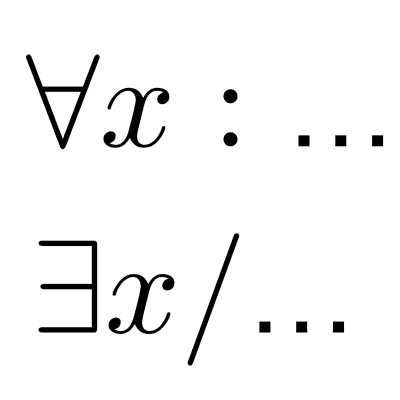
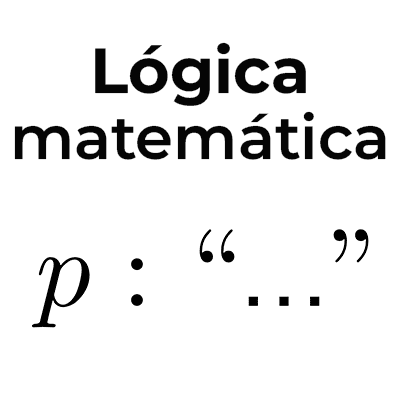







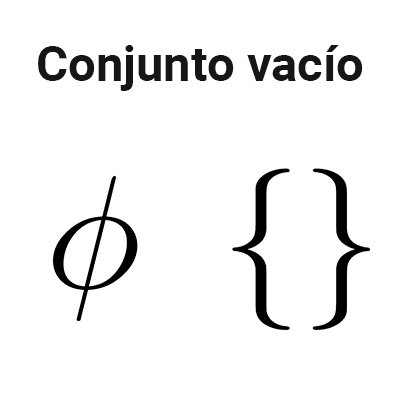
Teoría de conjuntos
La teoría de conjuntos es una rama de la matemática que estudia los conjuntos y las relaciones y operaciones entre ellos.
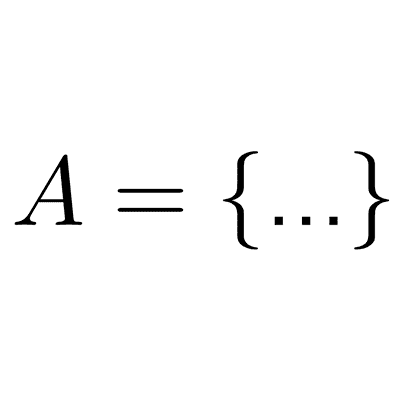
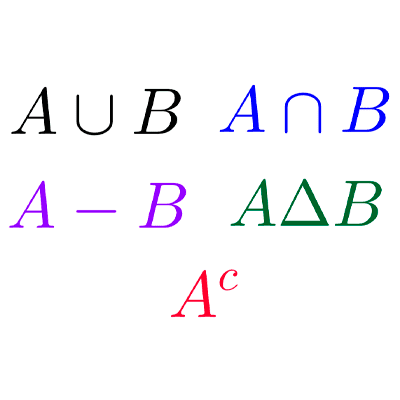
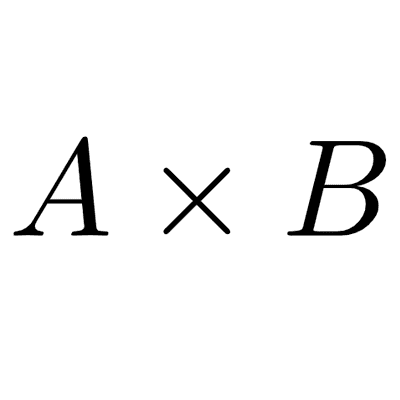
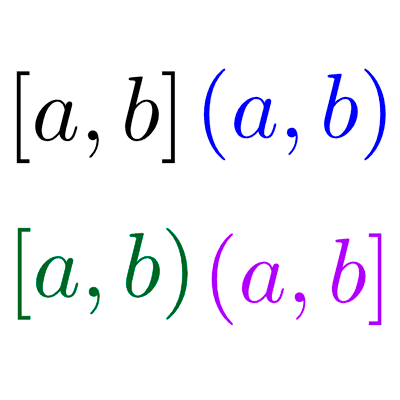

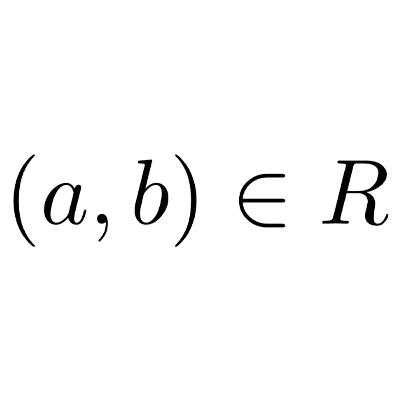








Logaritmos
Un logaritmo es el exponente al que se eleva una base para obtener un determinado número.
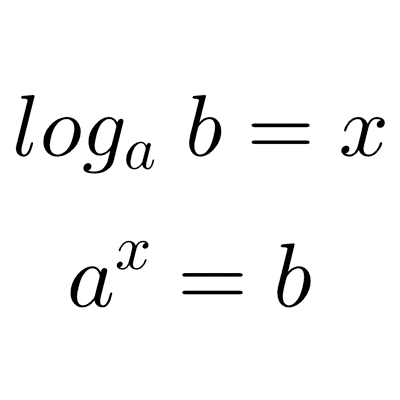
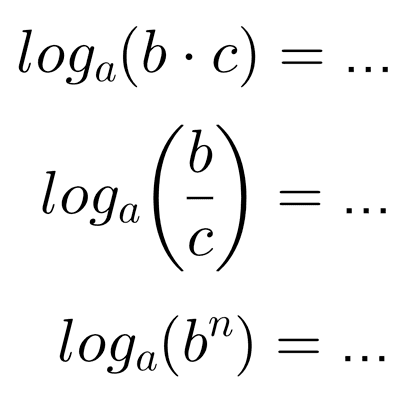



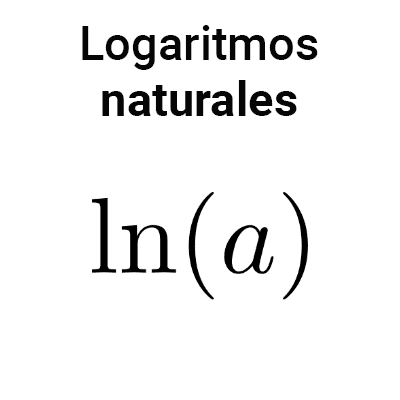



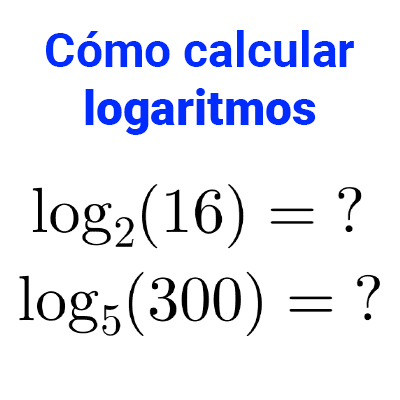






Radicales
Los radicales son números que representan raíces, como la raíz cuadrada o cúbica de un valor. Sirven para expresar cantidades que no son racionales y nos ayudan a calcular medidas precisas, resolver ecuaciones y trabajar con números que no pueden expresarse como números racionales.
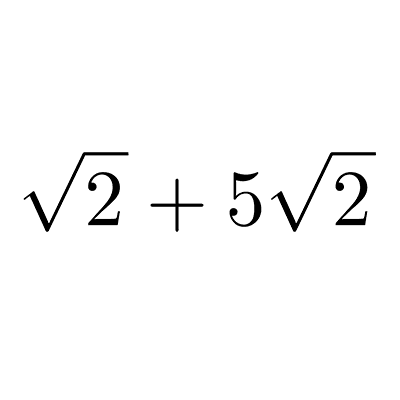

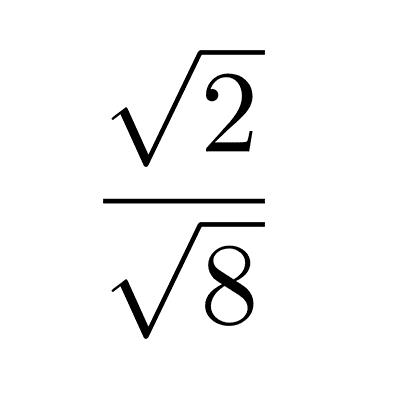
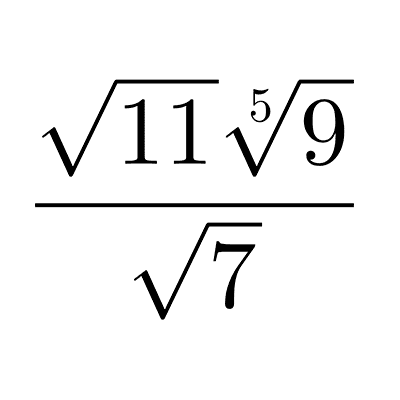
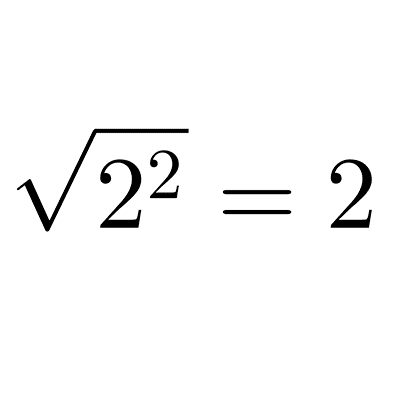
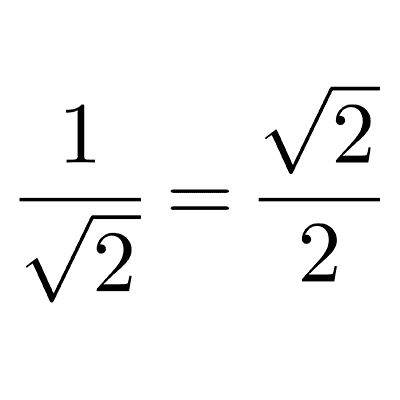
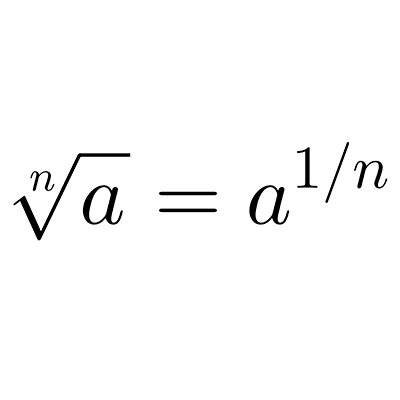
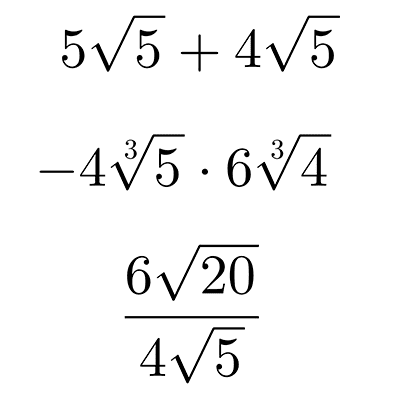


Conjuntos numéricos
Los conjuntos numéricos son una forma de clasificar los distintos tipos de números según sus propiedades y características.