Rango de una función

0 - Votos: 0

En este artículo explicamos qué es el rango de una función, cómo se diferencia del dominio y el codominio y ejemplos de rangos de funciones conocidas.

Índice

¿Qué es el rango?

El rango de una función es el conjunto de todos los valores que puede tomar la variable dependiente, es decir, es el conjunto de los valores de salida que se obtienen al aplicar la función a los elementos del dominio. El rango de una función f se simboliza como R_f, R(f) o Ran_f. Otras formas de llamar al rango son: conjunto imagen, recorrido, ámbito o contradominio.

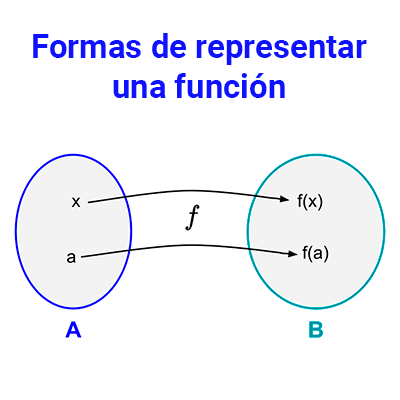
Es importante recordar que una función es una regla que asigna a todo elemento de un conjunto A un único elemento de un conjunto B. El conjunto A es llamado dominio, B es llamado codominio, el rango es entonces un subconjunto de B.

Para las funciones reales, el rango siempre es un subconjunto de números reales. Si f es una función real con dominio D_f, entonces su rango se define como:

*R_f=\{y∈\mathbb{R}~|~y=f(x)~∧~x∈D_f\}*

Diagrama del dominio, codominio y rango de una función. Puede verse que, en este caso, el rango es parte del codominio pero no igual a este.

Los rangos de funciones reales suelen expresarse como intervalos, uniones de intervalos o restas de conjuntos. Los intervalos pueden ser abiertos, cerrados, semiabiertos, finitos o infinitos.

La diferencia entre codominio y rango es que el rango es un subconjunto del codominio, y puede ser más pequeño que este. Pensemos en un salón de clases con 20 alumnos y 25 pupitres; a cada alumno le corresponde un solo pupitre. Tenemos entonces una relación funcional y quedarán ocupados 20 de los 25 pupitres. El conjunto de alumnos es el dominio, el conjunto total de pupitres (25) es el codominio, mientras que el rango son solo los pupitres ocupados (20).

Cuando buscamos determinar el dominio de una función, nos interesan los valores que puede tomar la variable independiente x, en cambio, determinar el rango consiste en encontrar los valores que puede tomar la variable dependiente y=f(x). Si disponemos de una gráfica, el rango de la función puede leerse proyectando la gráfica sobre el eje vertical (eje y).

Gráfica del rango de una función — El rango de una función puede obtenerse de la proyección de la gráfica sobre el eje y.

Ejemplos

A continuación, desarrollamos algunos ejemplos de obtención del rango a partir de las ecuaciones.

Ejemplo 1

La función lineal *y=2x+1* tiene como dominio y rango al conjunto de los números reales, pues no existen restricciones sobre valores que pueden tomar x o y.

Rango de una función lineal — Gráfica de la función lineal. La variable dependiente f(x) puede tomar cualquier valor real.

Ejemplo 2

La función cuadrática *y=x^2* tiene como dominio al conjunto de los números reales. Ahora, como el cuadrado de un número siempre es un número no negativo, la función no toma valores negativos, esto quiere decir que su rango es *[0, +∞)* en notación de intervalos.

Rango de una función cuadrática — Gráfica de la función cuadrática. Puede verse que la variable dependiente (y) solo toma valores no negativos.

Ejemplo 3

La función irracional *y=\sqrt{x}+4* tiene como dominio al conjunto de valores que hacen que el radicando no sea negativo, es decir, el dominio es *[0,+∞).* Como la raíz cuadrada de un número siempre da por resultado un número no negativo, se tiene que *\sqrt{x}≥0.* Si a ambos lados de esta desigualdad sumamos 4, obtenemos:

*\sqrt{x}+4≥0+4*

*\sqrt{x}+4≥4*

*y≥4*

Entonces, como *y* solo puede tomar valores mayores o iguales a 4, el rango de la función es *[4,+∞).*

Rango de una función radical y=raiz(x)+4 — Gráfica de la función radical. La variable dependiente puede tomar valores mayores o iguales a 4.

Rangos de funciones conocidas

A continuación, veremos los rangos de funciones elementales con las que se trabaja habitualmente.

Funciones constantes

El rango de una función constante es el conjunto que contiene a la constante. Es decir, para la función f(x)=c, donde c es un número real, el rango es R_f={c}.

Ejemplos

El rango de *f(x)=5* es *R_f=\{5\}.*
El rango de *g(x)=-8* es *R_g=\{-8\}.*

Funciones lineales

Las funciones lineales que no son constantes tienen como rango al conjunto de los números reales. Es decir, la función *f(x)=mx+b* donde *m* y *b* son reales y *m\neq 0,* tiene como rango a *R_f=\mathbb{R}.*

Ejemplos

El rango de *f(x)=-6x* es *R_f=\mathbb{R}.*
El rango de *y=20x-3* es *\mathbb{R}.*

Funciones cuadráticas

El rango de una función cuadrática, si el coeficiente principal es positivo, es el conjunto de todos los números mayores o iguales a su valor mínimo. Si el coeficiente principal es negativo, el rango es el conjunto de todos los números menores o iguales a su valor máximo. Es decir, dada la función *f(x)=ax^2+bx+c:*

Si *a* es positivo, *R_f=[k,+∞)*
Si *a* es negativo, *R_f=(-∞,k]*

donde *k=f(h)* y *h=\dfrac{-b}{2a}.* El vértice *V(h,k)* es el valor máximo o mínimo de la función.

Ejemplos

El rango de *y=-2x^2+3x+1* es *(-∞, \frac{17}{8}].*
El rango de *f(x)=x^2+9* es *R_f=[9,+∞).*

Funciones cúbicas

El rango de toda función cúbica es el conjunto de los números reales. Es decir, la función *f(x)=ax^3+bx^2+cx+d* donde *a,b,c,d* son números reales y *a\neq 0* tiene como rango a *R_f=\mathbb{R}.*

Ejemplos

El rango de *f(x)=3x^3-4* es *\mathbb{R}.*
El rango de *y=-x^3+2x^2+3* es *\mathbb{R}.*

Funciones racionales

El rango de una función racional puede ser todo el conjunto de números reales o puede estar restringido dependiendo de la función. En el caso de las funciones homográficas, su rango es el conjunto de todos los reales excepto aquel valor donde hay asíntota horizontal.

Ejemplos

El rango de *y=\dfrac{1}{x}* es *\mathbb{R}-\{0\}.*
El rango de *y=\dfrac{2x+1}{x+3}* es *\mathbb{R}-\{2\}.*

Funciones radicales

El rango de una función radical está restringido por la raíz que se está tomando y el radicando. En algunos casos puede ser el conjunto completo de los números reales y en otros solo un subconjunto de este.

Ejemplos

El rango de *y=\sqrt{x}* es *[0,+∞).*
El rango de *y=\sqrt[3]{2x+1}* es *\mathbb{R}.*

Funciones exponenciales

El rango de una función exponencial con base positiva es siempre el conjunto de todos los números reales positivos. Es decir, el rango de *f(x)=a^x* donde *a>0* es *R_f=(0,+∞).*

Ejemplos

El rango de la función exponencial natural es el conjunto de los reales positivos. Para *y=e^x,* el rango es *(0,+∞).*
El rango de *y=(\frac{1}{2})^x* es *(0,+∞).*
El rango de *y=2^x* es *(0,+∞).*

Funciones logarítmicas

El rango de toda función logarítmica es el conjunto de todos los números reales. Es decir, la función *f(x)=\log_a{x}* donde *a>0* y *a\neq 1* tiene como rango a *R_f=\mathbb{R}.*

Ejemplos

El rango de la función logaritmo natural es el conjunto de los números reales. Si *f(x)=\ln{x},* entonces *R_f=\mathbb{R}.*
El rango de la función logaritmo decimal *y=\log{x}* es *\mathbb{R}.*

Funciones trigonométricas

En la siguiente tabla se muestra el rango de las funciones trigonométricas seno, coseno, tangente, cosecante, secante y cotangente.

Función	Rango
Seno	[-1,1]
Coseno	[-1,1]
Tangente	\mathbb{R}
Cosecante	(−∞,−1]∪[1,+∞)
Secante	(−∞,−1]∪[1,+∞)
Cotangente	\mathbb{R}

Bibliografía

Chorny, F., Casares, P. y Salpeter, C. (2015). Matemática 4. Editorial Estrada.
Edwards, C. y Penney, D. (1997). Cálculo Diferencial e Integral (4ta edición). Pearson Educación.
Effenberger, P. (2016). Matemática III. Kapelusz Editora.
Entre Números III. (2016). Santillana.
Larson, R. y Edwards, B. (2010). Cálculo 1 de una variable (9na edición). McGraw Hill.
Leithold, L. (1998). El Cálculo (7ma edición). Oxford University Press.
Matemática 3 ESO. (2011). Santillana Educación.
Piskunov, N. (1977). Cálculo diferencial e integral (3ra edición). Editorial Mir Moscú.
Rabuffetti, H. (1999). Introducción al Análisis Matemático: Cálculo 1 (15a edición). El Ateneo.
Rojo, A. (1996). Álgebra I (18a edición). El Ateneo.
Sadosky, M. y Guber, R. (1984). Elementos de cálculo diferencial e integral (17a edición). Librería y Editorial Alsina.
Stewart, J. (2012). Cálculo de una variable, trascendentes tempranas (7ma edición). Cengage Learning.
Thomas, G. (2006). Cálculo, una variable (11a edición). Pearson Educación.
Wilches, L., Costa, R., Rincón, M., Acosta, M., Roa, J., Sulvara, J. y Jaime, D. (2013). Matemática 6. Editorial Santillana.
Zill, D. y Wright, W. (2011). Cálculo, trascendentes tempranas (4ta edición). McGraw Hill.