Grafica de una función

0 - Votos: 0

En este artículo explicamos qué es la gráfica de una función, cuáles son sus elementos, para qué sirve hacer un análisis y las gráficas de funciones habituales.

Índice

¿Qué es la gráfica?

La gráfica de una función es el conjunto de puntos del plano cartesiano donde la primera coordenada es un valor del dominio y la segunda su imagen correspondiente. Es decir, la gráfica de una función f es un conjunto de puntos (x, y) donde x está en el dominio de la función y además y=f(x). Simbólicamente:

*G_f=\{(x,y)~|~x∈D_f~~\text{y}~~y=f(x)\}*

Por ejemplo, la gráfica de la función *y=2x+1* es el conjunto de todos los puntos del plano cartesiano *(x, y)* donde se cumple que *y=2x+1* y *x* está en el dominio de la función. El dominio se considera sobre el eje horizontal (eje x o eje de abscisas) y el rango sobre el eje vertical (eje y o eje de ordenadas).

Gráfica de la función lineal y=2x+1 — Gráfica de la función y=2x+1

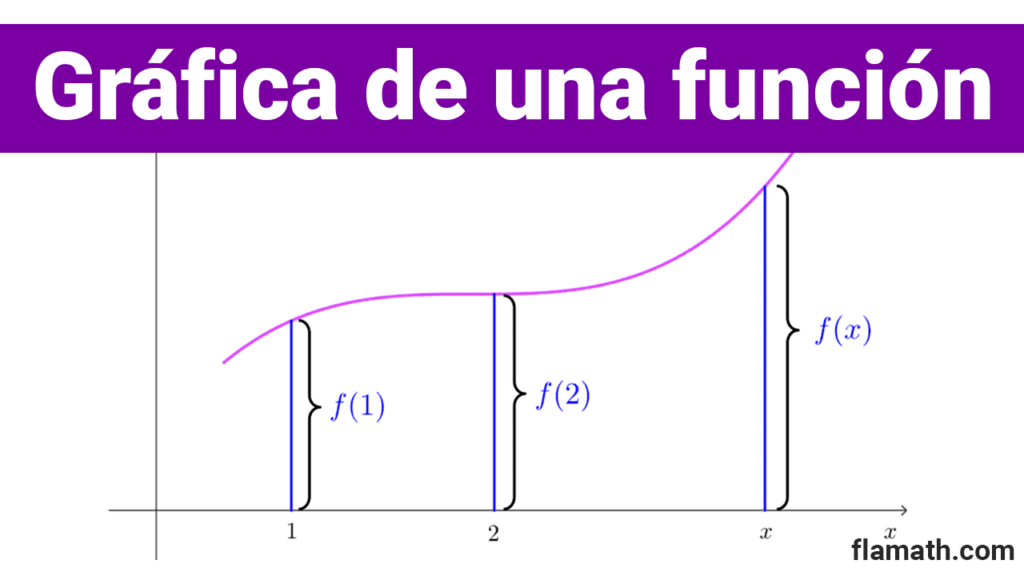
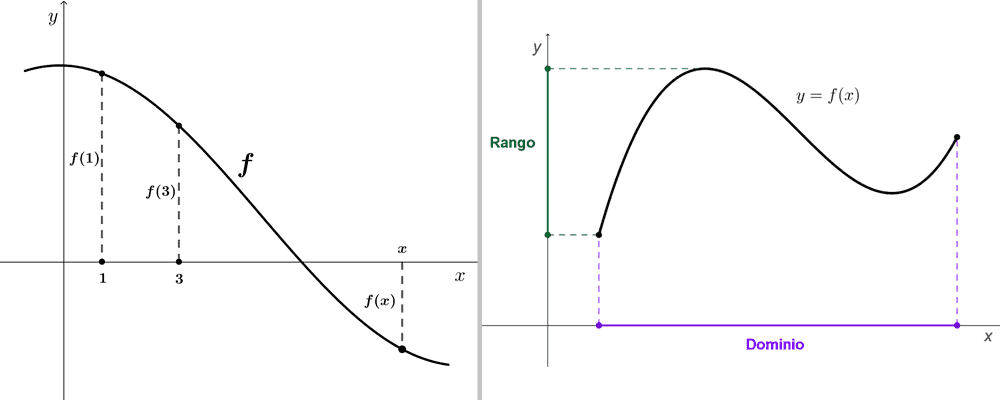
La gráfica es una de las formas de representar una función que permite comprender el comportamiento de la función de manera visual. Si (x, y) es un punto en la gráfica, entonces y=f(x) es la altura de la gráfica en el punto x. Esta puede ser positiva, negativa o cero, lo cual depende del signo de f(x). Además, el dominio y el rango se pueden obtener reflejando la gráfica sobre los ejes cartesianos.

Para qué sirve la gráfica de una función

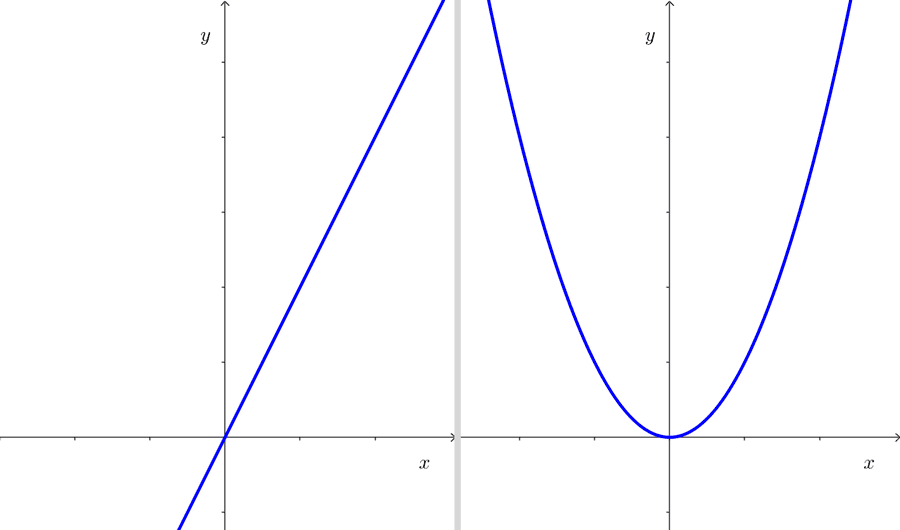
La forma de la gráfica puede variar según la naturaleza de la función. Por ejemplo, una función lineal producirá una línea recta en el plano cartesiano (como en el primer ejemplo), mientras que una función cuadrática generará una curva llamada parábola. Otras funciones producen diferentes curvas.

Gráficas de una función lineal y una función cuadrática — Gráficas de una función lineal (izquierda) y una función cuadrática (derecha)

En la mayoría de funciones reales no es posible representar todos puntos (x, y), porque son infinitos. Para hacer gráficas es común representar algunos puntos significativos y trazar el resto de la gráfica teniendo en cuenta las propiedades de la función.

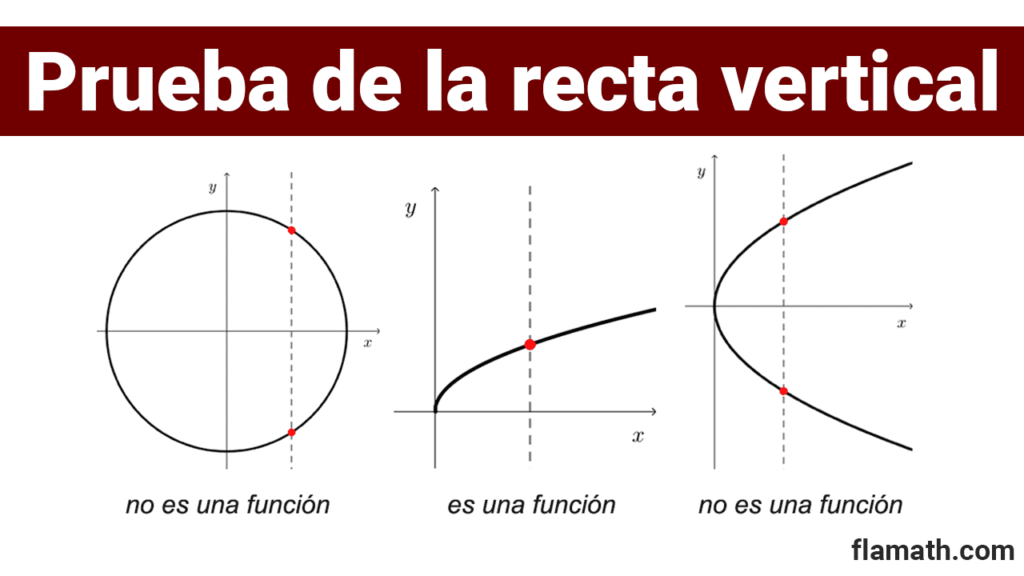
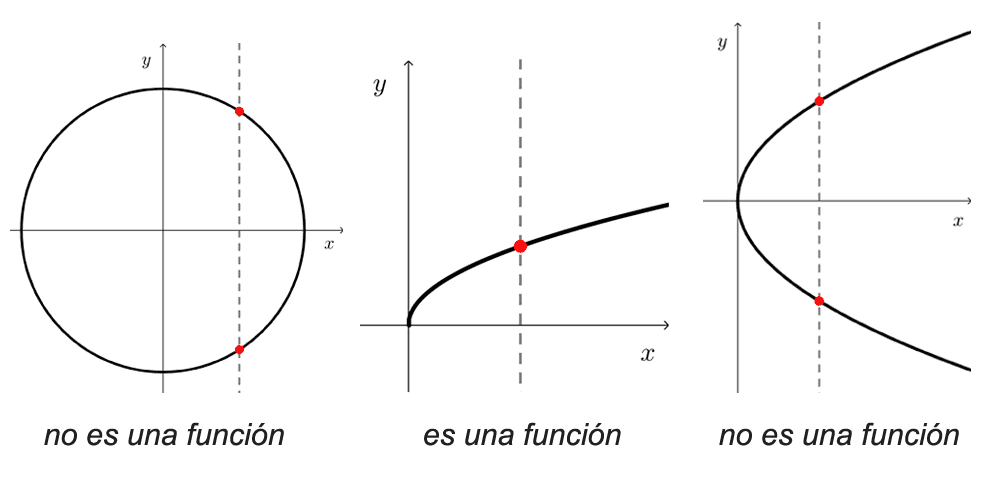
No todos los trazos en un plano cartesiano pueden corresponder a una función. Las gráficas de funciones tienen la propiedad de que una recta vertical puede cortarlas a lo sumo en un punto, pues en caso contrario significa que un mismo número tiene más de una imagen, no cumpliendo con la definición de función.

Esta observación proporciona un criterio visual adecuado para diferenciar la gráfica de una función de otras curvas. Habitualmente se la llama prueba de la recta vertical, y nos dice que un trazo en el plano es gráfico de una función si y sólo si ninguna recta vertical la interseca más de una vez.

Prueba de la recta vertical para determinar si una curva es gráfica de una función o no — Prueba de la recta vertical

Elementos de la gráfica

Podemos destacar como elementos de una gráfica a los siguientes:

Ejes cartesianos: el eje horizontal (eje x) donde se ubica al dominio de la función y el eje vertical (eje y) donde se ubica al rango. El punto donde se cortan los ejes se llama origen de coordenadas.
Puntos: cada punto en la gráfica es un par ordenado *(x, y)* donde *y=f(x).* El valor de x se llama abscisa del punto y el valor de y se llama ordenada.
Curva: la mayoría de funciones con las que se trabajan describen una curva, la cual pasa por todos los puntos de la función.
Intersecciones con los ejes: la gráfica de una función puede cortar tanto al eje x, cuando *y=0,* o al eje y, cuando *x=0.* Las intersecciones con el eje x reciben el nombre de ceros o raíces y pueden ser infinitas. A su vez, la intersección con el eje y, si existe, es única.

Intersecciones de una función con el eje x

Intersección de una función con el eje y

Análisis de gráficas

Las características importantes de una función pueden ser identificadas a partir del análisis de su gráfica. Algunas de las propiedades que se pueden encontrar son:

Signo de la función: una función puede tener intervalos donde es positiva y otros donde es negativa. Si la gráfica se encuentra por encima del eje x, la función es positiva. Si la gráfica se encuentra por debajo del eje x, la función es negativa. Si en un punto la gráfica corta al eje x, este punto es un cero o raíz, y puede cambiar el signo de la función si esta logra traspasar el eje.
Simetría: algunas funciones pueden ser simétricas con respecto al eje y, estas reciben el nombre de funciones pares; o pueden ser simétricas respecto al origen de coordenadas, y reciben el nombre de funciones impares.
Intervalos de crecimiento y decrecimiento: estos son intervalos en los que la función está aumentando o disminuyendo, respectivamente. Se pueden identificar observando la dirección de la curva de la función en esos intervalos.
Máximos y mínimos: son los puntos más altos (máximos) y más bajos (mínimos) en la gráfica de una función. Pueden ser relativos o absolutos, dependiendo de si son los puntos más altos o más bajos en un intervalo específico o en todo el dominio de la función.
Comportamientos asintóticos: algunas funciones pueden tender a acercarse a rectas a medida que la variable independiente se aproxima a ciertos valores. Estas rectas reciben el nombre de asíntotas y pueden ser horizontales, verticales u oblicuas. El comportamiento asintótico es habitual en funciones racionales, aunque existen más funciones que lo tienen.
Concavidad de la función: se refiere a la orientación de la gráfica de la función en un intervalo determinado. Puede ser cóncava hacia arriba (con forma de U) o cóncava hacia abajo (con forma de ∩).
Puntos de inflexión: son los puntos donde la concavidad de la curva de la función cambia. En estos puntos, la función puede cambiar de ser cóncava hacia arriba a cóncava hacia abajo, o viceversa.

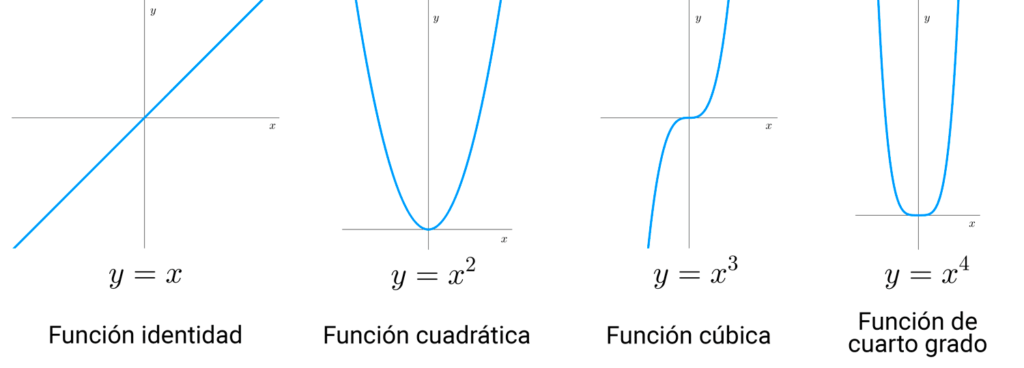
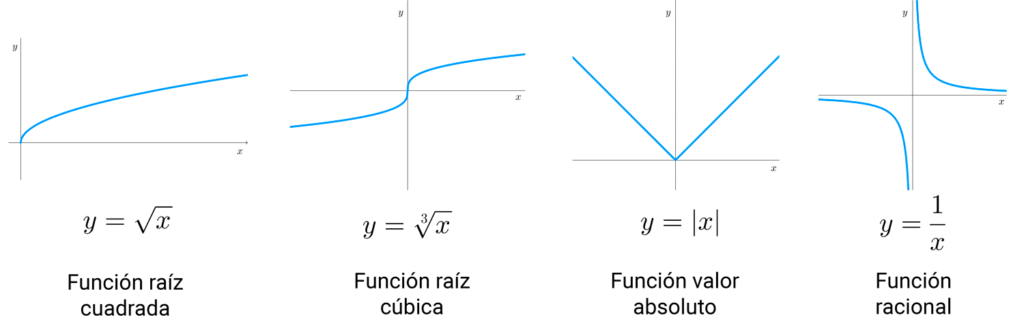
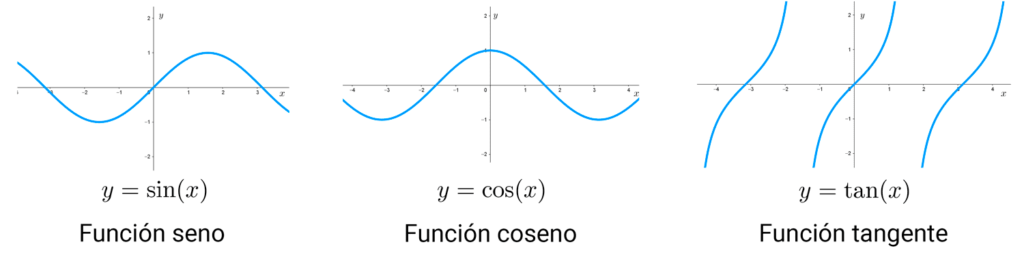
Gráficas de funciones conocidas

En las siguientes imágenes se muestran los gráficos de funciones habituales que es importante conocer.

Gráficas de la función identidad y=x, función cuadrática y=x^2, función cúbica y=x^3 y función de cuarto grado y=x^4

Gráficas de la función raíz cuadrada, raíz cúbica, valor absoluto y función racional 1/x

Gráficas de funciones trigonométricas seno, coseno y tangente

Gráficas de funciones trigonométricas inversas arcoseno, arcocoseno y arcontangente

Bibliografía

Chorny, F., Casares, P. y Salpeter, C. (2015). Matemática 4. Editorial Estrada.
Edwards, C. y Penney, D. (1997). Cálculo Diferencial e Integral (4ta edición). Pearson Educación.
Effenberger, P. (2016). Matemática III. Kapelusz Editora.
Entre Números III. (2016). Santillana.
Larson, R. y Edwards, B. (2010). Cálculo 1 de una variable (9na edición). McGraw Hill.
Leithold, L. (1998). El Cálculo (7ma edición). Oxford University Press.
Matemática 3 ESO. (2011). Santillana Educación.
Piskunov, N. (1977). Cálculo diferencial e integral (3ra edición). Editorial Mir Moscú.
Rabuffetti, H. (1999). Introducción al Análisis Matemático: Cálculo 1 (15a edición). El Ateneo.
Rojo, A. (1996). Álgebra I (18a edición). El Ateneo.
Sadosky, M. y Guber, R. (1984). Elementos de cálculo diferencial e integral (17a edición). Librería y Editorial Alsina.
Stewart, J. (2012). Cálculo de una variable, trascendentes tempranas (7ma edición). Cengage Learning.
Thomas, G. (2006). Cálculo, una variable (11a edición). Pearson Educación.
Wilches, L., Costa, R., Rincón, M., Acosta, M., Roa, J., Sulvara, J. y Jaime, D. (2013). Matemática 6. Editorial Santillana.
Zill, D. y Wright, W. (2011). Cálculo, trascendentes tempranas (4ta edición). McGraw Hill.