Límites laterales
En este artículo desarrollamos los límites laterales por izquierda y por derecha. Veremos qué son y ejemplos de cómo se calculan, su importancia para el cálculo y las propiedades que cumplen.
Índice
Concepto y definición intuitiva
Sabemos que para que exista el límite de una función en un punto, esta tiene que estar definida a ambos lados del punto y las imágenes deben aproximarse a un número fijo cuando la variable independiente se aproxima al punto de interés.
Si la función carece de límite en un punto, podría tener un límite lateral, esto es, un límite si la aproximación es solo por un lado. Si la aproximación se da por la derecha, el límite es un límite por la derecha. Si es por la izquierda, es un límite por la izquierda. A los límites ordinarios se les suele llamar límites bilaterales.
Límite por la derecha: si f es una función definida en un intervalo abierto (c, b) con c<b y f(x) se aproxima a L cuando x tiende a c dentro de ese intervalo, entonces f tiene límite por la derecha y es igual a L en c. En símbolos:
$$\lim_{x\to c^+} f(x)=L$$
El símbolo *x\to c^+* significa que solo consideramos valores de x mayores a c (x>c).
Límite por la izquierda: si f es una función definida en un intervalo abierto (a, c) con a<c, y f(x) se aproxima a M cuando x tiende a c dentro de ese intervalo, entonces f tiene límite por la izquierda igual a M en c. En símbolos:
$$\lim_{x\to c^-} f(x)=M$$
El símbolo *x\to c^-* significa que solo consideramos valores de x menores que c (x<c).
Ejemplos de límites laterales
Ejemplo 1: límites laterales a partir de una gráfica.
La gráfica de una función f se muestra a continuación. La usaremos para hallar los siguientes límites (si existen):
- *\lim_{x\to 1^-} f(x)*
- *\lim_{x\to 1^+} f(x)*
- *\lim_{x\to 1} f(x)*
- *\lim_{x\to 2^-} f(x)*
- *\lim_{x\to 2^+} f(x)*
- *\lim_{x\to 2} f(x)*
Observando la gráfica, podemos llegar a las siguientes conclusiones:
- Cuando x tiende a 1 por la izquierda, f(x) tiende a 1, por tanto: *\lim_{x\to 1^-} f(x)=1*
- Cuando x se acerca a 1 por la derecha, f(x) se acerca a 3, por tanto, *\lim_{x\to 1^+} f(x)=3*
- Cuando x se acerca a 1 tanto por izquierda como por derecha, f(x) no se acerca a un mismo valor fijo, por tanto *\lim_{x\to 1} f(x)* no existe.
- Cuando x tiende a 2 por la izquierda, f(x) tiende a 3, por tanto *\lim_{x\to 2^-} f(x)=3*
- Cuando *x\to 2* por la derecha, *f(x)\to 3,* por tanto *\lim_{x\to 2^+} f(x)=3*
- Cuando x se acerca a 2, f(x) se acerca a 3 tanto por izquierda como por derecha, por tanto *\lim_{x\to 2} f(x)=3*
Ejemplo 2: hallar límites laterales algebraicamente.
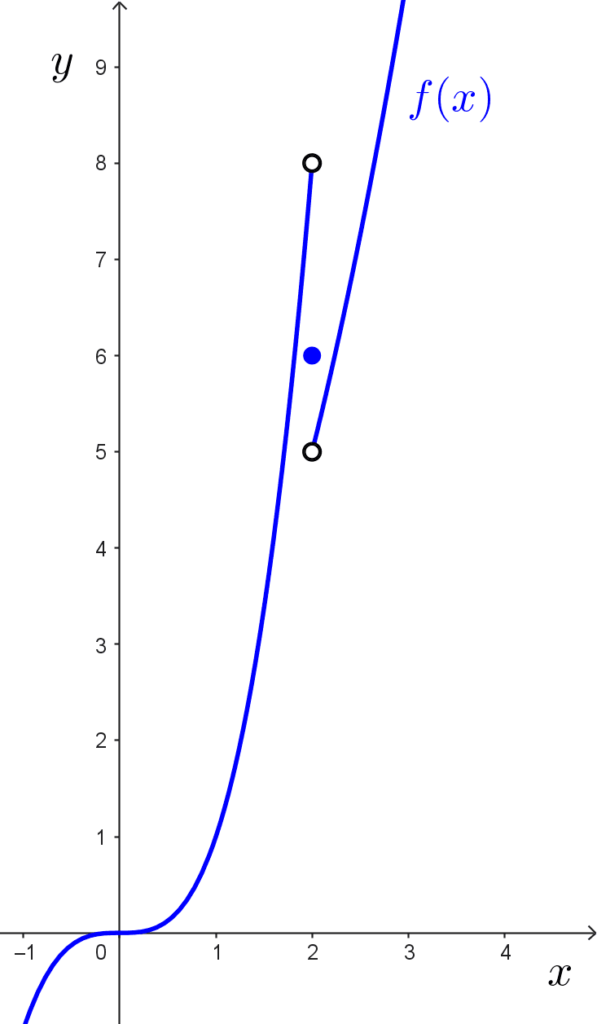
Buscamos hallar los límites laterales *\lim_{x\to 2^-} f(x),* *\lim_{x\to 2^+} f(x)* y el límite ordinario *\lim_{x\to 2} f(x)* si existen, siendo f la siguiente función por partes:
$$f(x)=\begin{cases}x^3~~~\text{si}~x<2 \\ x^2+1~~~\text{si}~x>2 \\ 6~~~\text{si}~x=2 \end{cases}$$
1) Para hallar *\lim_{x\to 2^-} f(x),* debemos tener en cuenta la definición: cuando calculamos un límite por izquierda solo tomamos valores de x menores al del punto de interés. En este caso, debemos tomar valores de x menores a 2, o sea, *x<2.* La fórmula de la función cuando *x<2* es *f(x)=x^3.* Entonces:
$$\lim_{x\to 2^-} f(x)=\lim_{x\to 2^-} x^3=2^3=8$$
2) Para encontrar *\lim_{x\to 2^+} f(x)* tomamos en cuenta sólo valores de x mayores a 2, o sea, *x>2.* Cuando *x>2,* la función es *f(x)=x^2+1,* entonces:
$$\lim_{x\to 2^+} f(x)=\lim_{x\to 2^+} (x^2+1)=2^2+1=5$$
3) Cuando *x\to 2* tanto por izquierda como por derecha, los valores de *f(x)* tienden a números distintos, como pudimos ver con los límites laterales. Como *f(x)* no se acerca a un mismo número fijo, el límite en 2 no existe.
*\lim_{x\to 2} f(x)* no existe.
Ejemplo 3: puntos en donde sólo existen límites laterales.
Dijimos al comienzo que si no existe el límite ordinario en un punto aún pueden existir límites laterales, lo veremos en este caso. A continuación tenemos la gráfica de la función *f(x)=\sqrt{4-x^2}*, la cual es una semicircunferencia.
Tenemos:
$$\lim_{x\to -2^+} \sqrt{4-x^2}=0$$
$$\lim_{x\to 2^-} \sqrt{4-x^2}=0$$
La función no tiene límite por la izquierda en *x=-2* ni límite por la derecha en *x=2.* Por tanto, tampoco tiene límites ordinarios en *-2* y *2.*
Importancia de los límites laterales
Los límites laterales tienen gran importancia porque dan pie a la condición para que exista el límite de una función en un punto.
Una función f tiene límite cuando x tiende a c si y sólo si ahí existen límites por la derecha y por la izquierda, y además si estos límites laterales son iguales:
*\lim_{x\to c} f(x)=L~* si y solo si *~\lim_{x\to c^-} f(x)=\lim_{x\to c^+} f(x)=L*
Ejemplo 1: los límites laterales no coinciden
Sea la función por partes H(x):
*H(x)=\begin{cases}0, x<0 \\ 1, x>0 \end{cases}*
Cuando x tiende a 0 por la izquierda, H(x) tiende a cero, o sea, *\lim_{x\to 0^-} H(x)=0.* Si x se acerca por la derecha, H(x) se aproxima a 1, o sea, *\lim_{x\to 0^+} H(x)=1.* Como los límites laterales son diferentes, H(x) no tiende a un mismo número fijo cuando *x\to 0,* por tanto el límite ordinario *\lim_{x\to 0} H(x)* no existe.
Ejemplo 2: límites laterales que coinciden
Algunos límites se pueden calcular mejor si primero encontramos los límites por la izquierda y por la derecha. Buscamos demostrar que *\lim_{x\to 0} |x|=0*
Sabemos que la función valor absoluto se puede descomponer por partes así:
*|x|=\begin{cases}x~~~\text{si}~x≥0 \\ -x~~~\text{si}~x<0\end{cases}*
Como *|x|=x* para *x>0,* tenemos que *\lim_{x\to 0^+} |x|=\lim_{x\to 0^+} x=0*
Para *x<0,* tenemos que *|x|=-x* y así:
*\lim_{x\to 0^-} |x|=\lim_{x\to 0^-} (-x)=0*
Como los límites laterales son iguales, hemos demostrado que *\lim_{x\to 0} |x|=0*
Propiedades de los límites laterales
Los límites laterales cumplen las mismas propiedades de los límites ordinarios.
Sea k es una constante y supongamos que existen los siguientes límites laterales:
*\lim_{x\to a^+} f(x)* *\lim_{x\to a^+} g(x)*
*\lim_{x\to a^-} f(x)* *\lim_{x\to a^-} g(x)*
entonces se cumplen las siguientes propiedades.
Ley de la suma:
$$\lim_{x\to a^+} [f(x)+g(x)]=\lim_{x\to a^+} f(x) + \lim_{x\to a^+} g(x)$$
$$\lim_{x\to a^-} [f(x)+g(x)]=\lim_{x\to a^-} f(x) + \lim_{x\to a^-} g(x)$$
Ley de la diferencia:
$$\lim_{x\to a^+} [f(x)-g(x)]=\lim_{x\to a^+} f(x) - \lim_{x\to a^+} g(x)$$
$$\lim_{x\to a^-} [f(x)-g(x)]=\lim_{x\to a^-} f(x) - \lim_{x\to a^-} g(x)$$
Ley del múltiplo constante:
$$\lim_{x\to a^+} [k\cdot f(x)]=k\cdot \lim_{x\to a^+} f(x)$$
$$\lim_{x\to a^-} [k\cdot f(x)]=k\cdot \lim_{x\to a^-} f(x)$$
Ley del producto:
$$\lim_{x\to a^+} [f(x)\cdot g(x)]=\lim_{x\to a^+} f(x)\cdot \lim_{x\to a^+} g(x)$$
$$\lim_{x\to a^-} [f(x)\cdot g(x)]=\lim_{x\to a^-} f(x)\cdot \lim_{x\to a^-} g(x)$$
Ley del cociente:
$$\lim_{x\to a^+} \dfrac{f(x)}{g(x)}=\dfrac{\lim_{x\to a^+} f(x)}{\lim_{x\to a^+} g(x)}~~~(\text{siempre que } \lim_{x\to a^+} g(x)≠0)$$
$$\lim_{x\to a^-} \dfrac{f(x)}{g(x)}=\dfrac{\lim_{x\to a^-} f(x)}{\lim_{x\to a^-} g(x)}~~~(\text{siempre que } \lim_{x\to a^-} g(x)≠0)$$
Ley de la potencia:
$$\lim_{x\to a^+} [f(x)]^n=[\lim_{x\to a^+} f(x)]^n$$
$$\lim_{x\to a^-} [f(x)]^n=[\lim_{x\to a^-} f(x)]^n$$
n es un entero positivo.
Ley de la raíz:
$$\lim_{x\to a^+} \sqrt[n]{f(x)}=\sqrt[n]{\lim_{x\to a^+} f(x)}$$
$$\lim_{x\to a^-} \sqrt[n]{f(x)}=\sqrt[n]{\lim_{x\to a^-} f(x)}$$
n es un entero positivo. Si n es par, supongamos que *\lim_{x\to a^+} f(x)>0* y *\lim_{x\to a^-} f(x)>0*
Subir
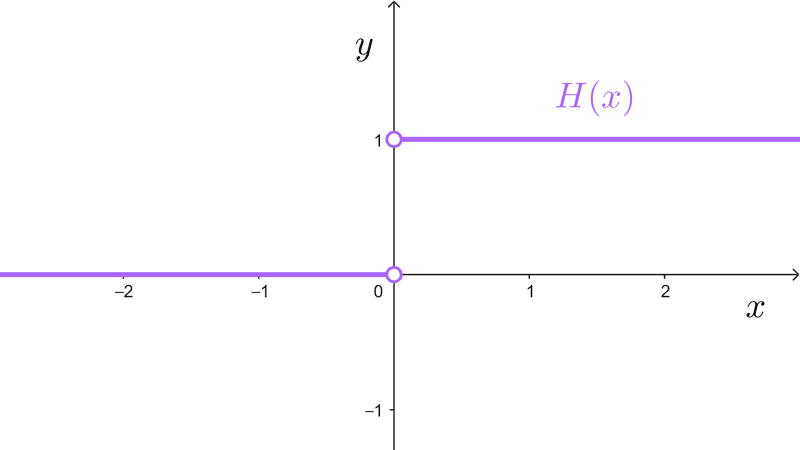
Deja una respuesta