Función cuadrática
En este artículo explicamos qué es una función cuadrática y cuáles son sus elementos y propiedades. Además, veremos ejemplos y las diferentes formas en la que se puede escribir su ecuación.
Índice
¿Qué es una función cuadrática?
Una función cuadrática es una función polinómica de segundo grado, es decir, de la forma f(x)=ax2+bx+c donde a, b y c son números reales fijos y a ≠ 0.
Algunos ejemplos de funciones cuadráticas son:
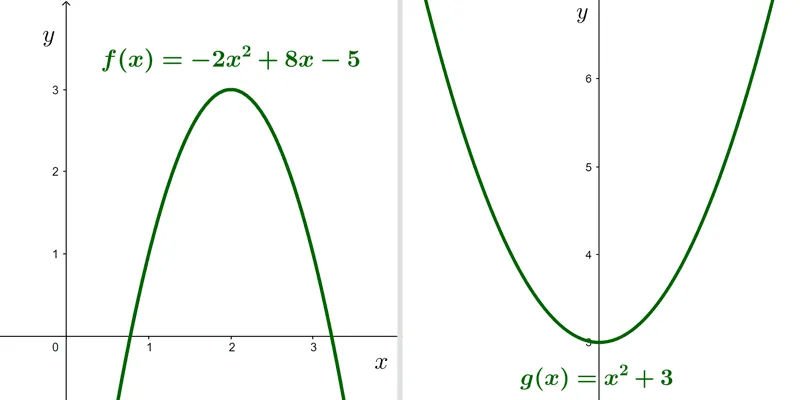
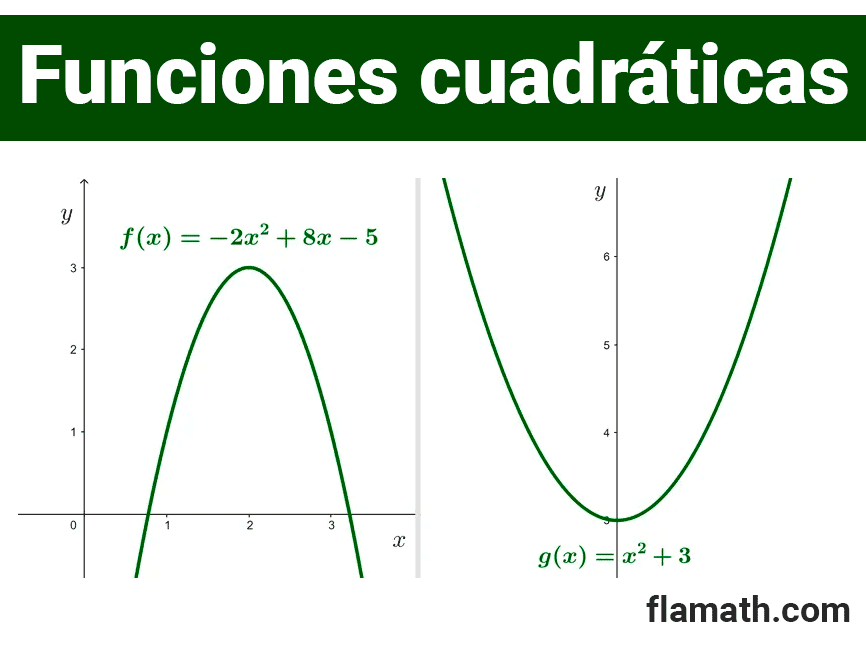
- f(x)= -2x2 + 8x - 5
- g(x)= x2 + 3
- h(x)= 6x2
- y= 2x - x2
- y= -1 + x2 + 2x
Una función como k(x) = 2x - 9, no es cuadrática, puesto que no tiene término cuadrático. Tampoco lo es m(x) = x3+3x2-8x+5, porque, aunque tiene posee término cuadrático, no es un polinomio de segundo grado, sino de tercero.
Elementos y propiedades
Las funciones cuadráticas tienen una serie de partes o elementos que determinan sus características y nos permiten estudiarla, estos elementos son:
- Coeficientes.
- Dominio y rango.
- Gráfica.
- Vértice.
- Eje de simetría.
- Raíces.
- Intersección con el eje y.
Coeficientes
Los coeficientes de una función cuadrática son los números reales a, b y c que aparecen en la fórmula general de la función, f(x) = ax2 + bx + c. Cada una de estas partes tiene un nombre especial:
- a es el coeficiente del término cuadrático o coeficiente principal. Nunca puede ser cero.
- b es el coeficiente del término lineal. Puede ser cero.
- c es el término independiente o constante. Puede ser cero.
De forma similar, el término ax2 se llama término cuadrático o principal, el término bx se denomina término lineal, y c se llama término independiente.
Dominio y rango
El dominio de una función es el conjunto de todos los valores que puede tomar la variable independiente (generalmente denotada con x). El rango de una función es el conjunto de todos los valores que puede tomar la variable dependiente (generalmente denotada como y o f(x)).
El dominio de una función cuadrática es siempre el conjunto de los números reales, es decir, *\mathbb{R}.* El rango, en cambio, depende de los coeficientes, ya que estos determinarán los valores que tomará la función.
Gráfica
La representación gráfica de una función cuadrática es una curva llamada parábola, la cual es simétrica respecto a una recta vertical que llamamos eje de simetría.
Cuando la parábola se abre "hacia arriba", se dice que la función es convexa. Si la parábola se abre "hacia abajo", la función es cóncava. Que sea un caso u otro depende del signo del coeficiente principal, el cual, si es positivo, provocará una parábola hacia arriba; y si es negativo, provocará una parábola hacia abajo.
Dada una función cuadrática f(x) = ax2 + bx + c:
La parábola abre hacia arriba si a>0
La parábola abre hacia abajo si a<0
Vértice
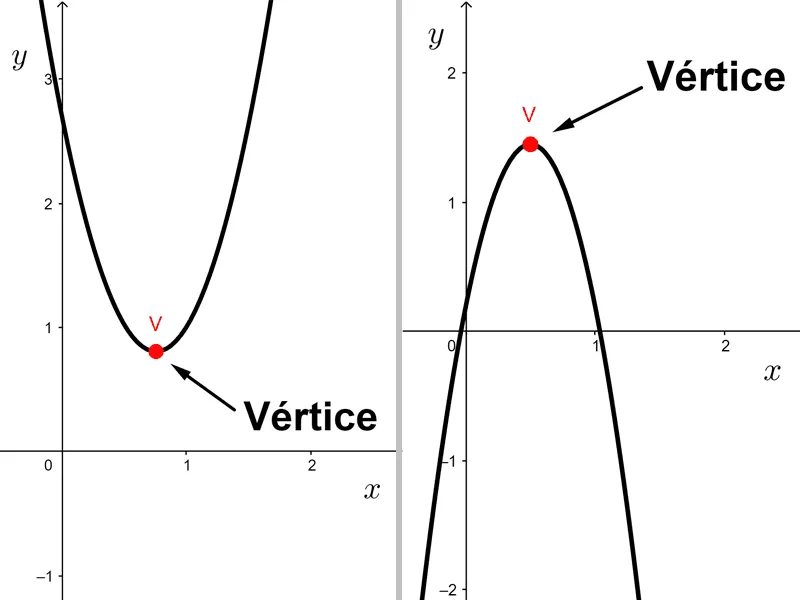
Si la parábola se abre hacia arriba, podemos ver que existe un punto que es más bajo que todos; si abre hacia abajo, hay un punto que está más alto que todos. El punto más bajo o más alto de la parábola se llama vértice. Este punto, por definición, es mínimo o máximo de la función, respectivamente.
El vértice V de la función f(x) = ax2 + bx + c tiene coordenadas (h, k) donde:
*h=\dfrac{-b}{2a}*
*k=f(h)*
Si a>0, el vértice es un mínimo de la función. Si a<0, el vértice es un máximo.
Eje de simetría
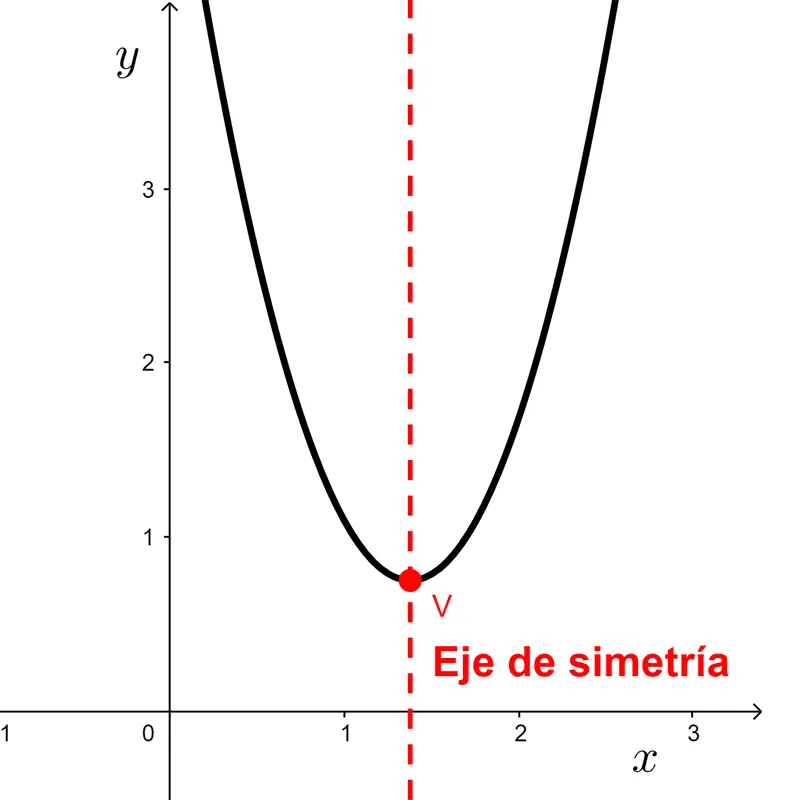
Decíamos anteriormente que la parábola es simétrica respecto a una recta vertical que llamamos eje de simetría (a veces se abrevia como "eje"). Debido a esta simetría es posible encontrar otros puntos de la curva.
El eje de simetría es la recta paralela al eje y que pasa por el vértice y su ecuación es *x=\dfrac{-b}{2a}*
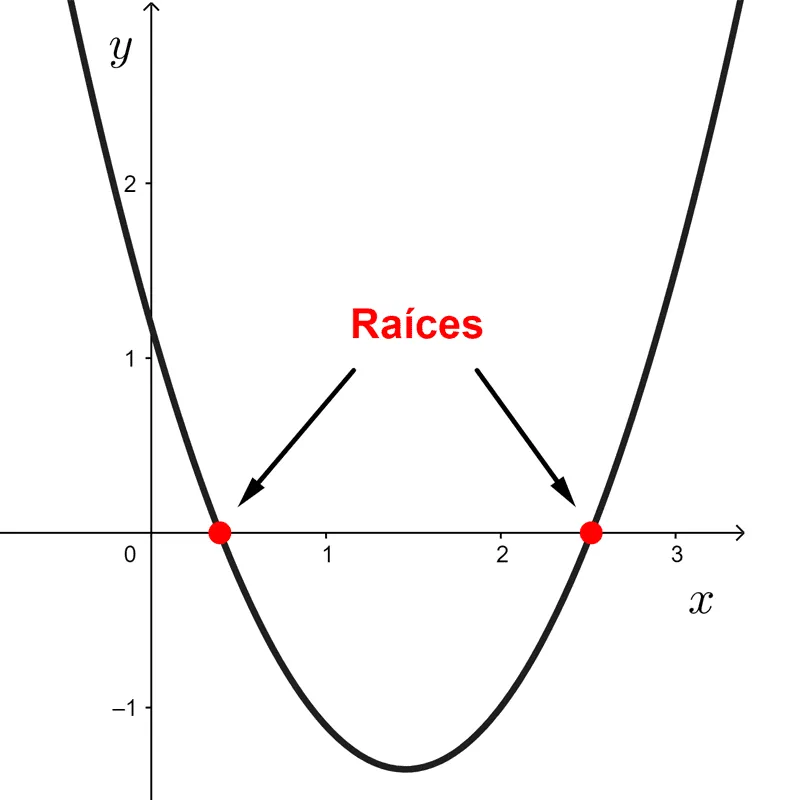
Raíces
Las raíces o ceros de una función son los valores de x donde ella se anula, es decir, f(x) = 0. En estos puntos la gráfica de la función corta al eje x.
Sustituyendo f(x) por 0 en una función cuadrática se obtiene la ecuación ax2 + bx + c = 0. Esta puede ser resuelta mediante la fórmula resolvente para ecuaciones cuadráticas, también llamada fórmula general o de Bhaskara:
*x=\dfrac{-b±\sqrt{b^2-4ac}}{2a}*
Habiendo una raíz cuadrada en esta fórmula, sabemos que solo existe si su radicando es no negativo, siendo en caso contrario un número imaginario. Este radicando recibe el nombre de discriminante, y se lo denota con la letra griega delta mayúscula:
*Δ=b^2-4ac*
La importancia del discriminante radica en que nos dirá si la función cuadrática tiene o no raíces reales. Pueden darse tres casos, los cuales vemos a continuación.
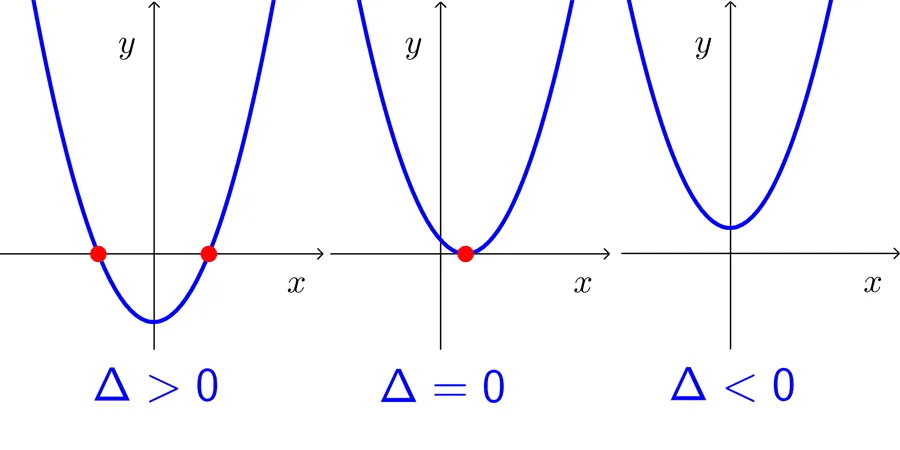
Sea f(x)=ax2+bx+c una función cuadrática y Δ=b2-4ac su discriminante:
- Si el discriminante es positivo, la función tiene dos raíces reales diferentes. Es decir, la gráfica cruza el eje x en dos puntos.
- Si el discriminante es cero, la función tiene una raíz real de multiplicidad 2. Es decir, la gráfica toca al eje x en un punto.
- Si el discriminante es negativo, la función no tiene raíces reales. Es decir, la gráfica no cruza ni toca al eje x.
Intersección con el eje y
La intersección de la gráfica de una función con el eje y, si existe, es única y se da cuando x=0. Como el dominio de una función cuadrática son todos los números reales, el cero está en el dominio y su imagen es:
*f(0)=a(0)^2+b(0)+c=c*
Entonces, el corte de la gráfica de una función cuadrática con el eje y se da en el punto (0, c). Algunas veces este punto es llamado ordenada al origen, aunque este nombre está reservado para las funciones lineales.
Ecuaciones de una función cuadrática
Existen tres tipos de funciones cuadráticas que dependen de la forma en que se exprese su ecuación y tienen diferentes utilidades dependiendo de para qué las estemos usando.
Forma polinómica o general
Esta es la forma que venimos trabajando hasta ahora y corresponde a un polinomio de segundo grado:
*f(x)=ax^2+bx+c*
Forma factorizada
Una función cuadrática puede escribirse en forma factorizada, utilizando sus raíces, de la siguiente forma:
*f(x)=a(x-x_1)(x-x_2)*
donde a es el coeficiente principal y x1, x2 son las raíces de f. Si el discriminante es cero, ocurrirá que x1=x2 y la ecuación adquiere la forma:
*f(x)=a(x-x_1)^2*
Es de esperar que, si una función cuadrática no tiene raíces reales, entonces no puede escribirse en forma factorizada.
Forma normal o canónica
Si el vértice de una función cuadrática tiene coordenadas (h, k) podemos escribir la ecuación como:
*f(x)=a(x-h)^2+k*
Esta recibe el nombre de forma normal o canónica.
Si sabemos cuál es el vértice, podemos llegar rápidamente a esta expresión; si no lo sabemos, podemos operar con la forma polinómica en un proceso conocido como completar el cuadrado para llegar a la forma canónica.
Bibliografía
- Chorny, F., Casares, P. y Salpeter, C. (2015). Matemática 4. Editorial Estrada.
- Effenberger, P. (2016). Matemática III. Kapelusz Editora.
- Entre Números III. (2016). Santillana.
- Stewart, J. (2012). Cálculo de una variable, trascendentes tempranas (7ma edición). Cengage Learning.
- Thomas, G. (2006). Cálculo, una variable (11a edición). Pearson Educación.
Subir





Deja una respuesta