
Subconjunto de un conjunto
En este artículo explicamos qué es un subconjunto de un conjunto, los tipos que existen con ejemplos y las propiedades que cumplen.
Índice
¿Qué es un subconjunto?
Un conjunto es subconjunto de otro si todo elemento del primero es también un elemento del segundo, esta relación se simboliza con ⊆:
*A ⊆ B~* si y sólo si *~∀x: (x∈A → x∈B)*
Si existe al menos un elemento de A que no está en B, entonces se dice que A no es un subconjunto de B y se simboliza como A ⊈ B.
Ejemplos
- El conjunto A = {a, b} es subconjunto de B = {a, b, c, d} porque los elementos de A están también dentro de B, entonces A ⊆ B.
- El conjunto C = {0, 1, 2, 3} es un subconjunto de D = {-1, 0, 1, 2, 3, a, b}, porque todo elemento de C también está contenido en D, entonces C ⊆ D.
- El conjunto P = {p, q, r, s} no es un subconjunto de Q = {p, r} porque P tiene elementos que no están en Q, entonces: P⊈Q. Sin embargo, podemos notar que Q sí es un subconjunto de P, entonces Q⊆P.
- El conjunto de todos los mamíferos tiene por subconjunto al conjunto de todos los seres humanos, porque todo ser humano es un mamífero.
- El conjunto M = {-1, 1} es un subconjunto de N = {1, -1}, y a su vez N es un subconjunto de M. Esto ocurre porque ambos conjuntos son iguales, entonces M ⊆ N, N ⊆ M y M=N.
- El conjunto de los números naturales es un subconjunto del conjunto de los números enteros, pues todo número natural es también un número entero, entonces N ⊆ Z. Sin embargo, como existen enteros que no son naturales (los negativos y el cero), la relación recíproca no es cierta, Z no es subconjunto de N: Z ⊈ N.
- El conjunto de todos los reales positivos *\mathbb{R}^+* es un subconjunto de números reales, porque todo número real positivo es también un número real: *\mathbb{R}^+⊆\mathbb{R}.*
- Si llamamos T al conjunto de todos los triángulos, se tiene que el conjunto E de los triángulos equiláteros es un subconjunto de T: E ⊆ T.
Para demostrar que un conjunto es subconjunto de otro basta con probar que todo elemento del primero es también un elemento del segundo.
El conjunto que contiene a todos los subconjuntos de A se llama conjunto potencia o conjunto de partes de A, y se simboliza como P(A). Si A tiene n elementos, su conjunto potencia tiene *2^n* elementos. Es decir, el número de subconjuntos de un conjunto de n elementos es *2^n.*
Subconjunto propio
Un conjunto es subconjunto propio de otro si todos los elementos del primero son también elementos del segundo, pero existen elementos del segundo que no están en el primero, es decir que no pueden ser conjuntos iguales. Esta relación se simboliza con ⊂:
*A ⊂ B~* si y solo si *~∀x: (x∈A → x∈B)* y además *A\neq B*
Si existe al menos un elemento de A que no está en B, o ocurre que A y B son iguales, entonces se dice que A no es un subconjunto propio de B y se simboliza como A ⊄ B.
Ejemplos:
- El conjunto A = {a, b} es subconjunto propio de B = {a, b, c, d} porque los elementos de A están también dentro de B y hay elementos de B que no están en A ("c" y "d"). Entonces A ⊂ B. Nótese que también ocurre que A ⊆ B.
- El conjunto M = {-1, 1} es no es un subconjunto propio de N = {1, -1} porque ambos conjuntos son iguales, entonces M ⊄ N. Sin embargo, ocurre que M ⊆ N, es decir, M es subconjunto de M, pero no es un subconjunto propio.
- El conjunto de los números naturales, además de ser un subconjunto de los números enteros, también es un subconjunto propio de él: N ⊂ Z.
Todo subconjunto propio es también un subconjunto, como en el primer ejemplo, pero no todo subconjunto es un subconjunto propio, como en el segundo ejemplo.
Propiedades de los subconjuntos
Los subconjuntos cumplen con las propiedades de la inclusión de conjuntos:
- Todo conjunto es subconjunto de sí mismo, es decir, A ⊆ A.
- Si un conjunto es subconjunto de otro y este también es subconjunto del primero, entonces ambos conjuntos son iguales. Es decir, si A ⊆ B y B ⊆ A, entonces A=B.
- Si un conjunto es subconjunto de otro, y éste a su vez es subconjunto de un tercero, entonces el primer conjunto también es subconjunto del tercero. Es decir, si A ⊆ B y B ⊆ C, entonces A ⊆ C.
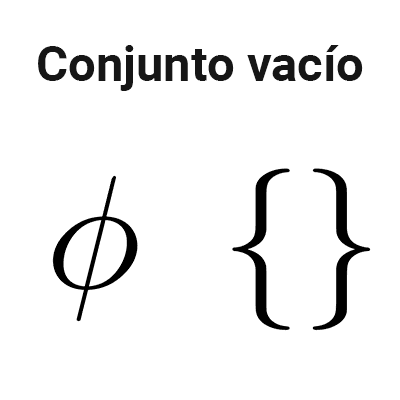
- El conjunto vacío es subconjunto de cualquier conjunto, hasta de sí mismo. O sea, Ø ⊆ A y Ø ⊆ Ø.
- Todos los conjuntos son subconjuntos del universal U: A ⊆ U.
Simbología
A continuación, se resume la simbología utilizada para referirnos a subconjuntos.
| Símbolo | Significado |
|---|---|
| A ⊆ B | A es subconjunto de B |
| A ⊈ B | A no es subconjunto de B |
| A ⊂ B | A es un subconjunto propio de B |
| A ⊄ B | A no es un subconjunto propio de B |
Bibliografía
- Corral de Franco, Y. y Manzanares, L. (2018). Nociones Elementales de lógica matemática y teoría de conjuntos. Caracas. Fondo editorial OPSU.
- Daun, J. y Falcón, Y. (1995). Lógica matemática. Universidad Autónoma Metropolitana.
- Gentile, E. (1984). Notas de Álgebra I. Editorial Universitaria de Buenos Aires.
- Grimaldi, R. (1997). Matemáticas discreta y combinatoria (3ra edición). Addison-Wesley Iberoamericana.
- Moreno, A. (1969). Lógica matemática: antecedentes y fundamentos. Editorial Universitaria de Buenos Aires.
- Puyau, H. y Roetti, J. (1976). Elementos de Lógica Matemática. Editorial Universitaria de Buenos Aires.
- Rojo, A. (1996). Álgebra I (18a edición). El Ateneo.
- Vidal, J. (2010). Teoría de conjuntos. Universidad de Valencia.
- Wilches, L., Costa, R., Rincón, M., Acosta, M., Roa, J., Sulvara, J. y Jaime, D. (2013). Matemática 6. Editorial Santillana.
- Zill, D. y Dewar, J. (2012). Álgebra, trigonometría y geometría analítica (3ra edición). McGraw Hill.
Subir






Deja una respuesta