
Función cúbica
En este artículo explicamos qué son las funciones cúbicas y cuáles son sus características y aplicaciones con ejemplos y gráficas.
Índice
¿Qué es una función cúbica?
Una función cúbica es una función polinómica de tercer grado, es decir, que puede ser escrita de la forma f(x)=ax3+bx2+cx+d donde a, b, c y d son números reales llamados coeficientes y a≠0. El número a que está multiplicando a x3 se llama coeficiente principal.
Algunos ejemplos de funciones cúbicas son:
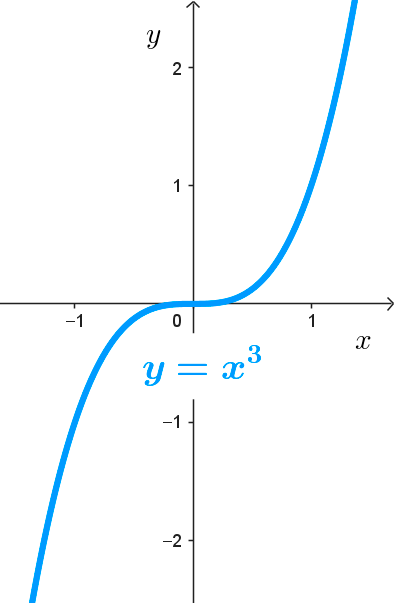
- *y=x^3*
- *y=-x^3*
- *y=x^3+3*
- *y=-x^3-3x*
- *y=2x^3+5x^2-3x+2*
- *y=-6x^3-3x^2+1*
- *y=-x^3-2x+6*
Las funciones cúbicas tienen diversas aplicaciones, por ejemplo, para calcular volúmenes de objetos y estructuras que tienen una forma cúbica o que están compuestos por formas cúbicas, como cajas, habitaciones o contenedores. Asimismo, son útiles en el diseño de estructuras, ya que una relación cúbica puede ofrecer tanto estética como funcionalidad.
Características
Las características y propiedades de una función cúbica son las siguientes:
- Dominio y rango: toda función cúbica tiene por dominio y rango al conjunto de los números reales.
- Gráfica: la gráfica de una función cúbica es una curva suave y continua.
- Intersección con el eje y: ocurre en el punto (0, d), donde d es el término independiente.
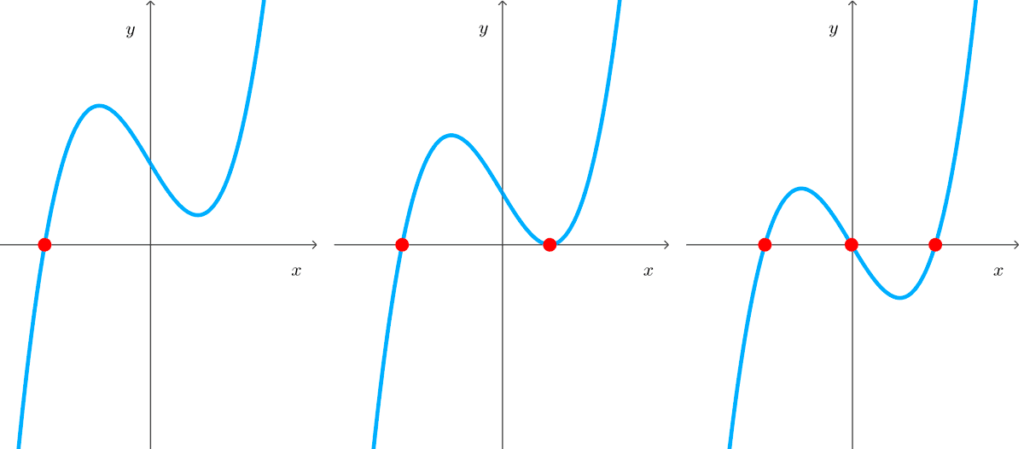
- Ceros o raíces: las funciones cúbicas pueden de uno a tres cortes con el eje x.
- Continuidad: las funciones cúbicas son continuas en todo su dominio.
- Simetría: las funciones cúbicas de la forma y=ax3+cx son impares, es decir, simétricas respecto al origen de coordenadas.
- Concavidad: toda función de tercer grado tiene un intervalo donde es cóncava hacia arriba (convexa) y otro donde es cóncava hacia abajo (cóncava).
- Punto de inflexión: toda función cúbica tiene un punto de inflexión que es donde cambia su concavidad.
- Máximos y mínimos: las funciones cúbicas pueden tener un punto máximo local en su sección cóncava y un punto mínimo local en su sección convexa, aunque no se da en todos los casos.
- Crecimiento y decrecimiento: una función de tercer grado puede tener intervalos donde es creciente y otros donde es decreciente, también puede ser creciente o decreciente en todo su dominio.
- Asíntotas: las funciones cúbicas no tienen asíntotas horizontales, verticales ni oblicuas.
Para encontrar los ceros de una función cúbica se puede recurrir a una factorización o a la regla de Ruffini. Lo que se busca es resolver la ecuación cúbica ax3+bx2+cx+d=0. Si se conocen las raíces de una función de tercer grado, esta puede escribirse en forma factorizada así:
*f(x)=a(x-x_1)(x-x_2)(x-x_3)*
donde *x_1, x_2, x_3* son las raíces de f.
Cuando a una función de tercer grado le faltan uno o varios términos, se llama función cúbica incompleta. Algunos casos que pueden darse son:
- Falta el término cuadrático: *y=ax^3+cx+d*
- Falta el término lineal: *y=ax^3+bx^2+d*
- Falta el término independiente: *y=ax^3+bx^2+cx*
- Faltan los términos cuadrático y lineal: *y=ax^3+d*
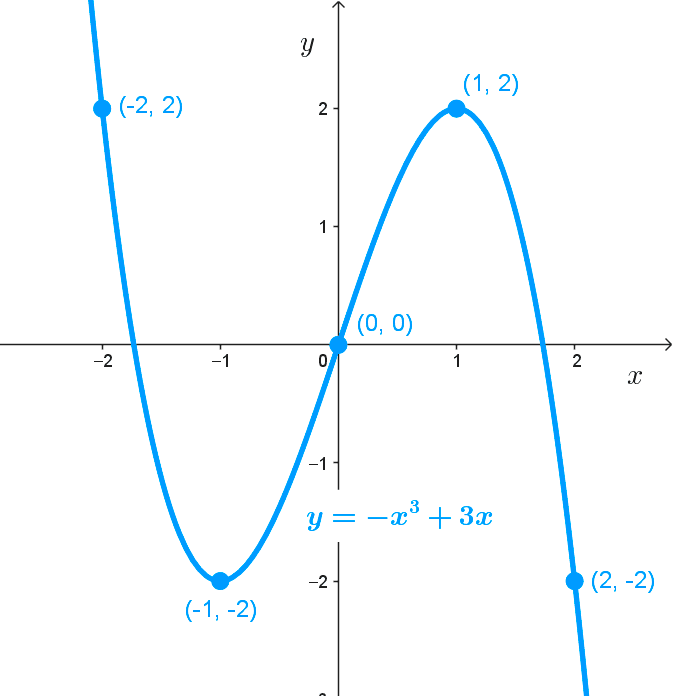
Para graficar una función cúbica se puede recurrir a una tabla de valores para conocer algunos puntos de la gráfica y luego trazar una curva suave que pase por ellos. Por ejemplo, para *y=-x^3+3x,* una tabla de valores sería la siguiente:
| x | y | (x, y) |
|---|---|---|
| -2 | 2 | (-2, 2) |
| -1 | -2 | (-1, -2) |
| 0 | 0 | (0, 0) |
| 1 | 2 | (1, 2) |
| 2 | -2 | (2, -2) |
Tal como sucede con cualquier otra función, es posible llevar a cabo operaciones algebraicas con funciones cúbicas como sumar, restar, multiplicar y dividir. Se debe tener en cuenta el dominio de las funciones originales para asegurar la existencia de la función resultante.
Ejemplos y gráficas
A continuación, veremos algunos ejemplos y gráficas de funciones cúbicas junto con su análisis correspondiente.
Ejemplo 1
*y=-x^3*
Análisis de la función:
- Dominio: *\mathbb{R}*
- Rango: *\mathbb{R}*
- Raíz: *x=0*
- Intersección con el eje y: *(0, 0)*
- Intervalos de crecimiento: la función no crece.
- Intervalo de decrecimiento: *(-\infty, +\infty)=\mathbb{R}*
- Simetría: la función es impar.
- Concavidad hacia arriba: *(-\infty, 0]*
- Concavidad hacia abajo: *[0, +\infty)*
- Punto de inflexión: en *x=0*
- Máximo: no tiene.
- Mínimo: no tiene.
- Asíntotas: no tiene.
Ejemplo 2
*y=x^3+2x^2*
Análisis de la función:
- Dominio: *\mathbb{R}*
- Rango: *\mathbb{R}*
- Raíces: *x=-2* y *x=0*
- Intersección con el eje y: *(0, 0)*
- Intervalos de crecimiento: *(-\infty, -\frac{4}{3})~* y *~(0,+\infty)*
- Intervalo de decrecimiento: *(-\frac{4}{3}, 0)*
- Simetría: la función no es par ni impar.
- Concavidad hacia abajo: *(-\infty, -\frac{2}{3}]*
- Concavidad hacia arriba: *[-\frac{2}{3}, +\infty)*
- Punto de inflexión: en *x=-\frac{2}{3}*
- Máximo local: en *x=-\frac{4}{3}*
- Mínimo local: en *x=0*
- Asíntotas: no tiene.
Ejemplo 3
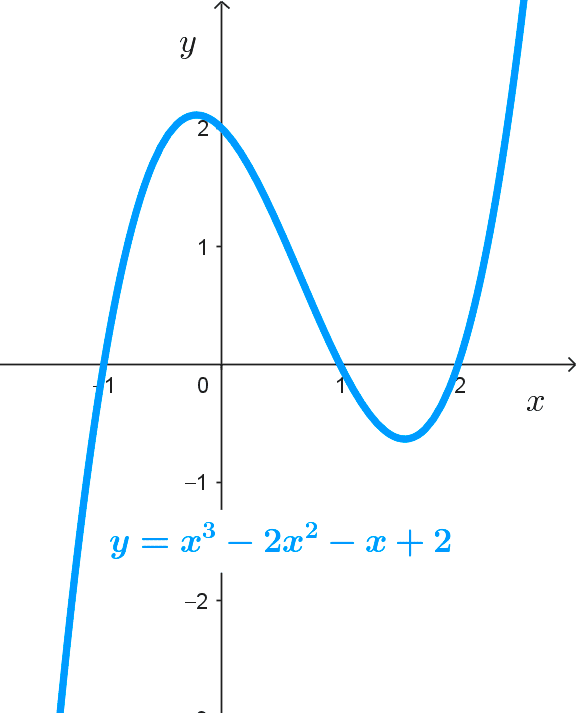
*y=x^3-2x^2-x+2*
Análisis de la función:
- Dominio: *\mathbb{R}*
- Rango: *\mathbb{R}*
- Raíces: *x=-1, x=1, x=2*
- Intersección con el eje y: *(0, 2)*
- Intervalos de crecimiento: *(-\infty; -0,22)* y *(1,55; +\infty)*
- Intervalo de decrecimiento: *(-0,22; 1,55)*
- Simetría: la función no es par ni impar.
- Concavidad hacia abajo: *(-\infty, \frac{2}{3}]*
- Concavidad hacia arriba: *[\frac{2}{3}, +\infty)*
- Punto de inflexión: en *x=\frac{2}{3}*
- Máximo local: en *x≈-0,22*
- Mínimo local: en *x≈1,55*
- Asíntotas: no tiene.
Otros ejemplos
Ejercicio para practicar
Ejercicio: determine cuáles de las siguientes son funciones cúbicas.
- *y=\sqrt{x^3}+3*
- *y=(x-3)^3+1*
- *y=\dfrac{1}{x^3+2x^2}*
- *y=x^3+3x^3+2x^3-9x^3+\sqrt{2}*
- *y=(x-1)^2(x-2)*
Soluciones:
- No es una función cúbica porque no es polinómica, la variable se encuentra dentro de una raíz.
- Es una función cúbica, desarrollando se puede escribir en forma estándar como *y=x^3-9x^2+27x-26.*
- No es una función cúbica porque la variable se encuentra en un denominador.
- Es una función cúbica, se puede escribir simplificada como *y=-3x^3+\sqrt{2}.*
- Es una función cúbica, desarrollando se llega a la expresión *y=x^3-4x^2+5x-2.*
Bibliografía
- Larson, R. y Edwards, B. (2010). Cálculo 1 de una variable (9na edición). McGraw Hill.
- Leithold, L. (1998). El Cálculo (7ma edición). Oxford University Press.
- Rabuffetti, H. (1999). Introducción al Análisis Matemático: Cálculo 1 (15a edición). El Ateneo.
- Stewart, J. (2012). Cálculo de una variable, trascendentes tempranas (7ma edición). Cengage Learning.
- Thomas, G. (2006). Cálculo, una variable (11a edición). Pearson Educación.
- Zill, D. y Wright, W. (2011). Cálculo, trascendentes tempranas (4ta edición). McGraw Hill.
Subir

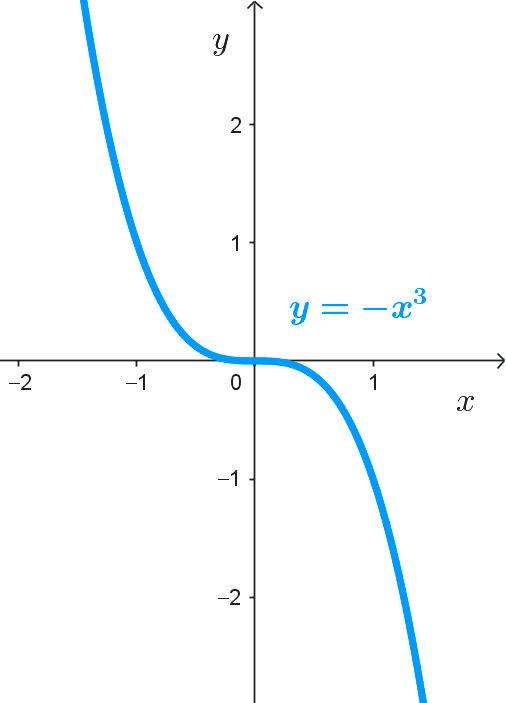






Deja una respuesta