
Codominio de una función
En este artículo explicamos qué es el codominio de una función, cuál es su diferencia con el dominio y el rango y algunos ejemplos.
Índice
¿Qué es el codominio?
El codominio de una función es el conjunto de llegada de la misma, es decir, aquél que contiene al rango, el cual es el conjunto de todos los valores que puede tomar la variable dependiente. El codominio de una función f se simboliza como Codf.
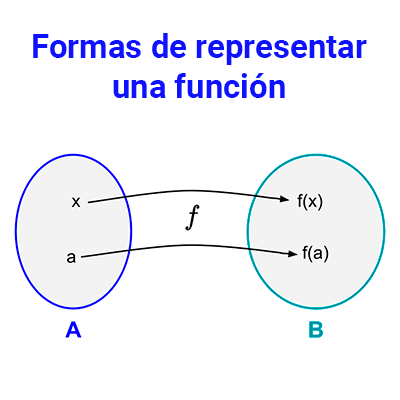
Recordemos que una función es una regla que asigna a todo elemento de un conjunto A un único elemento de un conjunto B. El conjunto A es llamado dominio, mientras que el conjunto B recibe el nombre de codominio.
En funciones reales se considera como codominio al conjunto de los números reales *\mathbb{R},* al menos que se indique lo contrario. La diferencia principal entre el codominio y el rango (o imagen) es que el rango es un subconjunto del codominio y no son necesariamente iguales. Puede ocurrir que existan elementos del codominio que no están en el rango de la función.
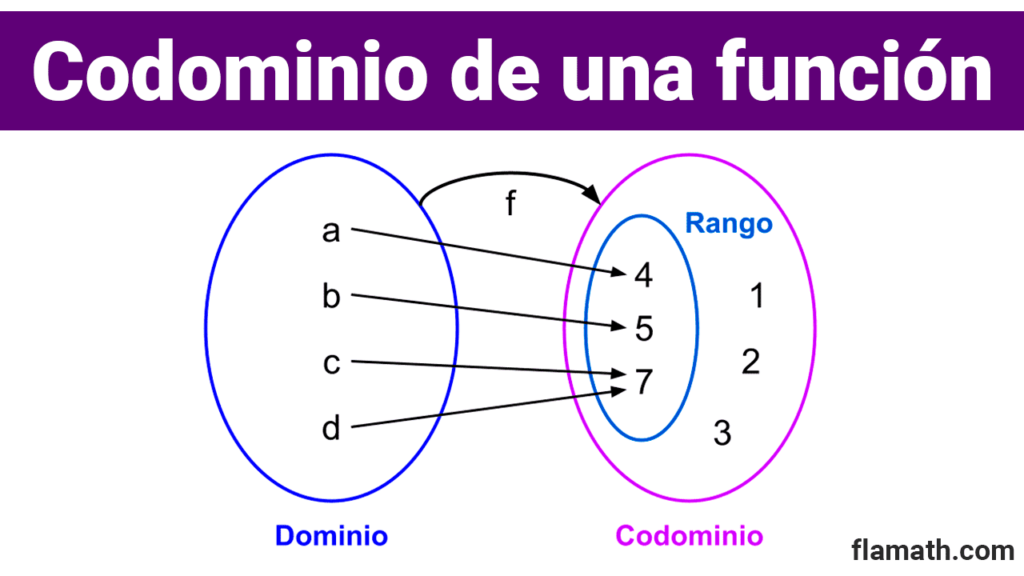
Analizando el diagrama:
- El conjunto A es el dominio de la función. A={a, b, c, d}.
- El conjunto B es el codominio de la función. B={1, 2, 3, 4, 5, 7}.
- El rango de la función está dentro del codominio y es R={4, 5, 7}.
La importancia del codominio radica en que, si es igual al rango, la función es sobreyectiva, el cual es uno de los requisitos para que la función tenga una inversa. Si el codominio y el rango son diferentes, se puede realizar una restricción del codominio para solucionarlo, logrando que la función sea sobreyectiva.
Por ejemplo, la función cuadrática *f(x)=x^2* tiene como dominio y codominio al conjunto de los números reales. El rango es el conjunto de los reales no negativos *[0,+∞).* La función no es biyectiva porque existen valores del dominio que tienen la misma imagen (como -2 y 2) y porque el codominio no es igual al rango. En estas condiciones, la función no tiene inversa.
Sin embargo, podemos realizar una restricción de dominio y de codominio para que la función pase a ser biyectiva. Si hacemos *D_f=[0,+∞)* y *Cod_f=[0,+∞),* el codominio y el rango coinciden, y no hay valores del dominio que tengan la misma imagen. Ahora, la función es biyectiva y su inversa es la función raíz cuadrada *f^{-1}(x)=\sqrt{x}.*
Ejemplos
Como dijimos, el codominio de una función real se considera como el conjunto de los números reales, salvo que se explicite lo contrario. Así, las funciones algebraicas (polinómicas, constantes, lineales, cuadráticas, racionales, irracionales, etc.) y las funciones trascendentes (exponenciales, logarítmicas, trigonométricas e hiperbólicas) tienen como codominio al conjunto de los números reales.
En la siguiente tabla se muestran ejemplos de funciones reales y sus dominios, codominios y rangos.
| Función | Dominio | Codominio | Rango |
|---|---|---|---|
| *y=2x+1* | *\mathbb{R}* | *\mathbb{R}* | *\mathbb{R}* |
| *y=3* | *\mathbb{R}* | *\mathbb{R}* | *\{3\}* |
| *y=x^2* | *\mathbb{R}* | *\mathbb{R}* | *[0, +∞)* |
| *y=1/x* | *\mathbb{R}-\{0\}* | *\mathbb{R}* | *\mathbb{R}-\{0\}* |
| *y=\sqrt{x-1}* | *[1, +∞)* | *\mathbb{R}* | *[0, +∞)* |
| *y=e^x* | *\mathbb{R}* | *\mathbb{R}* | *(0, +∞)* |
| *y=\ln(x)* | *(0, +∞)* | *\mathbb{R}* | *\mathbb{R}* |
| *y=\cos(x)* | *\mathbb{R}* | *\mathbb{R}* | *[-1,1]* |
Bibliografía
- Edwards, C. y Penney, D. (1997). Cálculo Diferencial e Integral (4ta edición). Pearson Educación.
- Piskunov, N. (1977). Cálculo diferencial e integral (3ra edición). Editorial Mir Moscú.
- Rabuffetti, H. (1999). Introducción al Análisis Matemático: Cálculo 1 (15a edición). El Ateneo.
- Sadosky, M. y Guber, R. (1984). Elementos de cálculo diferencial e integral (17a edición). Librería y Editorial Alsina.
- Stewart, J. (2012). Cálculo de una variable, trascendentes tempranas (7ma edición). Cengage Learning.
- Thomas, G. (2006). Cálculo, una variable (11a edición). Pearson Educación.





Deja una respuesta