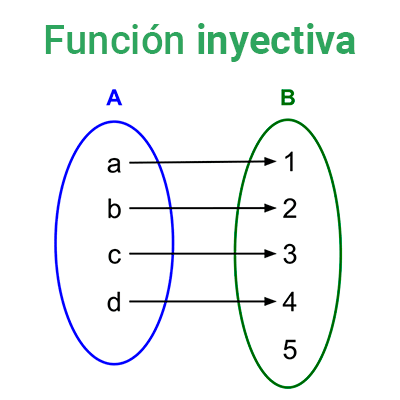
Función sobreyectiva
En este artículo explicamos qué es una función sobreyectiva con ejemplos y cómo determinar si una función es sobreyectiva o no.
Índice
¿Qué es una función sobreyectiva?
Una función sobreyectiva es aquella en la que el codominio es igual al rango, es decir, todo elemento del codominio es imagen de algún elemento del dominio. Otras formas de llamar a una función sobreyectiva son: suprayectiva, suryectiva, subyectiva, epiyectiva o exhaustiva.
Formalmente, una función f con dominio A y codominio B es sobreyectiva si se cumple que:
*∀y∈B~ ∃x∈A~:~y=f(x)*
Es decir, para todo elemento y en B existe al menos un elemento x en A tal que y es la imagen de x a través de f.
Es importante no confundir la sobreyectividad con el postulado de existencia de una función. Para hablar de función, todo elemento del dominio debe tener un correspondiente en el codominio; pero para hablar de función sobreyectiva, también todo elemento del codominio debe tener un correspondiente en el dominio.
Una función donde al menos un elemento del codominio no es elemento del rango se llama función no sobreyectiva. Por ejemplo, la función *y=x^2,* si consideramos como codominio al conjunto de los números reales, no es sobreyectiva porque su rango son solo los reales no negativos, por tanto el codominio tiene más elementos que el rango.
La importancia de que una función sea sobreyectiva radica en que es uno de los requisitos para que exista su función inversa, el otro requisito es que sea inyectiva. Una función que es sobreyectiva e inyectiva a la vez se llama biyectiva.
Un ejemplo de función sobreyectiva en la vida cotidiana podría ser el proceso de entrega de correo: cada cartero tiene asignada una dirección para hacer entregas, y ninguna dirección se queda sin un cartero que realice las entregas. Por lo tanto, todas las direcciones (codominio) están cubiertas por los carteros (dominio), haciendo que la asignación sea sobreyectiva.
¿Cómo saber si una función es sobreyectiva?
Para determinar si una función es sobreyectiva, se debe verificar que el codominio y el rango sean el mismo conjunto de valores. Si los conjuntos son diferentes, entonces la función no es sobreyectiva.
En funciones reales de variable real, se considera que el codominio de toda función es el conjunto de los números reales, al menos que se explicite lo contrario. Cuando no se especifica el codominio, la sobreyectividad consiste en que el rango sea igual al conjunto de los números reales.
Ejemplo 1: determinar si la función valor absoluto *f(x)=|x|* es sobreyectiva.
Solución: como no se explicita nada, consideraremos que el codominio de f es el conjunto de los números reales: *Cod_f=\mathbb{R}.* Ahora bien, el valor absoluto de un número real es siempre un número no negativo, por lo tanto, el rango de f es *R_f=[0,+∞).*
Resulta claro que el codominio y el rango son diferentes, pues *\mathbb{R}\neq [0,+∞).* Entonces, la función valor absoluto no es sobreyectiva.
Ejemplo 2: analizar si la siguiente función es sobreyectiva.
*f: \mathbb{R}→[0,+\infty)~/~f(x)=\sqrt{x}*
Solución: en este caso se especifica que el codominio de la función es el intervalo *[0,+\infty).* Como la función raíz cuadrada arroja como resultados sólo valores no negativos, su rango el también el intervalo *[0,+\infty).* Como el codominio y el rango son iguales, la función es sobreyectiva.
Ejemplo 3: probar si la función *y=x^3* es sobreyectiva.
Solución: no se especifica el codominio, por tanto, lo tomamos como el conjunto *\mathbb{R}.* Ahora, como el rango de toda función cúbica es también el conjunto *\mathbb{R},* la función es sobreyectiva.
Restricciones de codominio
Una función que no es sobreyectiva puede convertirse en una que sí lo es restringiendo su codominio. La idea básica es definir como nuevo codominio al rango de la función.
Por ejemplo, hace un momento vimos que la función valor absoluto *f(x)=|x|* no es sobreyectiva, pues su codominio es *\mathbb{R}* y su rango es *[0,+∞).* Sin embargo, podemos definir una restricción del codominio haciendo que sea igual al rango. De este modo, el nuevo codominio es *[0,+∞)* y la función obtenida es sobreyectiva.
Otro caso es con la función cuadrática *y=x^2.* Su codominio es *\mathbb{R}* y su rango es *[0,+∞),* pero si restringimos el codominio a solo los reales no negativos, *[0,+∞),* la función obtenida cumple con la sobreyectividad.
Ejemplos
Las siguientes afirmaciones pueden ser de utilidad a la hora de determinar si una función es sobreyectiva o no. Se considera como codominio al conjunto de los números reales.
- Todas las funciones lineales no constantes son sobreyectivas.
- Las funciones constantes no son sobreyectivas.
- Las funciones potenciales de la forma *y=x^n,* donde n es un entero positivo, son sobreyectivas cuando n es impar y no son sobreyectivas cuando n es par.
- Las funciones logarítmicas son sobreyectivas, las exponenciales no lo son (a menos que se restrinja su codominio).
- Las funciones radicales de la forma *y=\sqrt[n]{x},* donde n es un entero positivo, son sobreyectivas sin n es impar y no son sobreyectivas si n es par.
- Las funciones trigonométricas seno y coseno no son sobreyectivas, pero es posible realizar restricciones de codominio para que lo sean. La función tangente es sobreyectiva.
Ejemplos de funciones sobreyectivas:
- *y=x+1*
- *y=-x+6*
- *y=2x^3+5*
- *y=\sqrt[3]{x}*
- *y=\ln(x)*
Ejemplos de funciones no sobreyectivas:
- *y=3*
- *y=x^2+3*
- *y=e^x*
- *y=\cos(x)*
- *y=\dfrac{1}{x}*
Ejemplos de funciones sobreyectivas pero no inyectivas:
- *y=\tan(x)*
- *y=3x^3+6x^2*
- *y=x^5+x^2*
Preguntas frecuentes
¿Cuál es la diferencia entre una función sobreyectiva y una función inyectiva?
Una función sobreyectiva asegura que cada elemento del codominio tenga al menos un elemento del dominio que le corresponde. En contraste, una función inyectiva garantiza que dos elementos del dominio no tengan la misma imagen.
¿Cuál es la diferencia entre una función sobreyectiva y una función biyectiva?
Una función sobreyectiva cubre todo el codominio, pero puede tener elementos en el dominio que se asignan a más de un elemento en el codominio. Por otro lado, una función biyectiva es tanto inyectiva como sobreyectiva, lo que significa que cada elemento del dominio se asigna a un único elemento en el codominio y viceversa, sin dejar elementos sin asignar en ninguno de los conjuntos.
