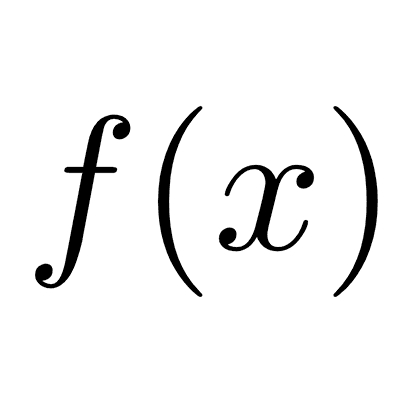
Propiedades de las funciones

En este artículo explicamos cuáles son las propiedades de las funciones matemáticas con ejemplos de cada una.

Índice

Propiedades

Al analizar una función podemos encontrarnos con una serie de características distintivas. Entre las propiedades de una función tenemos:

Dominio: es el conjunto de partida que contiene todos los valores para los cuales la función está definida.
Codominio: es el conjunto de llegada de la función.
Rango: es el conjunto de todos los valores que la función produce como resultado.
Signo: describe si la función es positiva o negativa en un intervalo dado.
Puntos de corte con los ejes: son los puntos donde la función interseca los ejes x e y.
Monotonía: describe si la función aumenta, disminuye o permanece constante en un intervalo dado.
Continuidad: indica si la función podría ser graficada en un solo trazo sin levantar el lápiz del papel.
Puntos extremos: son los valores máximos o mínimos que la función puede tomar.
Concavidad: describe si la gráfica de la función se curva hacia arriba o hacia abajo.
Acotación: indica si la función está limitada en su crecimiento o decrecimiento por ciertos valores.
Simetría: describe si la función exhibe algún tipo de simetría respecto al eje y o al origen de coordenadas.
Periodicidad: indica si la función se repite en intervalos regulares.
Comportamientos asintóticos: describe si la gráfica de la función se acerca a una recta a medida que la variable independiente se acerca a un valor, aumenta o disminuye sin límites.

Dominio, codominio y rango

El dominio de una función es el conjunto de partida que contiene todos los posibles valores de entrada para los cuales la función está definida. El codominio es el conjunto de llegada y el rango es un subconjunto del codominio que contiene todos los valores de salida de la función.

Para las funciones reales de variable real, el dominio y el rango son subconjuntos de números reales. Si una función no explicita su codominio, se considera que es el conjunto de los números reales.

Ejemplos

La función racional *f(x)=1/x* está definida para todos los números reales excepto el cero, entonces, su dominio es *D_f=\mathbb{R}-\{0\}.* El codominio, como no se especifica, es *\mathbb{R}.* Como valores de salida tenemos a todos los números reales menos el cero, por lo tanto, su rango es *R_f=\mathbb{R}-\{0\}.*
La función raíz cuadrada *y=\sqrt{x}* solo está definida para valores no negativos de x, por lo que su dominio es *D=[0,+\infty).* El codominio es *\mathbb{R}.* Como la raíz cuadrada arroja un resultado no negativo, el rango de la función es *R=[0,+\infty).*

Signo

Una función f es positiva en un intervalo si su gráfica se encuentra por encima del eje x en ese intervalo y se simboliza como f(x)>0. De forma análoga, la función es negativa en un intervalo si su gráfica se encuentra por debajo del eje x y se denota como f(x)<0. Los valores donde la gráfica corta al eje x son llamados raíces o ceros; en ellos, la función es cero: f(x)=0.

Puntos de corte con los ejes

La gráfica de una función puede cortar a los ejes cartesianos. La intersección con el eje x se da cuando y=0, los valores de x que anulan la función se llaman ceros o raíces. La intersección con el eje y se da cuando x=0; si esta intersección existe, es única.

Intersecciones de una función con el eje x

Intersección de una función con el eje y

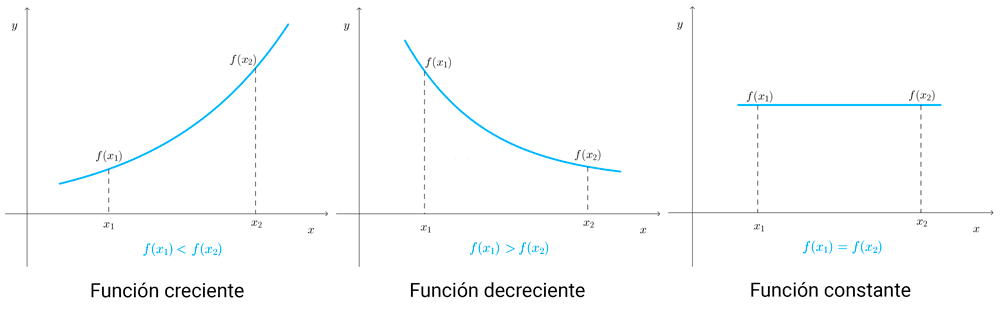
Monotonía

Una función es creciente en un intervalo si sus valores aumentan a medida que la variable independiente aumenta. Gráficamente, la curva de la función sube de izquierda a derecha.
Una función es decreciente en un intervalo si sus valores disminuyen a medida que la variable independiente aumenta. Gráficamente, la curva de la función baja de izquierda a derecha.
Una función es constante en un intervalo si sus valores son iguales en cualquier punto del intervalo. Gráficamente, la curva es un segmento de recta paralelo al eje x.

Formalmente, dada una función f y el intervalo I que pertenece a su dominio:

*f* es creciente en I si y solo si *f(x_1)<f(x_2)* siempre que *x_1<x_2* en I.
*f* es decreciente en I si y solo si *f(x_1)>f(x_2)* siempre que *x_1<x_2* en I.
*f* es constante si *f(x_1)=f(x_2)* para todo *x_1* y *x_2* en I.

Gráficas de función creciente, decreciente y constante

Una función se dice monótona si solo crece o solo decrece en todo su dominio. Si la función tiene intervalos de crecimiento y decrecimiento en su dominio, se dice que es no monótona.

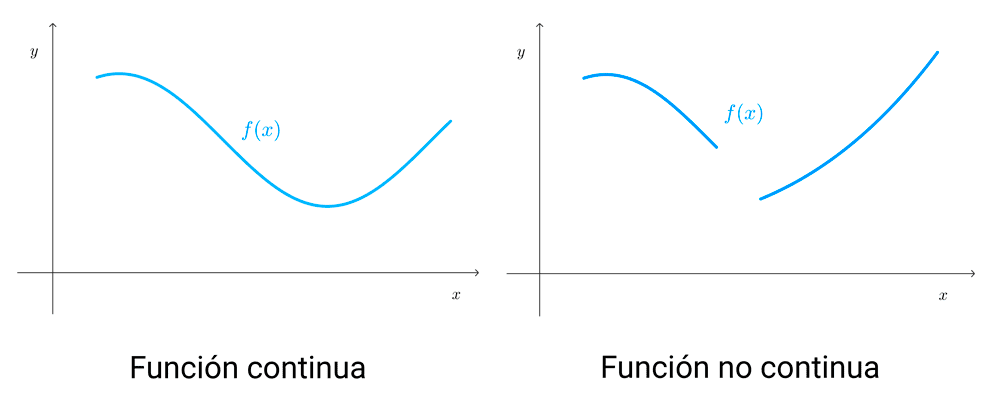
Continuidad

Una función continua es aquella que no presenta "saltos" o "interrupciones" en su gráfica. En otras palabras, podemos dibujar su gráfica sin levantar el lápiz del papel.

Gráficas de una función continua y una función discontinua

Ejemplos

Las funciones polinómicas (constantes, lineales, cuadráticas, cúbicas, etc.) son continuas en todo su dominio, por tanto, sus gráficas no presentan saltos.
La función *f(x)=|x|/x* presenta una discontinuidad en x=0 porque su gráfica "salta" de -1 hasta 1.

Puntos extremos

Los puntos extremos de una función son aquellos donde su valor alcanza el valor más grande o más pequeño posible. Estos puntos son importantes para analizar el comportamiento de la función. Existen cuatro tipos de puntos extremos:

Máximo local o relativo: es un punto donde la función alcanza un valor mayor que todos los valores de la función en un intervalo a su alrededor.
Mínimo local o relativo: es un punto donde la función alcanza un valor menor que todos los valores de la función en un intervalo a su alrededor.
Máximo absoluto o global: es el punto donde la función alcanza el valor más grande posible en todo su dominio.
Mínimo absoluto o global: es el punto donde la función alcanza el valor más pequeño posible en todo su dominio.

Extremos mínimos y máximos, absolutos y relativos de una función — Puntos extremos de una función

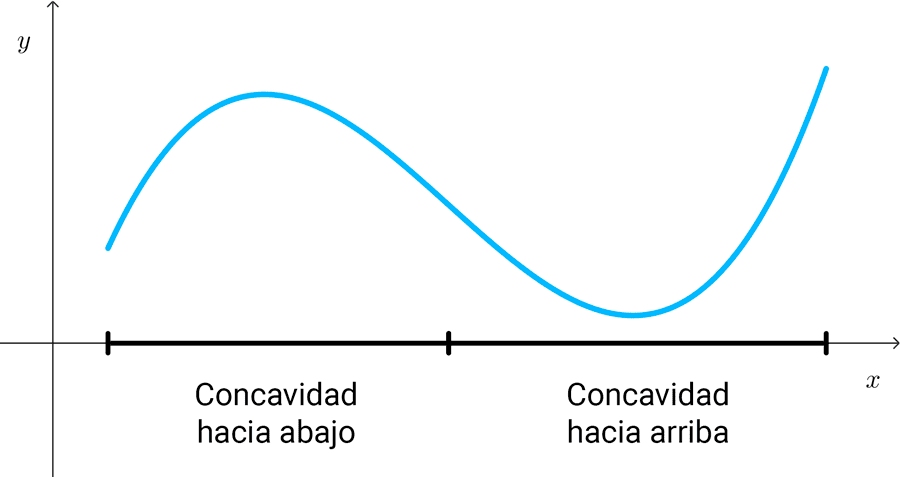
Concavidad

La concavidad de una función describe la forma de su gráfica, indicando si se curva hacia arriba o hacia abajo en diferentes intervalos de su dominio. En un intervalo, la función puede ser cóncava hacia arriba (con forma de U) o cóncava hacia abajo (con forma de ∩). Los puntos donde la concavidad cambia se llaman puntos de inflexión.

Función cóncava y convexa, cóncava hacia abajo y cóncava hacia arriba — Concavidad de una función

Acotación

Una función está acotada superiormente si existe un valor que las imágenes no superan, y está acotada inferiormente si sus imágenes se mantienen siempre por encima de cierto número. Se dice que una función está acotada si existen esos dos valores.

Formalmente, si f una función definida en un conjunto D, entonces:

f está acotada superiormente si existe un número real M tal que f(x)≤M para toda x en D. M recibe el nombre de cota superior.
f está acotada inferiormente si existe un número real m tal que f(x)≥m para toda x en D. El valor m recibe el nombre de cota inferior.
f es una función acotada si está acotada superior e inferiormente. Se cumple entonces que m≤f(x)≤M.

Ejemplo

Función trigonométrica coseno acotada — La función coseno está acotada entre -1 y 1. La cota inferior es -1 y la cota superior es 1.

Simetría

La simetría de una función se refiere a la propiedad que tiene su gráfica de coincidir consigo misma al ser reflejada respecto a un eje o un punto. Existen dos tipos principales de funciones según su simetría:

Funciones pares: son aquellas simétricas respecto al eje y.
Funciones impares: son aquellas simétricas respecto al origen de coordenadas.

Gráfica de una función par — Función par

Gráfica de una función impar — Función impar

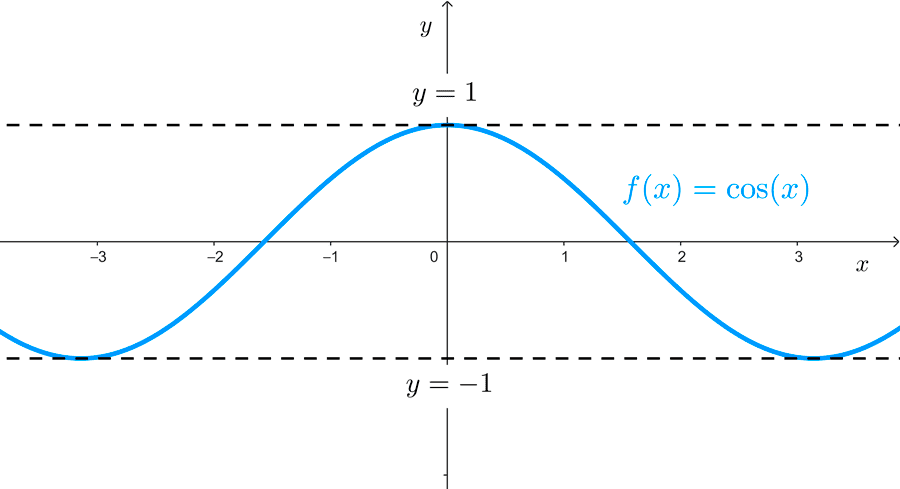
Periodicidad

Las funciones periódicas son aquellas que repiten sus valores en intervalos regulares. Esto significa que para cualquier valor del dominio, la función produce el mismo valor después de cierto intervalo.

Formalmente, una función *f* es periódica con período T si se cumple que *f(x+T)=f(x)* para toda *x* del dominio. El número T es positivo y se llama período de la función. Al valor más pequeño del período se le llama período fundamental.

Ejemplo

Función trigonométrica seno periódica — La función seno es periódica con período fundamental 2π porque para toda a se cumple que sin(a+2π)=sin(a)

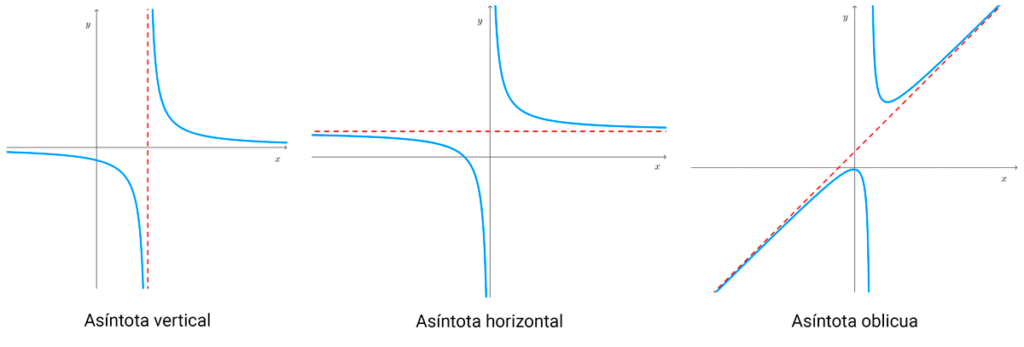
Asíntotas

Una asíntota es una recta a la que la gráfica de una función se acerca a medida que el valor de la variable independiente se acerca a un valor específico o se aleja hacia el infinito. Existen tres tipos de asíntotas:

Asíntotas horizontales: son líneas horizontales a las que la gráfica se acerca cuando la variable independiente tiende a infinito positivo o negativo.
Asíntotas verticales: son líneas verticales a las que la gráfica se acerca cuando la variable independiente se acerca a un determinado valor.
Asíntotas oblicuas: son líneas no horizontales ni verticales a las que la gráfica se acerca cuando la variable independiente tiende a infinito positivo o negativo.

La presencia de asíntotas es común en funciones racionales, aunque existen otros tipos de funciones que pueden tenerlas. Existen funciones que no tienen ninguna asíntota.