Funciones pares e impares
En este artículo explicamos el concepto y definición de funciones pares e impares acompañado de ejemplos, gráficos, formas de determinar la paridad y las propiedades matemáticas que cumplen estas funciones.
Índice
Definiciones
Una función par es aquella que satisface que cualquier valor de su dominio tiene la misma imagen que el valor opuesto. En símbolos:
*f(x)=f(-x)* para toda x del dominio
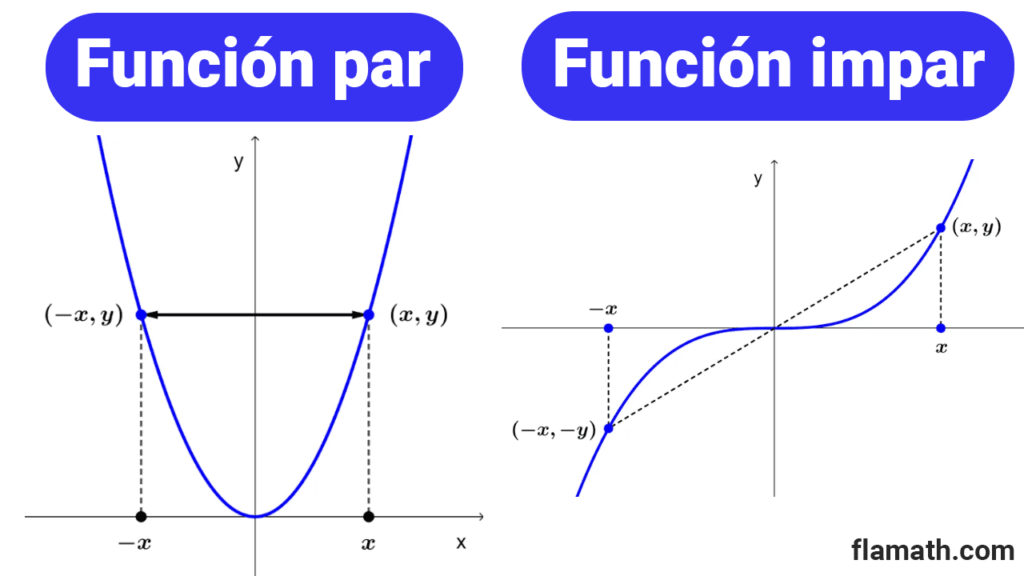
La gráfica de una función par cumple con la propiedad de ser simétrica respecto al eje y.
Una función impar es aquella que satisface que cualquier valor de su dominio tiene como imagen al opuesto de la imagen del valor opuesto. En símbolos:
*f(x)=-f(-x)* o equivalentemente *f(-x)=-f(x)* para toda x del dominio
La gráfica de una función impar es simétrica respecto al origen de coordenadas.
Los nombres de par e impar surgen de las potencias de x, pues podemos notar que las funciones de exponente par de x son funciones pares, y las de exponente impar son funciones impares:
- Dada *f(x)=x^2*, se puede ver que *f(-x)=(-x)^2=x^2=f(x)*, por ende cumple con la definición de función par.
- Dada *f(x)=x^3*, vemos que *f(-x)=(-x)^3=-x^3=-f(x)*, por tanto se trata de una función impar.
Lo mismo ocurre con otras potencias de la misma naturaleza, por ejemplo:
- *f(x)=x^5* es una función impar pues *f(-x)=(-x)^5=-x^5=-f(x)*
- *g(x)=x^8* es una función par ya que *g(-x)=(-x)^8=x^8=g(x)*
La importancia geométrica de una función par se debe a que su gráfica es simétrica con respecto al eje y. Es decir, si disponemos de la gráfica para *x≥0* (el lado derecho del plano), podemos obtener la gráfica completa reflejando esa parte con respecto al eje y. Dicho de otro modo, una reflexión respecto al eje de ordenadas deja sin cambios a la gráfica.
En el caso de una función impar, su gráfica es simétrica respecto al origen de coordenadas. Si disponemos de la gráfica para *x≥0*, podemos obtener la gráfica completa girando 180° ese tramo alrededor del origen de coordenadas.
¿Cómo saber si una función es par o impar?
Dada una función, si disponemos de la gráfica, podemos verificar si esta es simétrica respecto al eje y o respecto al origen de coordenadas para llegar a una conclusión sobre la paridad.
También podemos analizar algebraicamente si esta es par o impar hallando la imagen de -x y verificando si se cumple alguna de las definiciones. Existen funciones que no son pares ni impares, esto ocurre cuando no se cumplen ninguna de las definiciones.
Pasos para determinar algebraicamente si una función es par o impar
- Calcular la imagen de -x: esto se logra reemplazando x por -x en la ecuación.
- Simplificar la expresión resultante: realizar todas las operaciones para obtener una forma simple de la ecuación.
- Analizar la ecuación final: si la expresión es igual a la ecuación original, entonces la función es par. Si la expresión es opuesta a la ecuación original, entonces la función es impar. Si no ocurre ninguno de los casos anteriores, la función no es par ni impar.
Ejemplo 1: *f(x)=x^2+1*
Anteriormente vimos que *y=x^2* es una función par, veremos qué ocurre en este caso.
Calculamos *f(-x)*:
*f(-x)=(-x)^2+1=x^2+1=f(x)*
Como cumple la primera definición, *f* es una función par.
Ejemplo 2: *f(x)=\dfrac{1}{x}*
Tenemos una función racional, calculamos *f(-x)*:
*f(-x)=\dfrac{1}{-x}=-\dfrac{1}{x}=-f(x)*
Dado que cumple la segunda definición, la función es impar.
Ejemplo 3: *f(x)=3x^2+2x+1*
Calculamos *f(-x)*:
*f(-x)=3(-x)^2+2(-x)+1=3x^2-2x+1*
No se cumple ninguna de las definiciones, por lo tanto, la función no es ni par ni impar.
Ejemplo 4:
*f(x)=\begin{cases} -1 \hspace{5mm} \text{si} \ x<0 \\1 \hspace{7.5mm} \text{si} \ x>0 \end{cases}*
En este caso tenemos una función por partes, con lo cual tendremos que prestar más atención a la hora de verificar la paridad de la forma que veníamos haciendo.
Calculamos *f(-x)*:
Cuando *x<0, f(x)=-1,* pero *-x>0*, entonces *f(-x)=1=-f(x)* (en el primer tramo).
Cuando *x>0, f(x)=1,* pero *-x<0*, entonces *f(-x)=-1=-f(x)* (en el segundo tramo).
Por cumplirse la segunda definición en ambos tramos, la función por partes es impar.
Paridad de las funciones trigonométricas
Las funciones trigonométricas seno, coseno y tangente son impar, par e impar respectivamente. Esto por las propiedades que verifica el opuesto de un número en sus argumentos.
*f(x)=\sin{x}→f(-x)=\sin(-x)=-\sin{x}=-f(x).* Por tanto, el seno es una función impar.
*f(x)=\cos x→f(-x)=\cos(-x)=\cos x=f(x).* Por tanto, el coseno es una función par.
*f(x)=\tan x→f(-x)=\tan(-x)=-\tan x=-f(x).* Por tanto, la tangente es una función impar.
Se pueden demostrar igualmente las siguientes propiedades:
- La función cosecante es impar.
- La función secante es par.
- La función cotangente es impar.
Propiedades de las funciones pares e impares
Las funciones pares e impares cumplen con una serie de propiedades, ellas son:
- Toda función real es igual a la suma de una función par y una función impar.
- La función constante f(x) = 0 es la única que es par e impar al mismo tiempo.
- El producto de dos funciones pares es una función par.
- El producto de dos funciones impares es una función par.
- El producto de una función par y una función impar es una función impar.
- La suma de dos funciones pares es una función par.
- La suma de dos funciones impares es una función impar.
Demostraciones
Propiedad 1:
Se quiere demostrar que toda función con dominio *\mathbb{R}* se puede escribir como suma de una función par y una función impar. Esto puede lograr usando a la siguiente identidad:
*f(x)=\dfrac{1}{2}[f(x)+f(-x)]+\dfrac{1}{2}[f(x)-f(-x)]*
El primer corchete encierra a una función par y el segundo una función impar.
Por ejemplo, con *f(x)=3x^2+2x+1* podemos realizar los cálculos para descubrir que es la suma de la función par *3x^2+1* y la función impar *2x.*
Propiedad 2:
Se quiere demostrar que la función *f(x)=0* es la única que es par e impar al mismo tiempo.
En efecto, buscamos una función que cumpla *f(x)=f(-x)=-f(-x)*
De la segunda y tercera igualdad extraemos que un número debe ser igual a su opuesto, y esto solo ocurre cuando ese número es cero, entonces *f(x)=0*
Propiedad 3:
Buscamos demostrar que el producto de dos funciones pares es una función par.
En efecto, supongamos que dos funciones f y g son pares. Entonces ocurre que *f(x)=f(-x)* y *g(x)=g(-x)*.
Sea *h* la función producto: *h(x)=f(x)\cdot g(x).* Se verifica que *h(-x)=f(-x) \ g(-x)=f(x) \ g(x)=h(x).* Por tanto, h también es una función par.
Propiedad 4:
Se busca demostrar que el producto de dos funciones impares es una función par.
Supongamos que dos funciones f y g son impares. Entonces ocurre que *f(-x)=-f(x)* y *g(-x)=-g(x)*
Sea h la función producto: *h(x)=f(x) \cdot g(x).*
Se cumple que:
*h(-x)=f(-x) \cdot g(-x)*
*=[-f(x)] \cdot [-g(x)]*
*=(-1) f(x) \cdot (-1)g(x)*
*=(-1)(-1)f(x) \cdot g(x)*
*=f(x) \cdot g(x)*
*=h(x)*
Entonces, la función producto es par.
Propiedad 5:
Se quiere probar que el producto de una función par y una función impar es una función impar.
Sea *f* una función par y *g* una función impar. Se cumple que *f(-x)=f(x)* y *g(-x)=-g(x)*
Sea *h* la función producto: *h(x)=f(x) \cdot g(x)*
Se verifica que:
*h(-x)=f(-x) \cdot g(-x)*
*=f(x) \cdot [-g(x)]*
*=-[f(x) \cdot g(x)]*
*=-h(x)*
Entonces se demuestra que h es una función impar.
Propiedad 6:
Se quiere demostrar que la suma de dos funciones pares es una función par.
Sean *f* y *g* dos funciones pares. Entonces *f(-x)=f(x)* y *g(-x)=g(x)*
Sea h la función suma: *h(x)=f(x)+g(x)*
Se cumple que: *h(-x)=f(-x)+g(-x)=f(x)+g(x)=h(x)*
Entonces, la función suma es par.
Propiedad 7:
Se busca probar que la suma de dos funciones impares es una función impar.
Sean *f* y *g* dos funciones impares. Entonces *f(-x)=-f(x)* y *g(-x)=-g(x)*
Sea *h* la función suma: *h(x)=f(x)+g(x)*
Se verifica que: *h(-x)=f(-x)+g(-x)=-f(x)-g(x)=-[f(x)+g(x)]=-h(x)*
Entonces, la función suma es impar.
Subir
Deja una respuesta