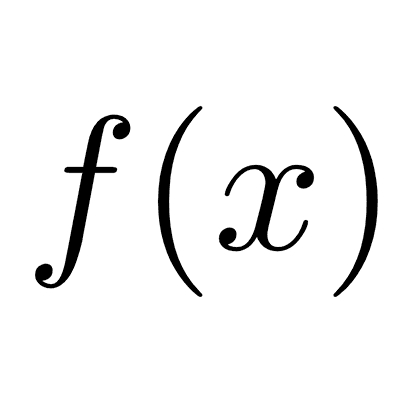
Funciones inyectivas, sobreyectivas y biyectivas
En este artículo explicamos la clasificación de funciones según la relación entre sus elementos en inyectivas, sobreyectivas y biyectivas. Analizamos las definiciones, ejemplos, cómo se comportan las gráficas y cómo reconocer a que grupo pertenece una función.
Índice
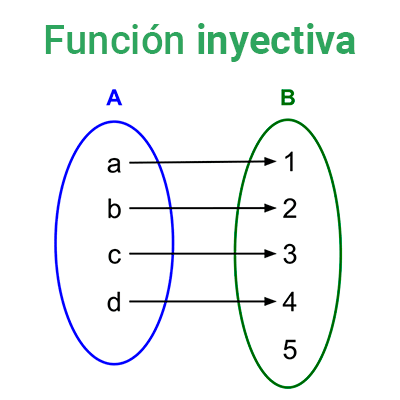
Función inyectiva
Una función f con dominio A y codominio B es inyectiva (o uno a uno) si ocurre que dos elementos distintos de su dominio siempre tienen imágenes distintas. En símbolos:
*f \ \text{es inyectiva}↔∀x_1∈A~∀x_2∈A~:~ x_1≠x_2→f(x_1)≠f(x_2)*
Equivalentemente:
*f \ \text{es inyectiva} ↔ ∀a∈A \ ∀b∈A : f(a)=f(b)→a=b*
Geométricamente, si una función es inyectiva, una recta horizontal corta a la gráfica a lo sumo en un punto. Si esto no ocurre, significa que la función toma el mismo valor de y para al menos dos valores del dominio, con lo cual la función no es inyectiva.
Prueba de la recta horizontal: una función es inyectiva sí y solo sí no existe una recta horizontal que cruce su gráfica más de una vez.
La función cuadrática *f(x)=x^2* no es inyectiva pues, si observamos su gráfica, infinitas rectas horizontales pueden cortarla más de una vez, o sea, existen valores distintos del dominio que tienen la misma imagen. Por ejemplo *x=-2* y *x=2*, ya que *f(-2)=f(2)=4.*
En cambio, la función cúbica *g(x)=x^3* sí es inyectiva, pues ninguna recta horizontal corta la gráfica más de una vez.
Otro ejemplo es la función lineal *h(x)=2x+1,* la cual es inyectiva porque supera la prueba de la recta horizontal.
Si tenemos una función no inyectiva, en algunos casos es posible realizar una restricción del dominio para que se convierta en inyectiva. Con la misma regla de definición, recortamos el dominio para que no existan valores distintos con la misma imagen.
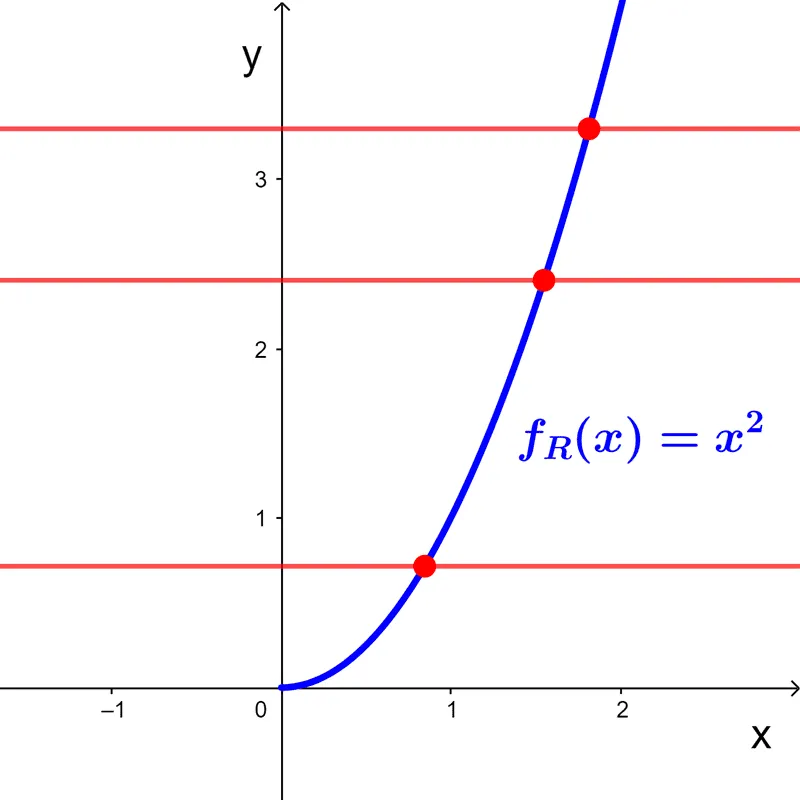
Por ejemplo, en *f(x)=x^2* podríamos quitar a los números negativos del dominio, de tal forma que tendríamos una función restringida *f_R=x^2* donde *D_R=[0,+∞)*. Esta función no es igual a la original, pues tiene un dominio distinto, pero en el intervalo indicado ambas funciones dan los mismos valores. Si miramos la gráfica de la función restringida veremos que ahora sí es inyectiva:
A la hora de restringir, comúnmente buscamos realizar la mínima restricción posible para que la función se convierta en inyectiva conservando la mayor cantidad de imágenes.
Otros ejemplos de funciones inyectivas son:
- *y=\sqrt{x}*
- *y=\ln x*
- *y=4x^3+2x+3*
- *y=e^x*
Función sobreyectiva
Una función f es sobreyectiva si su rango coincide con su codominio. Si llamamos A a su dominio y B a su codominio, entonces:
*f~~\text{es sobreyectiva} ↔ ∀y∈B, ∃x∈A~:~y=f(x)*
Es decir: todo elemento del codominio es imagen de algún elemento del dominio.
Cuando tenemos la fórmula de una función, solemos considerar como codominio al conjunto de los números reales. Por ello, la función cuadrática *f(x)=x^2* tiene dominio *\mathbb{R}* y codominio *\mathbb{R}*. Deducimos rápidamente que su rango es *[0,+∞),* porque un número elevado al cuadrado siempre es no negativo. Como *\mathbb{R}≠[0,+∞)*, la función no es sobreyectiva.
La función *g(x)=x^3* tiene dominio *\mathbb{R}*, codominio *\mathbb{R}* y su rango es *\mathbb{R}.* Como ocurre que codominio y rango coinciden, la función sí es sobreyectiva.
Podemos aplicar un procedimiento para que una función se convierta en sobreyectiva si no lo es. En este caso, lo que haremos es restringir el codominio de modo que sea igual al rango. Por ejemplo, en base a *f(x)=x^2*, creamos una nueva función cuyo codominio sea *[0,+∞)* de tal modo que coincida con el rango. Esta nueva función *f_R=x^2* donde *Cod_R=[0,+∞)* sí es sobreyectiva.
Otros ejemplos de funciones sobreyectivas son:
- *y=\ln x*
- *y=3x^3+5*
- *y=-6x+4*
- *y=\cos x* (si restringimos su codominio a *[-1,1]*)
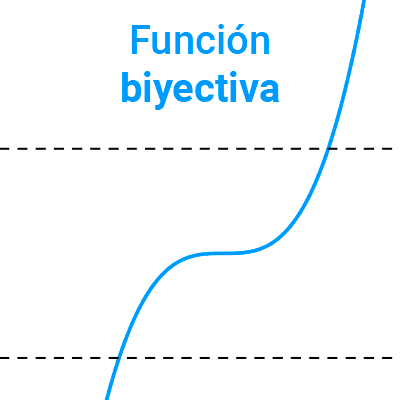
Función biyectiva
Una función es biyectiva si es inyectiva y sobreyectiva a la vez. En este caso queda establecida una correspondencia biunívoca entre los elementos del dominio y el codominio donde cada elemento del dominio corresponde a un único elemento del codominio y viceversa.
Para comprobar la biyectividad debemos comprobar primero si la función es inyectiva y sobreyectiva. En el caso de que no se cumpla, podemos recurrir a los procedimientos de restricción antes explicados para lograrlo.
Por ejemplo, *g(x)=x^3* es una función biyectiva, pues antes probamos que es tanto inyectiva como sobreyectiva.
La función *f(x)=x^2* no cumple ninguna de las dos condiciones, pero realizando la restricción de dominio y codominio de modo que estos sean igual a *[0, +∞)*, se convierte en una función biyectiva.
La importancia de las funciones biyectivas reside en que sus relaciones inversas también son funciones biyectivas. Esto es porque, al haber una correspondencia de uno a uno, podríamos invertir la relación y entonces a cada elemento del codominio correspondería uno del dominio, cumpliendo así con la definición de función. En conclusión, toda función biyectiva tiene función inversa.
Otros ejemplos de funciones biyectivas son:
- *y=2x-3*
- *y=-5x^3+4*
- *y=\ln x*
- *y=\sqrt {x}* (solo si restringimos su codominio a *[0, +∞)*)
Bibliografía
- Edwards, C. y Penney, D. (1997). Cálculo Diferencial e Integral (4ta edición). Pearson Educación.
- Larson, R. y Edwards, B. (2010). Cálculo 1 de una variable (9na edición). McGraw Hill.
- Leithold, L. (1998). El Cálculo (7ma edición). Oxford University Press.
- Piskunov, N. (1977). Cálculo diferencial e integral (3ra edición). Editorial Mir Moscú.
- Rabuffetti, H. (1999). Introducción al Análisis Matemático: Cálculo 1 (15a edición). El Ateneo.
- Sadosky, M. y Guber, R. (1984). Elementos de cálculo diferencial e integral (17a edición). Librería y Editorial Alsina.
- Stewart, J. (2012). Cálculo de una variable, trascendentes tempranas (7ma edición). Cengage Learning.
- Thomas, G. (2006). Cálculo, una variable (11a edición). Pearson Educación.
- Zill, D. y Wright, W. (2011). Cálculo, trascendentes tempranas (4ta edición). McGraw Hill.








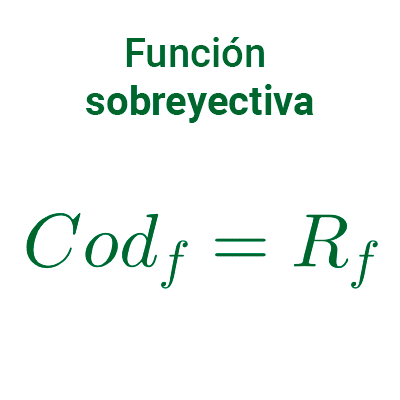
Deja una respuesta