Función inversa
En este artículo explicamos qué es una función inversa pasando por su concepto y definición, cuáles son las condiciones necesarias para que exista y las propiedades algebraicas y geométricas que cumplen junto con ejemplos.
Índice
¿Qué es una función inversa?
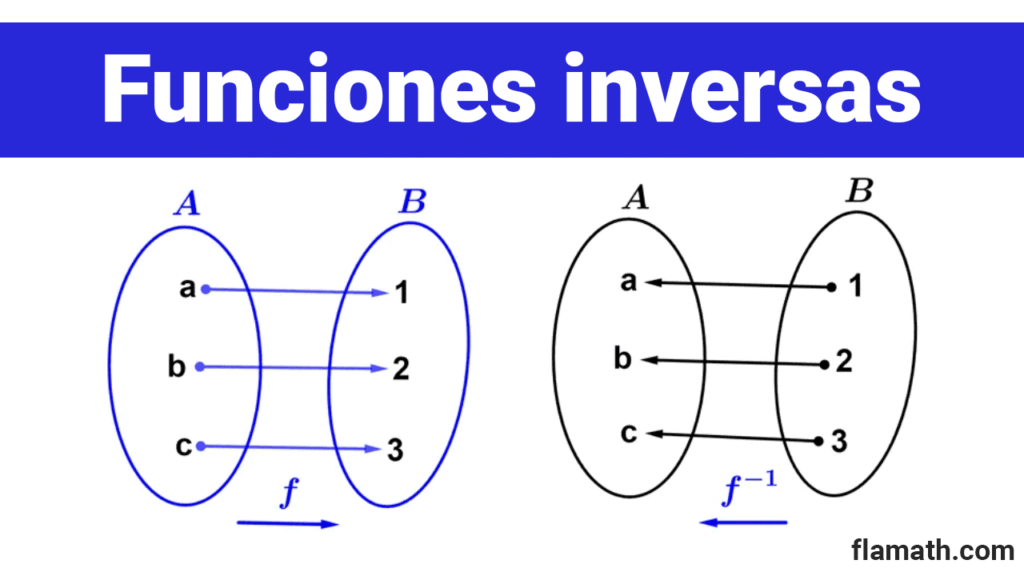
Una función inversa es una función que deshace el efecto de otra función. En otras palabras, si la función original transforma un elemento a es un elemento b, la función inversa transforma al elemento b en el elemento a, es decir, lo devuelve al estado original. La inversa de una función f(x) se simboliza como f-1(x), con el superíndice "-1".
Por ejemplo, si consideramos la función *f(x)=2x,* esta función toma a un número x y lo multiplica por dos; su función inversa deberá tomar al resultado y devolver al número x, esto se consigue dividiendo entre dos, entonces la inversa de *f* es *f^{-1}(x)=\frac{x}{2}.* En particular, si *x=2,* entonces *f(x)=4,* y si introducimos *4* en *f^{-1}(x),* nos queda *f^{-1}(4)=2,* que es el número con el que comenzamos.
¿Cuándo una función tiene inversa?
No todas las funciones tienen inversa. Para que una función tenga una inversa, debe ser biyectiva (uno a uno), esto significa que cada elemento del dominio tiene exactamente un elemento correspondiente en el codominio y que todos los elementos del codominio tienen al menos un elemento correspondiente en el dominio.
Consideremos a la función cuadrática *f(x)=x^2.* Esta función recibe como entrada al número x y devuelve su cuadrado. El trabajo de una inversa sería entonces tomar a ese cuadrado y devolvernos el número original x. Por ejemplo, para x=2, f(2)=4. La inversa debería tomar ese 4 y regresarnos al 2. Pero hay un problema, pues también para x=-2, f(-2)=4. Es decir, tanto 2 como -2 tienen de imagen al número 4.
No puede haber una función inversa en este caso, porque debería devolver dos valores distintos si introducimos al número 4, no cumpliendo la condición de unicidad de una función. Entonces, la función *f(x)=x^2*, bajo estas condiciones, no tiene inversa, porque no es biyectiva.
Ahora bien, si consideramos otro caso, como la función lineal *g(x)=2x+1,* las cosas cambian. Por ejemplo, para x=5, g(5)=11 y no existe otro valor del dominio que arroje de imagen al número 11. Entonces, sí existe una función inversa, la cual en este caso tomará al 11 y devolverá 5. Esto fue posible porque no existen números diferentes del dominio que tengan la misma imagen, en otras palabras, la función es biyectiva.
Definición formal
En base al razonamiento anterior podemos pasar del concepto para definir formalmente a una función inversa, explicitando las condiciones que se deben cumplir para que exista.
Definición: Sea f una función biyectiva con dominio A y rango B. Entonces su función inversa f-1 tiene dominio B y rango A y está definida por:
*f^{-1}(y)=x~* si y solo si *~f(x)=y~* para toda *y* en B.
La definición no dice nada distinto a lo que venimos haciendo. Si f toma una x, la transforma y devuelve una y, entonces la inversa f-1 tomará a esa y, la transformará y devolverá x; lo mismo ocurre en sentido contrario. Lo fundamental es que f debe ser una función biyectiva. Como vimos, este requisito es necesario para que, según cada valor de y, el valor de f-1(y) sea único.

Importante: *f^{-1}* es un símbolo para la función inversa de *f.* El *-1* usado no es un exponente. Es decir, *f^{-1}* no significa *\frac{1}{f(x)}.*
Una característica importante es que el dominio de la función original es el rango de la inversa, y el rango de la función inversa es igual al dominio de la función original. Así:
Dominio de *f* = Rango de *f^{-1}*
Rango de *f* = Dominio de *f^{-1}*
Realizando un pequeño trabajo de reemplazos, podemos llegar a las siguientes expresiones, conocidas como ecuaciones de cancelación, Si *f* y *f^{-1}* son funciones inversas, se verifica que:
*f^{-1}(f(x))=x~* para toda x en el dominio de f
*f(f^{-1}(x))=x~* para toda x en el rango de f
En otras palabras, la composición de una función con su inversa, o de una inversa con la original, da como resultado la función identidad. Podemos utilizar estas ecuaciones para comprobar que dos funciones son inversas. Por ejemplo, probaremos que *f(x)=2x* tiene como inversa a *f^{-1}(x)=\frac{x}{2}:*
*f^{-1}(f(x))=f^{-1}(2x)=\dfrac{2x}{2}=x*
*f(f^{-1}(x))=f \left(\dfrac{x}{2} \right)=2 \left(\dfrac{x}{2} \right)=x*
Existe un teorema que asegura que si una función creciente o decreciente en un intervalo, entonces es biyectiva y tiene inversa en ese intervalo. En efecto, si *f* es creciente en el intervalo I, satisface la desigualdad *f(x_2)>f(x_1)* cuando *x_2>x_1,* lo cual asegura que no habrá imágenes iguales; entonces, f es biyectiva y tiene una inversa. Lo mismo ocurre con las funciones decrecientes.
Las funciones que no son crecientes ni decrecientes aún pueden ser biyectivas y tener una inversa, como la función *f(x)=\frac{1}{x}* para *x≠0* y *f(0)=0,* definida en *\mathbb{R}.*
Gráficas de funciones inversas
La gráfica de función y su inversa son simétricas respecto a la recta y=x. Entonces, se puede obtener una a partir de la otra realizando la reflexión.
Esto se debe a que, como *f(a)=b* si y solo si *f^{-1}(b)=a,* el punto *(a,b)* está en la gráfica de *f* si y solo si el punto *(b,a)* está en la gráfica de *f^{-1}.* Pero, obtenemos el punto *(b,a)* a partir de *(a,b)* al reflejar respecto a la recta de ecuación *y=x.* También, los puntos de intersección de una función con los ejes x e y son los mismos que los de su función inversa, pero intercambiados.
Propiedades
Resumimos a continuación las características de funciones inversas.
- Una función tiene inversa solo si es biyectiva, y esta inversa es otra función biyectiva.
- Si una función creciente o decreciente en un intervalo, entonces tiene inversa en ese intervalo.
- El dominio de una función es el rango de su inversa, y el rango de la inversa es igual al dominio de la función original.
- Las gráficas de dos funciones inversas son simétricas respecto a la recta y=x.
- Los puntos de intersección de una función con los ejes x e y son los mismos que los de su función inversa, pero intercambiados.
- La composición de una función con su inversa, o de una inversa con la original, da como resultado la función identidad.
- La función inversa de una función inversa es igual a la función original. En símbolos: *(f^{-1})^{-1}=f*
Ejemplos
Habiendo comprobado que una función es biyectiva, para calcular su inversa debemos seguir los siguientes pasos:
- Escribir y=f(x).
- Despejar x de esta ecuación en términos de y (si es posible).
- Expresar f-1 como una función de x, intercambiando x e y. La ecuación resultante es y=f-1(x).
A continuación, veremos algunos ejemplos de funciones conocidas y sus inversas. Pueden seguirse los pasos anteriores para confirmar los resultados.
Funciones lineales
Todas las funciones lineales que no constantes son biyectivas y tienen inversa. Una función *f(x)=ax+b* donde *a* y *b* son números reales y *a\neq 0* tiene como inversa a la función
*f^{-1}(x)=\dfrac{x-b}{a}*
Las funciones constantes de la forma *f(x)=b* no tienen inversa porque no son biyectivas.
Ejemplo: la inversa de la función lineal *f(x)=-3x-4* es *f^{-1}(x)=-\dfrac{x+4}{3}*
Funciones cuadráticas
Como vimos anteriormente, la función cuadrática *y=x^2* no es biyectiva, por tanto, no tiene inversa. Sin embargo, si consideramos un subconjunto de su dominio donde sí cumple esa condición, podemos hallar una inversa. Este mismo principio se aplica para todas las funciones cuadráticas.
Ejemplo: dada la función *f(x)=x^2+1,* si tomamos como dominio a los reales no negativos *(x≥0),* la inversa existe y es *f^{-1}(x)=\sqrt{x-1}.* Entonces, la inversa de esta función cuadrática es una función raíz cuadrada.
Nota: si en lugar de restringir el dominio a los números no negativos decidiésemos hacerlo a los no positivos *(x≤0),* para conservar la congruencia, en el despeje de la inversa debemos tomar la raíz cuadrada negativa, de modo que el dominio de la función original coincida con el rango de la inversa. Entonces, para *f(x)=x^2+1,* donde *x≤0,* la función inversa es *f^{-1}(x)=-\sqrt{x-1}*
Funciones cúbicas
Las funciones cúbicas donde no hay término cuadrático ni lineal son biyectivas, por tanto, podemos hallar una inversa. Introducir dichos términos puede provocar que se pierda la biyectividad.
Ejemplo: *f(x)=2x^3+1* tiene como inversa a *f^{-1}(x)=\sqrt[3]{\dfrac{x-1}{2}},* es decir, la inversa de una función cúbica involucra una función raíz cúbica.
Funciones radicales
Las funciones radicales son aquellas en las que la variable independiente aparece dentro de una raíz cuadrada, cúbica o de otro índice. Es necesario comprobar en cada caso la biyectividad y si se pueden realizar los despejes para obtener la inversa.
Ejemplo 1: la función *f(x)=\sqrt[3]{1+2x}* es biyectiva y su inversa es *f^{-1}(x)=\dfrac{x^3-1}{2}*
Ejemplo 2: la función *g(x)=\sqrt{x-3}* es biyectiva y su inversa es *g^{-1}(x)=x^2+3.* Es importante destacar que el rango de *g* es *[0,+∞),* en cambio, el dominio de *g^{-1},* si no especificamos nada, es *\mathbb{R}.* Para evitar esta incongruencia y hacer que se cumpla la propiedad que viene con la definición, debemos restringir el dominio de *g^{-1}* a *[0,+∞)*.
Finalmente, la inversa de *g* es *g^{-1}(x)=x^2+3* con *D_{g^{-1}}=[0,+∞)*
Funciones racionales
En las funciones racionales será necesario primero comprobar la biyectividad. Existen algunas de ellas en las que sí se cumplen esta condición.
Ejemplo: la función racional *f(x)=\dfrac{1}{x+2}* es biyectiva y su inversa es *f^{-1}(x)=\dfrac{1}{x}-2.*
Funciones exponenciales y logarítmicas
Las funciones exponenciales y logarítmicas están estrechamente relacionadas y son inversas una de la otra. Una función exponencial *f(x)=a^x* donde a es positivo y distinto de 1 tiene como inversa a la función logarítmica *f^{-1}(x)=\log_a{x}.* Algunos casos particulares son:
- La función exponencial natural *f(x)=e^x* es la inversa de la función logaritmo natural *f^{-1}(x)=\ln{x}.*
- La función exponencial decimal (con base 10) *f(x)=10^x* es la inversa de la función logaritmo decimal *f^{-1}(x)=\log{x}.*
Funciones trigonométricas
Las funciones trigonométricas no son biyectivas en sus dominios naturales, sin embargo, podemos realizar restricciones convenientes para que estas funciones tengan una inversa. De este modo, las funciones seno, coseno y tangente tienen como inversas a las funciones arcoseno, arcocoseno y arcotangente, respectivamente.
En el siguiente cuadro se muestran cada función con su inversa y el dominio y rango de esta última.
| Función trigonométrica | Función inversa | Dominio de la inversa | Rango de la inversa |
|---|---|---|---|
| *\sin(x)* | *\arcsin(x)* | *[-1, 1]* | *[-\frac{π}{2}; \frac{π}{2}]* |
| *\cos(x)* | *\arccos(x)* | *[-1, 1]* | *[0, π]* |
| *\tan(x)* | *\arctan(x)* | *(-∞, +∞)* | *(-\frac{π}{2}; \frac{π}{2})* |
Bibliografía
- Edwards, C. y Penney, D. (1997). Cálculo Diferencial e Integral (4ta edición). Pearson Educación.
- Larson, R. y Edwards, B. (2010). Cálculo 1 de una variable (9na edición). McGraw Hill.
- Leithold, L. (1998). El Cálculo (7ma edición). Oxford University Press.
- Piskunov, N. (1977). Cálculo diferencial e integral (3ra edición). Editorial Mir Moscú.
- Rabuffetti, H. (1999). Introducción al Análisis Matemático: Cálculo 1 (15a edición). El Ateneo.
- Sadosky, M. y Guber, R. (1984). Elementos de cálculo diferencial e integral (17a edición). Librería y Editorial Alsina.
- Stewart, J. (2012). Cálculo de una variable, trascendentes tempranas (7ma edición). Cengage Learning.
- Thomas, G. (2006). Cálculo, una variable (11a edición). Pearson Educación.
- Zill, D. y Wright, W. (2011). Cálculo, trascendentes tempranas (4ta edición). McGraw Hill.

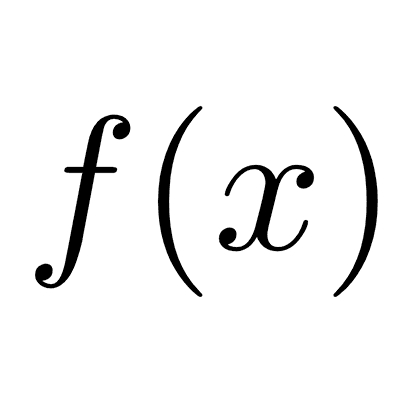











Deja una respuesta