
Símbolos lógicos
En este artículo explicamos cuáles son los símbolos lógicos más utilizados en lógica simbólica, sus significados y ejemplos de utilización.
Índice
¿Qué son los símbolos lógicos?
En lógica matemática, los símbolos lógicos son herramientas fundamentales para expresar ideas y relaciones complejas de manera precisa e inequívoca. Estos símbolos, a diferencia del lenguaje natural que puede ser ambiguo, poseen un significado universalmente aceptado, lo que permite formular proposiciones, argumentos y demostraciones con rigor y claridad.
Las principales funciones de los símbolos lógicos son:
- Representar proposiciones: los símbolos lógicos permiten simbolizar enunciados que pueden ser verdaderos o falsos.
- Establecer relaciones entre proposiciones: los conectivos lógicos permiten conectar proposiciones simples para formar proposiciones compuestas más complejas.
- Cuantificar el alcance de las proposiciones: los cuantificadores permiten indicar la cantidad de elementos de un conjunto para los cuáles es válida una proposición.
- Estructurar argumentos lógicos: los símbolos lógicos se utilizan para construir argumentos válidos, es decir, conjuntos de proposiciones que conducen a una conclusión lógica.
- Formalizar demostraciones matemáticas: los símbolos lógicos son esenciales para formular demostraciones matemáticas precisas que, utilizando axiomas y reglas de inferencia, permiten establecer la veracidad de los teoremas matemáticos.
Lista de los símbolos lógicos
Proposiciones o variables
Las proposiciones son enunciados que pueden ser verdaderos o falsos. Se simbolizan con las letras p, q, r, s, etc. Por ejemplo:
- p: “Está lloviendo”.
- q: “El techo está mojado”.
La verdad se indica con la letra V y la falsedad con la letra F. El valor de verdad de una proposición p se indica como v(p).
Conectivos lógicos
Los conectivos lógicos, también conocidos como operadores lógicos, son símbolos que se utilizan para conectar dos o más proposiciones con el fin de formar proposiciones más complejas. Existen seis conectores lógicos:
- Negación (¬): representa falsedad de una proposición y se lee como "no" o "es falso que". Ejemplo: si p es “está lloviendo”, ¬p es “no está lloviendo”.
- Conjunción (∧): indica la unión de dos o más proposiciones que deben ser ciertas simultáneamente para que la expresión completa sea verdadera. Se lee como "y" o “pero”. Ejemplo: p es “está lloviendo” y q es “el techo está mojado”, la proposición p∧q es “está lloviendo y el techo está mojado”.
- Disyunción (∨): representa la alternativa entre dos o más proposiciones. Al menos una de ellas debe ser cierta para que la expresión completa sea verdadera. Se lee como "o". Ejemplo: si p es “está lloviendo” y q es “el techo está mojado, p∨q es “está lloviendo o el techo está mojado, o ambos”.
- Disyunción exclusiva (⊻): representa la alternativa entre dos o más proposiciones pero sólo una de las dos puede ser cierta para que la expresión sea cierta. Se lee como “o … pero no ambos”. Ejemplo: si p es “está lloviendo” y q es “el techo está mojado“, p⊻q es “o está lloviendo o el techo está mojado, pero no ambos”.
- Condicional o implicación (→): establece una relación de causa-consecuencia entre dos proposiciones. La primera proposición (antecedente) implica la segunda (consecuente). Se lee como "si... entonces". Ejemplo: para p: “está lloviendo” y q: “el techo está mojado”, p→q es “si está lloviendo, entonces el techo está mojado”.
- Bicondicional o doble implicación (↔): expresa una equivalencia lógica entre dos proposiciones. Ambas proposiciones deben ser verdaderas o falsas al mismo tiempo. Se lee como "si y sólo si". Ejemplo: si p es “está lloviendo” y q es “el techo está mojado”, p↔q es “Está lloviendo si y sólo si el techo está mojado”.
Para agrupar proposiciones con conectivos se pueden usar paréntesis (), corchetes [] y llaves {}. Por ejemplo, p→(q∧r) es la implicación entre la proposición p y la proposición q∧r.
Cuantificadores
Los cuantificadores lógicos son símbolos que se utilizan para indicar la cantidad de elementos de un conjunto que satisfacen una determinada propiedad o predicado. Existen tres cuantificadores ampliamente utilizados:
- Cuantificador universal (∀): indica que una proposición es cierta para todos los elementos de un conjunto. Se lee como "para todo" o “para cada”. Ejemplo: ∀x ∈ R, x2 ≥ 0 (para todo número real x, se cumple que x al cuadrado es mayor o igual que 0).
- Cuantificador existencial (∃): indica que existe al menos un elemento en un conjunto para el que una proposición es cierta. Se lee como "existe" o "hay al menos uno". Ejemplo: ∃x ∈ R, x2=2 (existe un número real x que elevado al cuadrado es igual a 2).
- Cuantificador de existencia única (∃!): indica que existe un único elemento que cumple con la condición específica. Se lee como "existe un único" o "hay exactamente uno". Ejemplo: ∃! x ∈ R, x2=0 (existe un único número real que elevado al cuadrado es 0).
Otros símbolos
- Para el cuantificador universal suelen usarse los dos puntos “:” para separar la cuantificación del predicado y se leen como “se verifica”.
Ejemplo: ∀x ∈ R: x2 ≥ 0 (para todo número real x, se verifica que x al cuadrado es mayor o igual que 0). - Para los cuantificadores existenciales se suele usar el símbolo “/” que se lee como “tal que”.
Ejemplo: ∃x ∈ R / x2=2 (existe un número real x tal que x al cuadrado es igual a 2). - También es usado habitualmente el símbolo ∴ (por lo tanto) para indicar una conclusión.
Ejemplo: x∈R ∧ y∈R, ∴ xy∈R (x e y son números reales, por lo tanto el producto xy es un número real).
Tabla de los símbolos lógicos
En la siguiente tabla se resumen los símbolos de lógica más usados junto con su nombre y forma de leerse.
| Símbolo | Nombre | Se lee |
|---|---|---|
| ¬ | Negación | no |
| ∧ | Conjunción | y |
| ∨ | Disyunción | o |
| ⊻ | Disyunción exclusiva | o (pero no ambos) |
| → | Condicional | si… entonces |
| ↔ | Bicondicional | si y sólo si |
| ∀ | Cuantificador universal | para todo |
| ∃ | Cuantificador existencial | existe al menos un |
| ∃! | Cuantificador de existencia única | existe solo un |
DESCARGAR TABLA DE SÍMBOLOS LÓGICOS EN PDF
Bibliografía
- Acevedo González, G. (2011). Lógica Matemática. Universidad Nacional Abierta y a Distancia (UNAD).
- Castillo P, E. y Pinta, M. (2015). Lógica Matemática I: Proposiciones y Leyes de Inferencia (2da edición). Universidad Técnica de Machala.
- Copi, I. y Cohen, C. (2013). Introducción a la Lógica (2da edición). Limusa.
- Corral de Franco, Y. y Manzanares, L. (2018). Nociones Elementales de lógica matemática y teoría de conjuntos. Caracas. Fondo editorial OPSU.
- Daun, J. y Falcón, Y. (1995). Lógica matemática. Universidad Autónoma Metropolitana.
- Garrido, M. (1974). Lógica simbólica (4ta edición). Tecnos.
- Gentile, E. (1984). Notas de Álgebra I. Editorial Universitaria de Buenos Aires.
- Moreno, A. (1969). Lógica matemática: antecedentes y fundamentos. Editorial Universitaria de Buenos Aires.
- Puyau, H. y Roetti, J. (1976). Elementos de Lógica Matemática. Editorial Universitaria de Buenos Aires.
- Rojo, A. (1996). Álgebra I (18a edición). El Ateneo.


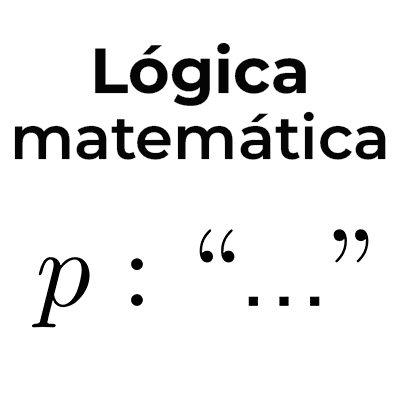
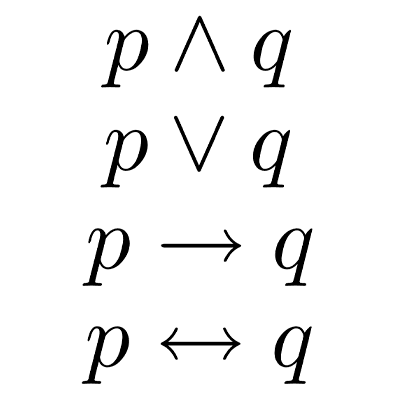
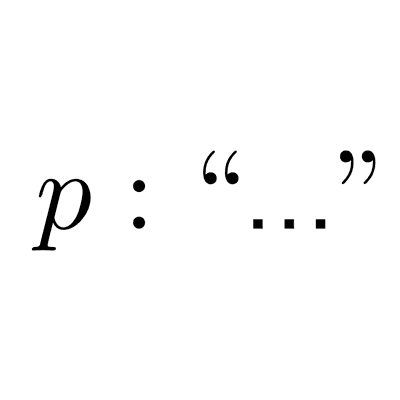
Deja una respuesta