Dominio de una función

En este artículo explicamos qué es el dominio de una función, cómo se interpreta gráficamente y ejemplos de dominios de funciones habituales.

¿Qué es el dominio?

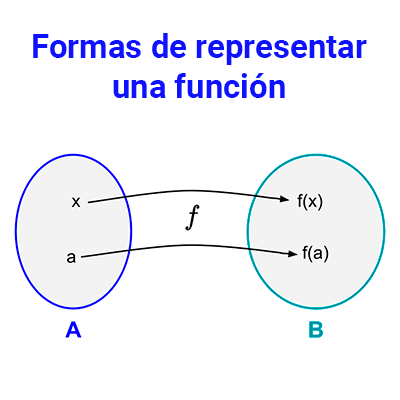
El dominio de una función es el conjunto de valores que puede tomar la variable independiente, es decir, aquellos para los cuales existe imagen. El dominio también recibe el nombre de campo de existencia o conjunto de partida. Se simboliza con una letra D y en ocasiones con el nombre de la función como subíndice. 

En funciones reales, el dominio es un subconjunto de los números reales. Así, el dominio de una función real f se define simbólicamente como:

*D_f=\{x∈\mathbb{R}~|~∃y∈\mathbb{R}~∧~y=f(x)\}*

Recordemos que una función es una regla que asigna a todo elemento de un conjunto A un único elemento de un conjunto B. El conjunto A es al que llamamos dominio de la función, el conjunto B es el codominio, el rango es un subconjunto de B.

Los dominios de funciones reales suelen expresarse como intervalos, uniones de intervalos o restas de conjuntos. Los intervalos pueden ser abiertos, cerrados, semiabiertos, finitos o infinitos. 

Una función puede venir dada junto con su dominio explícito, por ejemplo, para la función *f(x)=2x+3* donde *0≤x<6,* su dominio es el intervalo *[0,6),* porque x solo puede estar entre esos valores. Si el dominio no viene explícito y la función está dada por una ecuación, se considerará como dominio al conjunto más grande de números reales en el es posible realizar las operaciones que aparecen en la fórmula. Este es llamado el dominio natural.

Para la función *g(x)=1/x,* es posible realizar la operación para todos los números reales excepto el cero, pues si hacemos *x=0,* se produce la expresión *1/0,* la cual no es un número. Entonces, el dominio natural de g es *D_g=R-\{0\}.* Escribiendo como una unión de intervalos, el dominio es *D_g=(-∞,0)∪(0,+∞).*

La función *y=\sqrt{x}* toma a un número real x y devuelve su raíz cuadrada. Como no es posible sacar la raíz cuadrada de un número negativo en el campo de los números reales, el dominio de f son todos los números reales no negativos, es decir, *x≥0* o el intervalo *[0, +∞).*

El dominio de una función se puede determinar a partir de su gráfica proyectándola sobre el eje horizontal (eje x). El intervalo que abarque sobre este eje será el dominio.

Se puede restringir el dominio de una función según el contexto. Por ejemplo, el área de un círculo está dada por la función *A=πr^2,* donde *r* es el radio del círculo. Como solo nos interesan valores de *r* positivos (porque son distancias), el dominio queda restringido a *r>0,* o el intervalo *(0, +∞).*

También podemos restringir dominios cuando lo creamos conveniente, siempre que lo indiquemos adecuadamente. El dominio de *y=x^2+7* es el conjunto completo de los números reales. Si deseamos restringirlo a, por ejemplo, solo los valores de x mayores a 4, debemos escribir *y=x^2+7,* *x>4.*

Dominios de las operaciones con funciones

Si dos funciones f y g tienen dominios *D_f* y *D_g* respectivamente, entonces la suma, resta, multiplicación y división de estas funciones tiene como dominio al conjunto de valores compartidos por los dominios originales. Del dominio de la división se excluyen aquellos valores que hacen cero al denominador.

*D_{f+g}=D_f ∩ D_g*

*D_{f-g}=D_f ∩ D_g*

*D_{f\cdot g}=D_f ∩ D_g*

*D_{f/g}=D_f ∩ D_g - \{x~|~g(x)=0\}*

Dominios de funciones conocidas

En general, para encontrar el dominio de una función, hay que tener en cuenta cualquier restricción que pueda haber debido a las operaciones matemáticas que definen la función. Algunas restricciones comunes incluyen:

• No se puede dividir por cero.
• No se puede tomar raíces cuadradas (o de cualquier índice par) de números negativos en el conjunto de los números reales.
• No se pueden calcular logaritmos de números no positivos.

Funciones polinómicas 

Las funciones polinómicas son aquellas de la forma *f(x)=a_0+a_1x+a_2x^2+a_3x^3+…+a_nx^n* donde los *a_0,* *a_1,a_2,...,a_n* son números reales llamados coeficientes. El dominio de toda función polinómica es el conjunto de los números reales, porque no existen restricciones para las operaciones. Es decir, las funciones lineales, cuadráticas, cúbicas o de cualquier grado tienen como dominio a los números reales.

Ejemplos

• El dominio de la función lineal *y=-3x+5* es *\mathbb{R}.*
• El dominio de la función cuadrática *f(x)=x^2+4x+5* es *\mathbb{R}.*
• El dominio de la función cúbica *y=-x^3+2x+4* es *\mathbb{R}.*

Funciones racionales

Las funciones racionales son cocientes de funciones polinómicas. El dominio de toda función racional es el conjunto de los números reales exceptuando aquellos que hacen cero al denominador.

Ejemplos

• El dominio de la función *f(x)=\dfrac{1}{x+1}* es *D_f=\{x~ |~ x+1\neq 0\}=\mathbb{R}-\{-1\}.* Expresado en notación de intervalos, el dominio es *D_f=(-∞,-1)∪(-1,+∞).*
• Para la función *g(x)=\dfrac{x}{x^2-9},* como debe ocurrir que *x^2-9\neq 0,* el dominio es *D_g=\mathbb{R}-\{-3,3\}.* Como intervalo: *D_g=(-∞,-3)∪(-3,3)∪(3,+∞).*

Funciones radicales

Ejemplos

• Para *y=\sqrt{x+1},* el término *x+1* no puede ser negativo, o sea, debe pasar que *x+1≥0,* despejando se obtiene que *x≥-1.* El dominio es entonces *[-1,+∞).*
• En la función *y=\sqrt{1-x^2},* el radicando *1-x^2* debe ser no negativo, es decir, *1-x^2≥0,* despejando obtenemos *1≥x^2,* o *-1≤x≤1.* Entonces, el dominio es *[-1,1].* 
• Para *y=\sqrt[3]{x^2+\frac{2}{x}}* no existen restricciones con el radical, pues el índice es impar, sin embargo, en el radicando x está en un denominador y no puede ser cero, entonces el dominio es *\mathbb{R}-\{0\}.*

Funciones logarítmicas

Las funciones logarítmicas de cualquier base tienen como dominio al conjunto de números reales que hacen positivo a su argumento.

Ejemplos

• Para *y=\log(x),* el dominio son todos los reales tales que *x>0,* es decir, el intervalo *(0,+∞).*
• En *y=\ln(x-7),* el argumento *x-7* debe ser positivo, o sea, *x-7>0* que equivale a *x>7.* El dominio es entonces *(7,+∞).*
• La función *y=\log_2(x^2-9)* no puede tener argumento negativo, o sea que *x^2-9>0.* Despejando se obtiene que *x<-3* o *x>3.* El dominio es entonces *(-∞,-3)∪(3,+∞).*

Funciones exponenciales

El dominio de las funciones exponenciales es el conjunto de todos los números reales, salvo que en la expresión exista alguna operación restringida.

Ejemplos

• La función exponencial natural *y=e^x* no tiene restricciones de operaciones, entonces su dominio son todos los números reales.
• En *y=e^{1/x},* como x está en un denominador, no puede ser cero. Salvo esa excepción, todos los números reales tienen imagen. Entonces el dominio es *\mathbb{R}-\{0\}.*
• Para la función *y=3^{\sqrt{x}},* la variable independiente está dentro de una raíz cuadrada, con lo cual debe ser no negativa. Por lo tanto, el dominio de la función es *[0,+∞).*

Funciones trigonométricas

Los dominios de las funciones trigonométricas se expresan en la siguiente tabla.

Función	Dominio
Seno	*\mathbb{R}*
Coseno	*\mathbb{R}*
Tangente	*\mathbb{R}-\frac{n\pi}{2}* con n entero impar
Cosecante	*\mathbb{R}-n\pi* con n entero
Secante	*\mathbb{R}-\frac{n\pi}{2}* con n entero impar
Cotangente	*\mathbb{R}-n\pi* con n entero

Funciones hiperbólicas

Los dominios de las funciones hiperbólicas se expresan en la siguiente tabla.

Función	Dominio
Seno hiperbólico	*\mathbb{R}*
Coseno hiperbólico	*\mathbb{R}*
Tangente hiperbólica	*\mathbb{R}*
Cosecante hiperbólica	*\mathbb{R}-\{0\}*
Secante hiperbólica	*\mathbb{R}*
Cotangente hiperbólica	*\mathbb{R}-\{0\}*

Preguntas frecuentes

¡Continúa leyendo estos artículos relacionados!

Infografías