
Cómo calcular logaritmos
En este artículo explicamos cómo calcular logaritmos en calculadora y algunas técnicas para hacerlo sin necesidad de calculadora.
Índice
Calcular logaritmos en calculadora
Las calculadoras científicas permiten calcular logaritmos decimales (base 10) y logaritmos naturales (base e). Algunas calculadoras modernas permiten también resolver logaritmos de cualquier base, sin embargo, si no se dispone de una de ellas, igual es posible obtener logaritmos sin importar su base usando la propiedad del cambio de base de logaritmos.
Pasos para calcular logaritmos decimales y naturales
- Pulsar el botón “log” (para logaritmos decimales) o “ln” (para logaritmos naturales, base e).
- Ingresar el número del cual se quiere calcular el logaritmo y luego presionar "igual". La calculadora dará el resultado.
Nota: los logaritmos decimales son aquellos que se escriben como “log10” o simplemente “log” sin base. Los logaritmos naturales son llamados a veces como logaritmos neperianos.
Ejemplos
- Para calcular el logaritmo decimal de 100, en la calculadora escribimos “log 100”, el resultado será 2.
- Si queremos obtener el logaritmo natural de 5, en la calculadora escribimos “ln 5”, el resultado será aproximadamente 1,609437912.
Pasos para calcular logaritmos de cualquier base
- Pulsar la tecla “log” y escribir el número del cuál se quiere calcular el logaritmo. Luego, presionar el signo “igual”.
- Al resultado obtenido, dividirlo entre el logaritmo de la base, entonces se obtendrá logaritmo buscado.
Para calcular en un solo paso logc a, en la calculadora escribimos “(log a)÷(log c)” sin olvidar los paréntesis, pulsando “igual” se obtendrá el resultado. Si se quiere, en lugar de “log” se puede usar “ln”, pero es necesario usar el mismo en los dos pasos.
Ejemplos
- Para calcular log2 16, en la calculadora escribimos “log 16” y pulsamos igual. El resultado obtenido lo dividimos entre “log 2”, haciendo esto obtendremos que el resultado es 4. Es posible calcular en un solo paso escribiendo en la calculadora “(log 16)÷(log 2)”.
- Si buscamos calcular log7 343, en la calculadora escribimos “(log 343)÷(log 7)”, el resultado de esto será 3.
- Para calcular log5 300, en la calculadora colocamos “(log 300)÷(log 5)”, la calculadora arrojará el resultado 3,543959311.
Calcular logaritmos sin calculadora
Calcular logaritmos manualmente puede ser un desafío, pero es posible utilizando propiedades de los logaritmos, métodos de aproximación y series. Estos dos últimos son más complejos y requieren un conocimiento profundo de matemáticas, por tanto solo trataremos el uso de propiedades.
Casos conocidos
Los logaritmos decimales y naturales de potencias de 10 y e siempre darán por resultado la misma potencia. Para logaritmos de cualquier base: logb (bn)=n. En logaritmos decimales, cada cero que se agregue al argumento representa el aumento en una unidad del valor del logaritmo.
| Logaritmos decimales | Logaritmos naturales | Logaritmos binarios |
|---|---|---|
| log(1)=0 | ln(1)=0 | log2(1)=0 |
| log(10)=1 | ln(e)=1 | log2(2)=1 |
| log(100)=2 | ln(e2)=2 | log2(4)=2 |
| log(1000)=3 | ln(e3)=3 | log2(8)=3 |
| log(10000)=4 | ln(e4)=4 | log2(16)=4 |
| … | … | … |
Aplicación de propiedades
Conocer las propiedades de la logaritmación es útil para reescribir y simplificar expresiones que puedan parecer complicadas. Las propiedades más importantes son:
- Multiplicación: *\log_c (ab)=\log_c (a)+\log_c (b)*
- División: *\log_c (a/b)=\log_c (a)-\log_c (b)*
- Potencia: *\log_c (a^n)=n\cdot \log_c (a)*
- Raíz: *\log_c (\sqrt[n]{a^m})=\dfrac{m \log_c (a)}{n}*
- Cambio de base: *\log_c (a)=\dfrac{\log_b(a)}{\log_b(c)}*
Ejemplo 1
Obtener *\log(\sqrt[3]{10})*
Solución: puede parecer complicado obtener el logaritmo de una raíz cúbica sin una calculadora, sin embargo, podemos reescribir la raíz como un exponente fraccionario:
*\log(\sqrt[3]{10})=\log(10^{1/3})*
Ahora, usando la propiedad de la potencia, se la puede sacar del logaritmo. La expresión que queda es un logaritmo básico:
*\log(10^{1/3})=\dfrac{1}{3} \log (10)*
*=\dfrac{1}{3}*
Ejemplo 2
Calcular *\log (4)+\log (25)*
Solución: se tiene una suma de logaritmos de igual base, por tanto, esto puede escribirse como el logaritmo de un producto y luego resolver.
*\log (4)+\log (25)=\log(4\cdot 25)*
*=\log(100)*
*=2*
Ejemplo 3
Resolver *3\cdot (\log 5+\log 2)*
Solución: la expresión dentro del paréntesis puede escribirse como el logaritmo de un producto y luego resolverse.
*3\cdot (\log 5+\log 2)=3\cdot (\log(5\cdot 2))*
*=3\cdot (\log(10))*
*=3\cdot 1*
*=3*
Ejemplo 4
Calcular *\ln(4)+\ln(16)* sabiendo que *\ln(2)≈0,69.*
Solución: reescribiendo los argumentos como potencias de 2 se puede usar la propiedad de las potencias.
*\ln(4)+\ln(16)=\ln(2^2)+\ln(2^4)*
*=2\ln(2)+4\ln(2)*
*≈2\cdot 0,69+4\cdot 0,69*
*=1,38+2,76*
*=4,14*
Ejemplo 5
Calcular *\ln(0,1)* sabiendo que *\log (e)≈0,43.*
Solución: puede usarse la propiedad del cambio de base y la reescritura del argumento para obtener el valor buscado.
*\ln(0,1)=\dfrac{\log(0,1)}{\log(e)}*
*=\dfrac{\log(10^{-1})}{\log(e)}*
*≈\dfrac{-1}{0,43}*
*≈-2,3*
Ejemplo 6
Resolver *\log(25)* sabiendo que *\log(5)≈0,7*
Solución: reescribiendo el argumento y aplicando la propiedad del logaritmo de una potencia:
*\log(25)=\log(5^2)*
*=2\log(5)*
*≈2\cdot 0,7*
*=1,4*
Bibliografía
- Abálsamo, R., Berio, A., Mastucci, S., Quirós, N. y De Rossi, F. (2013). Matemática 5. Puerto de Palos.
- Leithold, L. (1994). Álgebra y Trigonometría con Geometría Analítica. Oxford University Press.
- Rojas Hincapié, C. (2022). Matemáticas de secundaria: grados 8-9. Fondo Editorial RED Descartes.
- Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.
- Zill, D. y Dewar, J. (2012). Álgebra, trigonometría y geometría analítica (3ra edición). McGraw Hill.


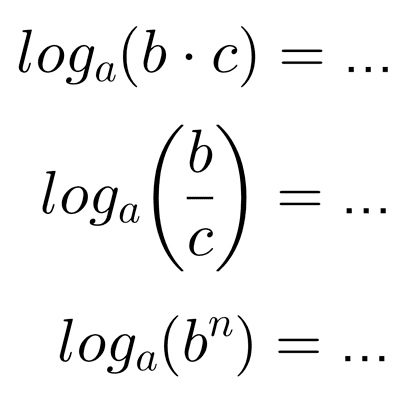
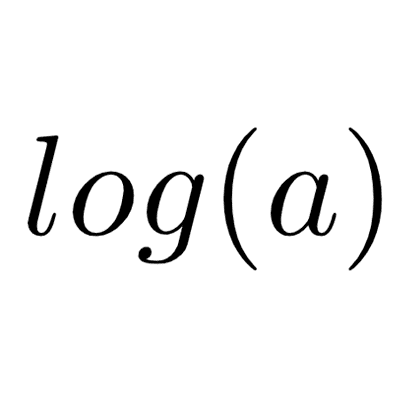

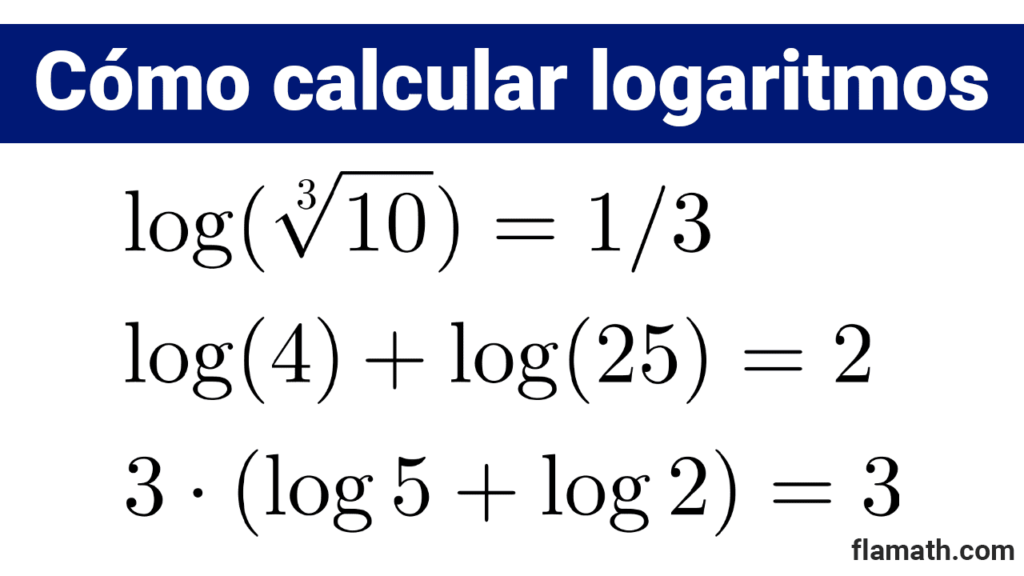
Deja una respuesta