
Logaritmos binarios (de base 2)
0 - Votos: 0
En este artículo explicamos qué son los logaritmos binarios o de base 2, vemos ejemplos de ellos y cómo obtenerlos usando cualquier calculadora científica.
Índice
¿Qué son los logaritmos binarios?
Los logaritmos binarios son aquellos que tienen base 2, es decir, el logaritmo binario de un número positivo a es el exponente al que se debe elevar 2 para obtener a y se simboliza como log2(a):
*\log_2(a)=b~~* si y solo si *~~2^b=a*
Ejemplos
A continuación, veremos algunos ejemplos de logaritmos binarios:
- El logaritmo en base 2 de 1 es 0, pues 20=1, esto se denota como: log2(1)=0.
- El logaritmo en base 2 de 8 es 3, porque 23=8, entonces log2(8)=3.
- El logaritmo en base 2 de 16 es 4, porque 24=16: log2(16)=4.
- El logaritmo en base 2 de 32 es 5, ya que 25=32, entonces log2(32)=5
- El logaritmo de base 2 de 64 es 6, pues 26=64, en notación de logaritmos: log2(64)=6.
- El logaritmo de 128 en base 2 es 7, porque 27=128, por tanto log2(128)=7.
- El logaritmo de 256 en base 2 es 8, pues 28=256, entonces log2(256)=8.
- El logaritmo binario de la raíz cuadrada de 2 es 1/2, pues 21/2=√2
Los logaritmos de base 2, como los de otras clases, pueden dar por resultados números negativos:
- log2(1/2)=-1 porque 2-1=1/2
- log2(1/4)=-2 porque 2-2=1/4
- log2(1/32)=-5 porque 2-5=1/32
También pueden dar como resultado números irracionales, es decir, con infinitas cifras decimales sin patrón. Esto ocurre cuando el argumento no es una potencia racional de 2:
- log2(3)=1,585…
- log2(π)=1,651…
- log2(10)=3,322…
Cómo calcular logaritmos de base 2
Las calculadoras científicas no tienen una función específica para obtener logaritmos binarios, sin embargo, es posible calcularlos igualmente usando la propiedad del cambio de base. De este modo, usando logaritmos decimales o naturales podemos hallar el valor de un logaritmo de base 2:
*\log_2 a=\dfrac{\log a}{\log 2}~~~~~\log_2 a=\dfrac{\ln a}{\ln 2}*
Pasos para calcular logaritmos binarios en una calculadora científica:
- Seleccionar la función log o ln y escribir el argumento (el número del cuál se quiere calcular el logaritmo) y presionar el signo igual.
- El resultado obtenido dividirlo entre log 2 o ln 2, dependiendo de cuál se usó al principio. Presionando el signo igual se obtendrá valor del logaritmo binario buscado.
Importante: si se usó log en el paso 1, se debe usar log en el paso 2, y lo mismo si se usó ln. Puede calcularse en una sola vez usando paréntesis adecuados. Por ejemplo, para calcular log2(16), lo que se debe escribir en la calculadora es: (log 16)÷(log 2) o (ln 16)÷(ln 2).
Aplicaciones
Los logaritmos binarios tienen varias aplicaciones prácticas en diversos campos, especialmente en informática, ciencias de la computación, teoría de la información y criptografía. Algunos ejemplos son:
- Análisis de algoritmos: se utilizan para calcular la eficiencia de algoritmos, determinando el número de pasos necesarios para completar una tarea.
- Criptografía: son usados para el diseño de algoritmos de cifrado para asegurar la confidencialidad de los datos.
- Compresión de datos: se emplean para reducir el tamaño de archivos de imagen, audio y vídeo.
- Codificación de datos: los logaritmos binarios se aplican para determinar el número de bits necesarios para representar un cierto rango de valores.
- Redes de computadoras: permiten calcular el ancho de banda, la capacidad de almacenamiento y otros parámetros importantes relacionados con la transmisión y recepción de datos.
Propiedades
Los logaritmos de base 2, al igual que los demás, cumplen las propiedades de los logaritmos:
- El logaritmo binario de uno es cero: log2(1)=0.
- El logaritmo binario de dos es uno: log2(2)=1.
- El logaritmo binario de una multiplicación es igual a la suma de los logaritmos binarios de los factores: log2(ab)=log2(a)+log2(b).
- El logaritmo binario de una división es igual a la resta de los logaritmos binarios del dividendo y divisor: log2(a/b)=log2(a) - log2(b).
- El logaritmo binario de una potencia es igual al exponente por el logaritmo binario de la base: log2(an)=n⋅log2(a).
- El logaritmo binario de una potencia de 2 es igual a la potencia: log2(2n)=n.
- El logaritmo binario de un número se puede obtener dividiendo el logaritmo del mismo número en otra base entre el logaritmo de 2 en esa nueva base: log2(a)=logc(a)÷logc(2).
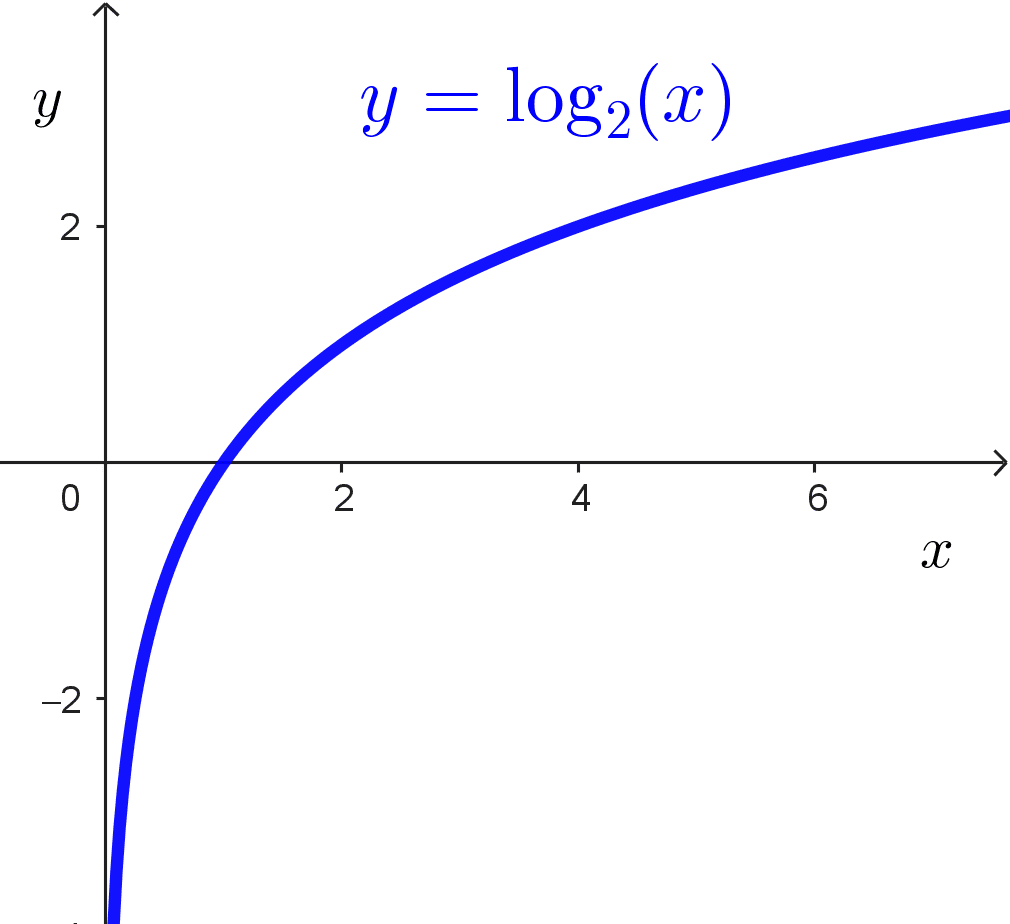
Función logaritmo binario
En Análisis Matemático podemos considerar al argumento de un logaritmo de base 2 como una variable independiente y obtener la función logaritmo binario *y=\log_2(x),* la cual es inversa de la función exponencial de base 2 *y=2^x.*
Bibliografía
- Abálsamo, R., Berio, A., Mastucci, S., Quirós, N. y De Rossi, F. (2013). Matemática 5. Puerto de Palos.
- Leithold, L. (1994). Álgebra y Trigonometría con Geometría Analítica. Oxford University Press.
- Rojas Hincapié, C. (2022). Matemáticas de secundaria: grados 8-9. Fondo Editorial RED Descartes.
- Sullivan, M. (2006). Álgebra y Trigonometría. Pearson Educación.
- Swokowski, E. y Cole, J. (2009). Álgebra y Trigonometría con Geometría Analítica. Cengage Learning.
- Zill, D. y Dewar, J. (2012). Álgebra, trigonometría y geometría analítica (3ra edición). McGraw Hill.
Subir



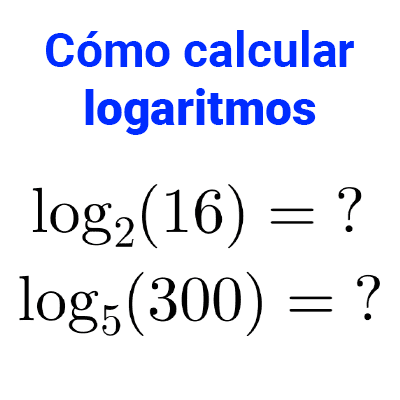


Deja una respuesta