Lógica matemática
0 - Votos: 0
En este artículo se estudian los conceptos fundamentales de la lógica que permitirán trabajar en áreas más avanzadas, como álgebra y cálculo, usando un lenguaje matemático claro.
Índice
¿Qué es la lógica matemática?
La lógica matemática es una disciplina que se centra en el estudio y la formalización del razonamiento y el pensamiento utilizando un conjunto específico de reglas y símbolos. Su principal objetivo es proporcionar un marco riguroso y preciso para expresar ideas, argumentos y relaciones en el ámbito de las matemáticas.
Cuando expresamos una idea en lenguaje natural, puede haber múltiples interpretaciones posibles. En matemáticas, como la precisión es esencial, una expresión ambigua o mal formulada puede llevar a conclusiones erróneas. La lógica matemática introduce un conjunto de símbolos y reglas formales que eliminan la ambigüedad y permiten expresar afirmaciones y relaciones de manera clara y precisa.
La simbología de la lógica matemática es universal, lo que facilita la comunicación entre matemáticos de diferentes culturas y permite que las ideas matemáticas sean accesibles para todos, independientemente de su idioma nativo.
En matemáticas es necesario demostrar la validez de afirmaciones y teoremas. La lógica proporciona reglas precisas para construir argumentos sólidos y demostraciones formales; esto asegura que las conclusiones sean correctas y confiables.
Tipos de lógica
Hay varios tipos de lógica matemática que se utilizan para modelar diferentes aspectos del razonamiento y la computación. Las más comunes son:
- Teoría de modelos: estudia la relación entre los símbolos de un sistema formal y los objetos que representan. Es decir, analiza cómo las estructuras matemáticas abstractas se pueden interpretar en el mundo real.
- Teoría de la demostración: se centra en las reglas y métodos para construir demostraciones formales de teoremas matemáticos. Investiga cómo se pueden deducir nuevas verdades a partir de axiomas y reglas de inferencia.
- Teoría de conjuntos: estudia las propiedades de los conjuntos, que son colecciones de objetos. Es una de las bases fundamentales de la matemática moderna y tiene aplicaciones en diversas áreas como la topología, el análisis matemático y la teoría de la medida.
- Teoría de la computabilidad: se enfoca en determinar qué problemas pueden resolverse mediante algoritmos computacionales y cuáles no. Al estudiar las capacidades y limitaciones de máquinas abstractas de cómputo, como las máquinas de Turing, esta disciplina aborda cuestiones fundamentales sobre la naturaleza de la computación y la complejidad de los problemas.
- Lógica proposicional: se ocupa del estudio de proposiciones y cómo se combinan mediante conectivos lógicos.
- Lógica de predicados: extiende la lógica proposicional para incluir cuantificadores como "para todo" (∀) y "existe" (∃), permitiendo la expresión de sentencias más complejas que involucran objetos individuales y propiedades.
- Lógica modal: se utiliza para razonar sobre la posibilidad, la necesidad y otros conceptos modales. Introduce operadores modales como "posiblemente" y "necesariamente", permitiendo la expresión de proposiciones que varían según posibles mundos o estados.
Lógica proposicional
La lógica proposicional es una rama de la lógica que se enfoca en el estudio de proposiciones y sus relaciones lógicas. Utiliza conectores y tablas de verdad para analizar y comprender cómo se combinan y relacionan estas proposiciones, lo que nos permite tomar decisiones lógicas y construir argumentos válidos. A continuación, exploraremos los conceptos básicos de la lógica proposicional.
Las proposiciones son afirmaciones o declaraciones que pueden ser verdaderas o falsas, pero no ambas al mismo tiempo. Se las denota con las letras minúsculas p, q, r, s, etc.
Ejemplos:
p: "El cielo es azul"
q: "2 + 2 = 4"
r: "3 es un número par"
Las proposiciones pueden tener dos valores de verdad posibles: verdadero (V) o falso (F). No existe otra posibilidad. El valor de verdad de una proposición p se denota como V(p). En el caso de los ejemplos anteriores:
V(p)=V
V(q)=V
V(r)=F
En lógica matemática existen símbolos que se utilizan para combinar proposiciones y formar nuevas proposiciones, estos se llaman operadores o conectores lógicos. Los más frecuentemente utilizados son:
- Negación (¬): Convierte una proposición verdadera en falsa y viceversa.
- Conjunción (∧): Devuelve verdadera solo si ambas proposiciones son verdaderas.
- Disyunción (∨): Devuelve verdadera si al menos una de las proposiciones es verdadera.
- Implicación (→): Establece una relación de condición, donde si la primera proposición es verdadera, entonces la segunda también lo es.
- Bicondicional (↔): Devuelve verdadera si ambas proposiciones tienen el mismo valor de verdad.
Ejemplos:
p: "El cielo es azul"
q: "2 + 2 = 4"
r: "3 es un número par"
¬p: "El cielo no es azul"
q∧r: "2+2=4 y 3 es un número par"
p∨q: "El cielo es azul o 2+2=4"
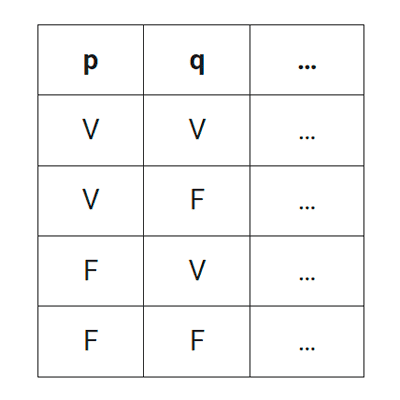
Las proposiciones formadas a partir de otras más simples mediante el uso de conectores lógicos se llaman proposiciones compuestas. Para determinar el valor de verdad de una proposición compuesta tenemos como herramienta a las tablas de verdad. Estas muestran todos los posibles valores de verdad para una proposición dada la verdad o falsedad de sus componentes y los operadores utilizados.
Al confeccionar una tabla de verdad podemos obtener alguno de estos tres casos:
- Tautología: Es una proposición compuesta que siempre es verdadera, sin importar los valores de verdad de sus componentes. Las tautologías también reciben el nombre de leyes lógicas.
- Contingencia: Es una proposición compuesta que puede ser verdadera o falsa dependiendo de los valores de verdad de sus componentes.
- Contradicción: Es una proposición compuesta que siempre es falsa, sin importar los valores de verdad de sus componentes.
Lógica de predicados
La lógica de predicados es una extensión de la lógica proposicional que permite expresar relaciones más complejas y cuantificar sobre objetos y propiedades. Permite crear afirmaciones como "todos los números naturales son positivos" o "existe un número primo mayor que 100".
Los cuantificadores son símbolos que se utilizan para expresar la cantidad de elementos que satisfacen una proposición. Los dos cuantificadores más utilizados son:
- Cuantificador Universal (∀): Se utiliza para decir que una afirmación es verdadera para todos los elementos en un conjunto dado. Por ejemplo, "∀x P(x)" significa que la proposición P(x) es verdadera para todos los valores de x en el conjunto.
- Cuantificador Existencial (∃): Se utiliza para decir que al menos un elemento en un conjunto satisface una proposición. Por ejemplo, "∃x Q(x)" significa que hay al menos un elemento en el conjunto para el cual la proposición Q(x) es verdadera.
Razonamientos
Un razonamiento o argumento es una secuencia de proposiciones que están estructuradas de tal manera que, si las premisas son verdaderas, la conclusión también lo será. Se trata de un proceso en el que se emplean reglas formales para inferir conclusiones a partir de premisas.
Algunos ejemplos de razonamientos son:
- Si llueve, entonces el suelo está mojado; pero el suelo no está mojado. Por lo tanto, no está lloviendo.
- Todos los humanos son mamíferos y todos los mamíferos son vertebrados. Por lo tanto, todo humano es vertebrado.
- Si estudio mucho, entonces aprobaré el examen. Estudié mucho, por tanto, aprobaré el examen.
Las partes de un razonamiento lógico son las siguientes:
- Premisas: son las afirmaciones que se dan como base para la conclusión.
- Conclusión: es la afirmación final a la que se llega a partir de las premisas.
En el ejemplo 1, "si llueve, entonces el suelo está mojado" y "el suelo no está mojado" son las premisas; la conclusión es "no está lloviendo".
Es el tipo de razonamiento más utilizado en lógica matemática es el razonamiento deductivo, donde se parte de premisas conocidas como verdaderas, y mediante reglas lógicas se infiere una conclusión necesaria que sigue lógicamente de esas premisas. Si las premisas son verdaderas y la forma del argumento es válida, entonces la conclusión necesariamente también será verdadera.
Artículos de lógica
Proposiciones lógicas
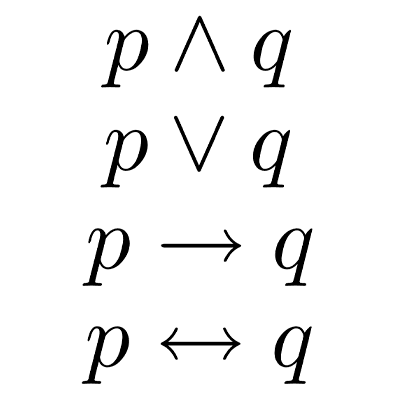
Conectores lógicos
Tablas de verdad
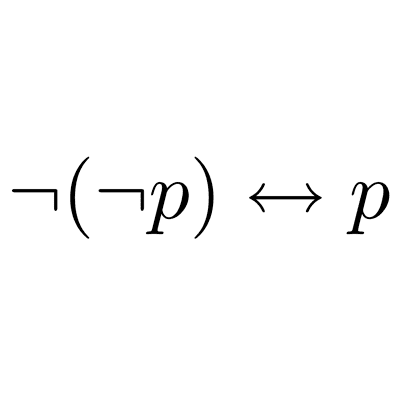
Leyes lógicas
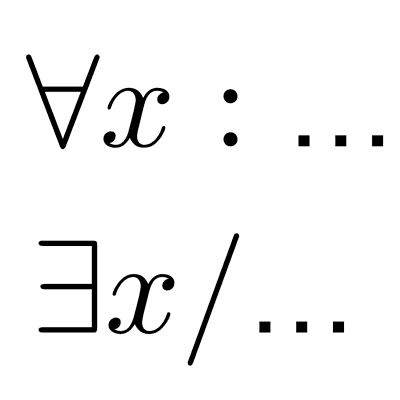
Cuantificadores
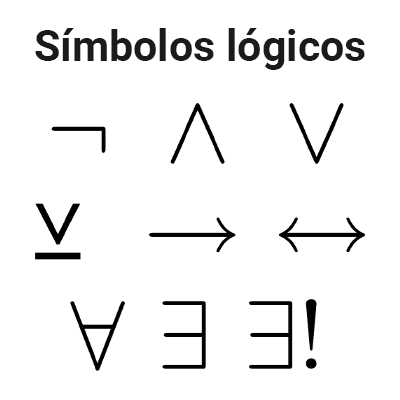
Símbolos lógicos

Contradicción lógica

Tautología lógica

Contingencia lógica

Lógica proposicional

Negación lógica

Conjunción lógica
Bibliografía
- Acevedo González, G. (2011). Lógica Matemática. Universidad Nacional Abierta y a Distancia (UNAD).
- Castillo P, E. y Pinta, M. (2015). Lógica Matemática I: Proposiciones y Leyes de Inferencia (2da edición). Universidad Técnica de Machala.
- Copi, I. y Cohen, C. (2013). Introducción a la Lógica (2da edición). Limusa.
- Corral de Franco, Y. y Manzanares, L. (2018). Nociones Elementales de lógica matemática y teoría de conjuntos. Caracas. Fondo editorial OPSU.
- Daun, J. y Falcón, Y. (1995). Lógica matemática. Universidad Autónoma Metropolitana.
- Garrido, M. (1974). Lógica simbólica (4ta edición). Tecnos.
- Gentile, E. (1984). Notas de Álgebra I. Editorial Universitaria de Buenos Aires.
- Moreno, A. (1969). Lógica matemática: antecedentes y fundamentos. Editorial Universitaria de Buenos Aires.
- Puyau, H. y Roetti, J. (1976). Elementos de Lógica Matemática. Editorial Universitaria de Buenos Aires.
- Rojo, A. (1996). Álgebra I (18a edición). El Ateneo.

Subir
Deja una respuesta