
Conjunción lógica
En este artículo explicamos qué es la conjunción en lógica proposicional, algunos ejemplos de ella, su tabla de verdad, propiedades y aplicaciones, entre otras cosas.
Índice
¿Qué es la conjunción?
La conjunción es un conectivo lógico que une dos proposiciones simples para formar una proposición compuesta. Se representa con el símbolo ∧ que se lee habitualmente como “y”. Una conjunción es verdadera sólo si las proposiciones simples que la componen son verdaderas simultáneamente y es falsa en otros casos.
Algunos ejemplos de conjunción son:
- Si p es “hace frío” y q es “está nevando”, su conjunción es p ∧ q: “hace frío y está nevando”.
- Si p es “4 es un número par” y q es “5 es un número impar”, la conjunción es p ∧ q: “4 es un número par y 5 un número impar”.
- Si r es “Juan estudia mucho” y s es “Juan es buen escritor”, la proposición conjunta r ∧ s es “Juan estudia mucho y es buen escritor”.
Existen diversas formas de leer la proposición p ∧ q:
- p y q.
- p aunque q.
- p pero q.
- p sin embargo q.
- p no obstante q.
- p a pesar de q.
- p además q.
- p mientras q.
A veces también son usados los símbolos “&” o “and”, principalmente en informática. No se debe confundir el símbolo de la conjunción “∧” con el de la disyunción “∨”. Mientras que la conjunción es un “pico” hacia arriba, la disyunción es uno hacia abajo.
Tabla de verdad
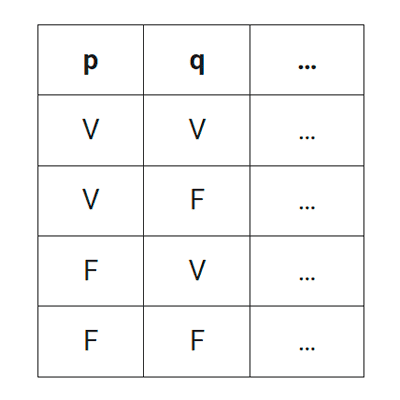
Como se dijo antes, en lógica proposicional la conjunción es verdadera cuando las proposiciones simples que la conforman son verdaderas y es falsa cuando ocurre otro caso, ya sea que una de ellas es falsa o ambas lo son. La tabla de verdad que representa esto es:
| p | q | p ∧ q |
|---|---|---|
| V | V | V |
| V | F | F |
| F | V | F |
| F | F | F |
Por ejemplo, la proposición “hace frío y está nevando” es verdadera sólo cuando es verdadero que hace frío y que está nevando. El enunciado “4 es un número par y 5 un número impar” es verdadero porque es verdadero que 4 es par y 5 es impar. La proposición “un triángulo tiene tres lados y un cuadrado tiene ocho lados” es falsa, porque si bien es cierto que un triángulo tiene tres lados, no es cierto que un cuadrado tenga ocho.
Propiedades de la conjunción
1) Ley conmutativa: el orden de las proposiciones no afecta el resultado.
p ∧ q ≡ q ∧ p
2) Ley asociativa: la agrupación de las proposiciones no afecta el resultado.
p ∧ (q ∧ r) ≡ (p ∧ q) ∧ r
3) Elemento neutro: el elemento neutro de la conjunción es el valor verdadero (V).
p ∧ V ≡ p
4) Elemento absorbente: el elemento absorbente de la conjunción es el valor falso (F).
p ∧ F ≡ F
5) Ley distributiva respecto a la disyunción: la conjunción se distribuye sobre la disyunción y viceversa.
p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)
6) Negación de la conjunción (Ley de De Morgan): la negación de una conjunción se puede expresar en términos de disyunción de las negaciones.
¬(p ∧ q) ≡ ¬p ∨ ¬q
7) Idempotencia: la conjunción de una proposición consigo misma es igual a la proposición original.
p ∧ p ≡ p
8) Eliminación de la conjunción: esta es una regla de inferencia válida que permite afirmar uno de los componentes de una conjunción a partir de la verdad de la conjunción completa. Simbólicamente:
p ∧ q → p
p ∧ q → q
9) La conjunción entre una proposición y su negación es una contradicción, es decir, p ∧ ¬p siempre es falsa.
Conjunción en la teoría de conjuntos
En la teoría de conjuntos, la conjunción lógica se utiliza para definir la intersección de conjuntos, la cual es una operación que consiste en combinar dos conjuntos y formar un nuevo conjunto que contiene sólo los elementos que pertenecen a ambos conjuntos originales.
Definición: si A y B son dos conjuntos, la intersección de A y B, denotada por A ∩ B, se define como el conjunto que contiene todos los elementos que pertenecen a A y a B.
A ∩ B = {x | x ∈ A ∧ x ∈ B}
Nótese la similitud entre el símbolo ∩ y el de la conjunción ∧.
Ejemplos:
- Si A = {1, 2, 3} y B = {2, 3, 4}, entonces A ∩ B = {2, 3}.
- Dados A= {a, b, c, d} y B={d, e, f, g}, entonces A ∩ B = {d}.
- Si A = {rojo, azul, verde} y B = {amarillo, naranja}, entonces A ∩ B = ∅ (conjunto vacío), ya que no hay elementos comunes a ambos conjuntos.
La intersección cumple varias propiedades similares a la conjunción:
- Conmutatividad: A ∩ B = B ∩ A.
- Asociatividad: (A ∩ B) ∩ C = A ∩ (B ∩ C).
- Distributividad sobre la unión: A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C).
- Idempotencia: A ∩ A = A
- Elemento neutro: A ∩ U = A, donde U es el conjunto universal.
- Elemento absorbente: A ∩ ∅ = ∅
- Ley del complemento: A ∩ A’ = ∅
Conjunción en un circuito lógico
La conjunción lógica es un concepto importante en el ámbito de los circuitos digitales y se materializa mediante la puerta AND, un componente electrónico crucial para el funcionamiento de diversos sistemas computacionales. Este concepto proviene del álgebra booleana, una rama de la matemática que se centra en las operaciones lógicas y es fundamental para el diseño de circuitos digitales.
Una puerta AND toma dos o más señales de entrada y produce una salida que es verdadera (1) solo si todas las entradas son verdaderas (1). Si alguna de las entradas es falsa (0), la salida será falsa (0).
Las puertas AND tienen varias aplicaciones en circuitos digitales, incluyendo:
- Implementación de funciones lógicas: las puertas AND se combinan para crear circuitos que realizan diversas funciones lógicas, como comparadores, decodificadores y multiplexores.
- Construcción de unidades aritméticas: las unidades aritméticas básicas, como la suma y la resta, se pueden construir utilizando puertas AND en combinación con otras compuertas lógicas.
- Diseño de sistemas de control: las puertas AND se emplean en sistemas de control para implementar condiciones lógicas que determinan el comportamiento del sistema.
La conjunción lógica se suele representar mediante operadores específicos que varían según el lenguaje de programación. Algunos ejemplos comunes son:
- C/C++: &&
- Java: &&
- Python: and
- JavaScript: &&
Bibliografía
- Acevedo González, G. (2011). Lógica Matemática. Universidad Nacional Abierta y a Distancia (UNAD).
- Castillo P, E. y Pinta, M. (2015). Lógica Matemática I: Proposiciones y Leyes de Inferencia (2da edición). Universidad Técnica de Machala.
- Copi, I. y Cohen, C. (2013). Introducción a la Lógica (2da edición). Limusa.
- Corral de Franco, Y. y Manzanares, L. (2018). Nociones Elementales de lógica matemática y teoría de conjuntos. Caracas. Fondo editorial OPSU.
- Daun, J. y Falcón, Y. (1995). Lógica matemática. Universidad Autónoma Metropolitana.
- Garrido, M. (1974). Lógica simbólica (4ta edición). Tecnos.
- Gentile, E. (1984). Notas de Álgebra I. Editorial Universitaria de Buenos Aires.
- Moreno, A. (1969). Lógica matemática: antecedentes y fundamentos. Editorial Universitaria de Buenos Aires.
- Puyau, H. y Roetti, J. (1976). Elementos de Lógica Matemática. Editorial Universitaria de Buenos Aires.
- Rojo, A. (1996). Álgebra I (18a edición). El Ateneo.

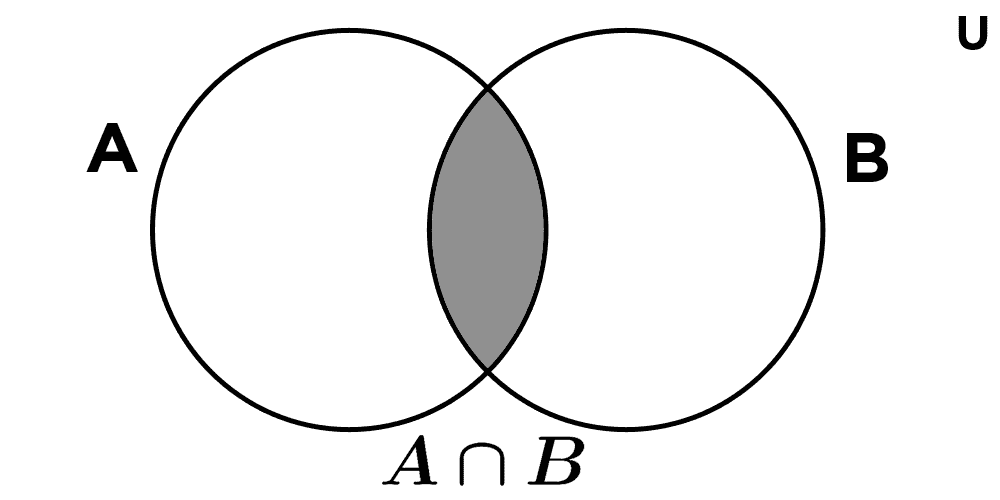

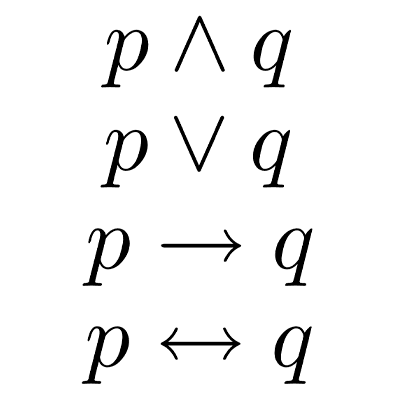
Deja una respuesta