Función lineal

En este artículo explicamos qué son las funciones lineales en matemáticas con ejemplos, gráficas, características, casos especiales y aplicaciones.

¿Qué es una función lineal?

Una función lineal es una relación entre dos variables x e y que puede expresarse de la forma y=mx+b, donde m y b son números reales fijos. Estas funciones se representan gráficamente como líneas rectas, donde el coeficiente m representa la pendiente y el término b representa el punto donde la recta corta al eje y.

Dicho de otro modo, una función lineal es una función algebraica polinómica de primer grado (cuando m no es cero) o grado cero (cuando m es cero). Las partes de la fórmula de una función lineal son: el término lineal mx, donde m es su coeficiente; y el término independiente b.

Aquí hay 10 ejemplos de funciones lineales:

• f(x)=2x+1
• f(x)=-6
• f(x)=-x
• f(x)=-3x-6
• f(x)=3x+1
• f(x)=4-20x+1
• f(x)=5x-14
• f(x)=2x+3x+x
• f(x)=-12x-1
• f(x)=5+6x

Las funciones lineales se utilizan en diversos campos, como la física, la economía, la ingeniería y las ciencias sociales. Se utilizan para modelar relaciones proporcionales entre dos variables, como la distancia recorrida en función del tiempo, el costo total en función de la cantidad comprada o la temperatura en función del tiempo.

Se suele llamar función afín a una de función de la forma f(x)=mx+b, reservando el nombre de "función lineal" para aquella en la que b=0, es decir, f(x)=mx (esta también recibe el nombre de función de proporcionalidad directa). En este artículo trataremos a las funciones lineales y afines como el mismo concepto.

Características y elementos

Una función lineal está compuesta por varios elementos que describen su comportamiento y le dan sus características especiales, estos son:

1. Variables.
2. Dominio.
3. Rango.
4. Gráfica.
5. Pendiente.
6. Ordenada al origen.
7. Raíz.

Variables

Dominio y rango

El dominio de una función es el conjunto de todos los valores posibles que puede tomar la variable independiente. El rango de una función es el conjunto de todos los valores que resultan de aplicar la función a cada número del dominio.

Gráfica

La representación gráfica de una función lineal es una línea recta en un sistema de coordenadas cartesianas. Por este hecho es que se le da el nombre de "lineal".

Si conocemos la ecuación de una función lineal, para representarla gráficamente basta determinar dos de sus puntos y trazar la recta que pasa por ellos. Con el fin de evitar errores, se recomienda hallar varios puntos antes de trazar la recta, de este modo cualquier error de cálculo quedará en evidencia ya que los puntos no están alineados.

Ejemplo: f(x)=2x-3

Hallamos algunos puntos de la gráfica a través de una tabla de valores:

x	y=f(x)	(x, y)
-2	2(-2)-3= -7	(-2, -7)
-1	2(-1)-3= -5	(-1, -5)
0	2(0)-3= -3	(0, -3)
1	2(1)-3= -1	(1, -1)
2	2(2)-3= 1	(2, 1)

En la última columna vemos los puntos que debemos ubicar en un plano cartesiano:

Habiendo confirmado que los puntos están alineados, procedemos a trazar la recta que pasa por ellos y escribir la fórmula de la función que estamos representando. Con ello nuestro trabajo está concluido.

Tres métodos para graficar una función lineal (con ejemplos)

Pendiente

La pendiente de una función lineal es el coeficiente del término lineal, o sea, el número m. Este valor indica la inclinación de la recta que representa la función en un sistema de coordenadas cartesianas.

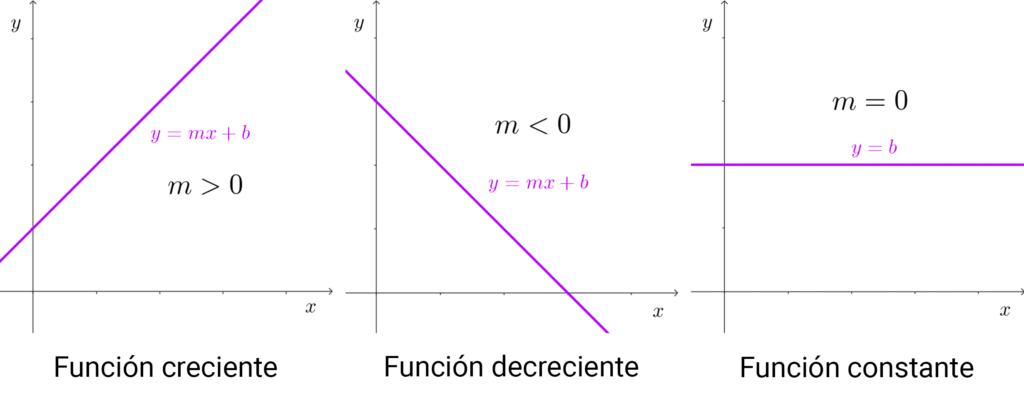
La pendiente también determina si la función lineal es creciente o decreciente: si es positiva, entonces la función es creciente; si es negativa, la función es decreciente. Cuando la pendiente es cero, la función no es creciente ni decreciente, sino que es constante.

En el siguiente gráfico vemos cómo afecta el signo de la pendiente a la gráfica:

Cuando tenemos la ecuación de una función lineal, hallar la pendiente consiste en encontrar el valor que multiplica a la x (la variable independiente). Si en la ecuación no aparece la x, significa que la pendiente es cero.

Ejemplos:

• La función y=2x+1 tiene pendiente 2; como es un número positivo, la función es creciente.
• f(x)=-6 tiene pendiente 0, pues no se ve la variable independiente en la ecuación. Por esto mismo, la función es constante.
• g(x)=-x-1 tiene pendiente -1; por ser un número negativo, la función lineal de decreciente.

También se puede hallar la pendiente de una función lineal a partir de su gráfica. Para esto, utilizamos la siguiente propiedad.

Ejemplo:

Queremos determinar la pendiente de una función lineal que pasa por los puntos (-2, -7) y (-1, -5). Para esto, calculamos las variaciones:

*Δy=y_2-y_1=-5-(-7)=2*

*Δx=x_2-x_1=-1-(-2)=1*

Teniendo estos números hallamos el cociente: *\dfrac{Δy}{Δx}=\dfrac{2}{1}=2*

Entonces, la pendiente que buscábamos es m=2.

Ordenada al origen

La ordenada al origen de una función lineal es el valor de su término independiente. Gráficamente, representa el punto en el cual la gráfica corta al eje y (cuando x es igual a cero).

Para hallar la ordenada al origen, basta con encontrar el término en la ecuación que no tiene x. Una función lineal siempre tiene ordenada al origen. Si esta no se ve en la ecuación, es porque es igual a cero.

Ejemplos

• La función y=2x+1 tiene ordenada al origen 1.
• f(x)=-6 tiene ordenada al origen -6.
• g(x)=-x-1 tiene ordenada al origen -1.
• h(x)=2x tiene ordenada al origen igual a 0.

Para hallar gráficamente la ordenada al origen, es necesario encontrar el punto donde la recta corta al eje vertical. Nótese que si en una función f(x)=mx+b hacemos x=0, ocurre que

*f(0)=m(0)+b→f(0)=b.*

Entonces, la gráfica de una función lineal corta al eje y en el punto (0,b), siendo b la ordenada al origen.

Por ejemplo, la gráfica de la siguiente función corta al eje vertical en 1, este valor es su ordenada al origen. Este dato coincide con el que obtendríamos si miramos la ecuación.

Raíz

La raíz o cero de una función lineal es la coordenada x del punto donde la gráfica corta al eje x.

Para calcular la raíz de la función, se iguala la ecuación a 0 y se despeja x:

*mx+b=0→x=-\dfrac{b}{m}*

Entonces, la gráfica corta al eje x en el punto (-b/m,0), siendo la raíz de la función el valor *x=-\dfrac{b}{m}.* No es necesario memorizar esta fórmula, es suficiente con conocer el procedimiento de igualar a cero y luego despejar.

Ejemplo:

Para hallar la raíz de f(x)=2x+1, igualamos la ecuación cero y despejamos x:

*2x+1=0*

*2x=-1*

*x=-\dfrac{1}{2}*

Entonces, la raíz de la función es *x=-\dfrac{1}{2},* con lo cual la gráfica corta al eje x en el punto (-1/2, 0). Se puede comprobar que el cálculo es correcto mirando la gráfica anterior (-1/2 es -0,5 en escritura decimal).

Casos especiales

Además del caso general, existen dos tipos especiales de funciones lineales que se dan cuando la pendiente y la ordenada al origen toman ciertos valores. Veremos ambos a continuación.

Función constante

La función constante se da cuando la pendiente es cero (m=0). La ecuación tiene la forma f(x)=b y su gráfica es una línea horizontal. La ordenada al origen es b y la función no tiene raíz (salvo cuando b=0).

Ejemplo: f(x)=3

Función identidad

La función identidad se da cuando la pendiente es 1 (m=1) y la ordenada al origen es cero (b=0). Su ecuación es f(x)=x, y la gráfica es una recta que pasa por el origen con un ángulo de 45° respecto al eje x.

Aplicaciones de las funciones lineales

Las funciones lineales son de las más simples que podemos estudiar y tienen aplicaciones en diversos campos. A continuación veremos dos ejemplos de aplicación a la economía.

Funciones de costo

Los taxis de una localidad cobran $5 por la bajada de bandera y $2 por cada kilómetro recorrido. Se pide:

1. Encontrar una función que permita calcular el costo del viaje cualquiera sea la distancia recorrida.
2. Calcular el costo de recorrer 2km; 5,6km y 200km.

1) Sabemos que la bajada de bandera es un costo fijo que se paga por empezar un viaje, entonces siempre estará sumándose al costo final. Luego, si x es la cantidad de kilómetros recorridos, el costo por ellos será de 2x. El costo por el viaje será entonces 2x+5, la cual es una función lineal que podemos escribir de la siguiente forma:

C(x)=2x+5

2) Para cualquier x (cantidad de kilómetros recorridos) podemos calcular el costo del taxi mediante la fórmula anterior.

Si x=2→C(2)=2\cdot(2)+5=9, entonces, un viaje de 2 km cuesta $9.

Si x=5,6→C(5,6)=2\cdot(5,6)+5=16,2,, entonces, un viaje de 5,6 km cuesta $16,2.

Si x=200→C(200)=2\cdot(200)+5=405, entonces, un viaje de 200 km cuesta $405.

Cálculo de interés simple

El interés simple es un método de calcular el interés sobre un préstamo o inversión en el que se aplica un porcentaje fijo al monto inicial durante un período de tiempo específico. En el interés simple, el interés se calcula únicamente sobre el monto original sin considerar los intereses generados anteriormente.

El interés simple es directamente proporcional al monto principal, a la tasa de interés y al tiempo. A medida que cualquiera de estos elementos aumenta, el interés total también aumenta linealmente.

Si se dejan fijas dos de las variables, por ejemplo, el capital inicial y la tasa de interés, el interés se convierte en una función lineal que depende de la cantidad de tiempo (en períodos):

*I(t)=C\cdot i\cdot t*

Ejemplo: Dado un capital inicial de $100 y una tasa de interés del 2% mensual (0,02 en decimal), el interés generado en t meses es:

*I(t)=(100)\cdot (0,02)\cdot t=2t*

Esta es una función lineal con variable independiente t y variable dependiente I. Nos permite conocer el interés en función de la cantidad de meses transcurridos:

• Luego de 3 meses, el interés generado es: *I(3)=2\cdot 3=6,* o sea, $6.
• Luego de 18 meses, el interés es: *I(18)=2\cdot 18=36,* o sea, $36.
• Luego de 24 meses, el interés generado es: *I(24)=2\cdot 24=48,* o sea, $48.

Ejercicios para practicar

Preguntas frecuentes

¡Continúa leyendo estos artículos relacionados!

Infografías