Cómo graficar funciones lineales
En este artículo veremos cómo graficar funciones lineales mediante tres métodos con ejemplos explicados de cada uno.
Índice
Primera forma: usando tabla de valores
Este método consiste en hallar las imágenes de algunos valores del dominio para luego ubicar los puntos de la función en el plano cartesiano.
Pasos para hallar la gráfica de una función lineal usando tabla de valores
- Construir una tabla seleccionado algunos valores del dominio, sus imágenes y el punto correspondiente que se forma.
- Ubicar todos los puntos en el plano cartesiano. Estos deben quedar alineados.
- Trazar la recta que une todos los puntos y escribir la ecuación de la función.
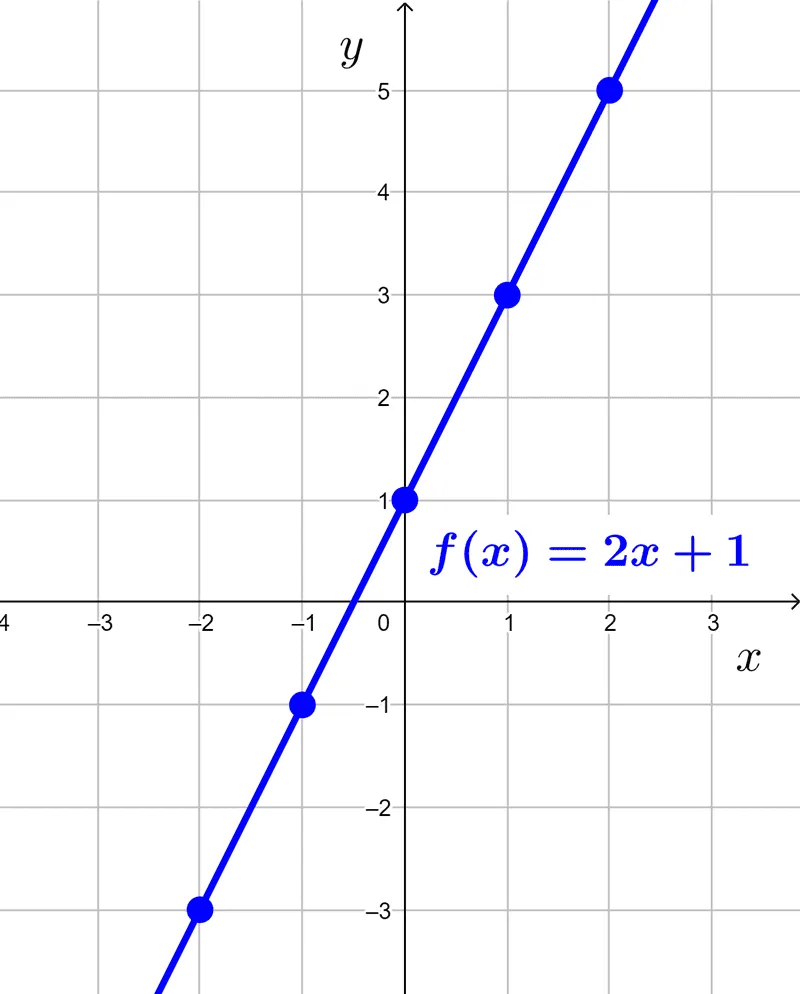
Ejemplo: *f(x)=2x+1*
Construimos una tabla como la siguiente:
- En la primera columna seleccionaremos valores *x* que están en el dominio de la función. Es conveniente usar números no muy lejanos del cero para que a la hora de graficar no se complique.
- En la segunda columna irán las imágenes de los números anteriores.
- En la tercera irá el par ordenado formado por los números anteriores. Este corresponde al punto que ubicaremos en el plano.
| *x* | *y=f(x)* | *(x, y)* |
| *-2* | *f(-2)=2(-2)+1=-3* | *(-2, -3)* |
| *-1* | *f(-1)=2(-1)+1=-1* | *(-1, -1)* |
| *0* | *f(0)=2(0)+1=1* | *(0, 1)* |
| *1* | *f(1)=2(1)+1=3* | *(1, 3)* |
| *2* | *f(2)=2(2)+1=5* | *(2, 5)* |
Los puntos de la última columna los ubicamos en un plano cartesiano. Puede verse que estos están alineados, lo cual es de esperarse porque la gráfica de la función es una recta.
Por último, trazamos la recta que pasa por todos los puntos y escribimos el nombre de la función.
La razón de hallar varios puntos en la tabla y no solo dos (que bastarían para hallar la gráfica en este caso) es que, si se cometieron errores en el cálculo, esto será evidente al plasmar los puntos en el plano, ya que no estarán alineados como deberían.
Segunda forma: usando raíz y ordenada al origen
Este método es similar al anterior, solo que esta vez usaremos solo dos puntos. Estos no son al azar, sino que son los puntos de corte con cada eje: la raíz y la ordenada al origen.
Recordemos que dada una función lineal *f(x)=mx+b,* su raíz es el punto donde vale cero, es decir, el valor de *x* que cumple *mx+b=0.* La ordenada al origen es la imagen del *0,* es decir, el número *f(0)=b.*
Hallando estos dos puntos y ubicándolos en el plano, podremos trazar la recta que pasa por ellos, siendo esta la gráfica de la función.
Pasos para hallar la gráfica de una función usando su raíz y ordenada al origen
- Hallar la raíz igualando la ecuación de la función a cero.
- Hallar la ordenada al origen, la cual se extrae rápidamente desde la fórmula.
- Ubicar ambos puntos en el plano cartesiano, sobre su eje correspondiente (la raíz sobre el eje x y la ordenada al origen sobre el eje y).
- Trazar la recta que une ambos puntos y escribir la ecuación de la función.
Ejemplo: *f(x)=-3x-6*
Calculamos la raíz:
*-3x-6=0*
*-3x=6*
*x=\dfrac{6}{-3}=-2*
Calculamos la ordenada al origen, que no es otra cosa que el término que no tiene *x,* en este caso, *-6.*
Ahora ubicamos ambos puntos, la raíz sobre el eje x y la ordenada al origen sobre el eje y.
Para finalizar trazamos la recta que une los puntos y escribimos la fórmula de la función.
Tercera forma: usando la pendiente y ordenada al origen
Recordemos que en una función lineal *f(x)=mx+b* la pendiente es el número *m,* el cual mide la inclinación de la recta.
La pendiente es la razón entre la variación vertical y la horizontal (véase qué es una función lineal):
Podemos hallar la gráfica sabiendo esta información, que extraemos de la misma ecuación. Será necesario un punto, desde el cual mediremos las variaciones. Usaremos la ordenada al origen, ya que esta también puede leerse de la ecuación.
Pasos para hallar la gráfica de una función lineal usando su pendiente y ordenada al origen
- Ubicar la ordenada al origen en el plano cartesiano.
- Desplazarse horizontalmente hacia la derecha las unidades que figuran en el denominador de la pendiente.
- A partir del último punto, si la pendiente es positiva, desplazarse verticalmente hacia arriba las unidades que figuran en el numerador de la pendiente. Si ésta es negativa, realizar el desplazamiento hacia abajo.
- Trazar la recta que une la ordenada al origen con el último punto hallado. Esta es la gráfica de la función.
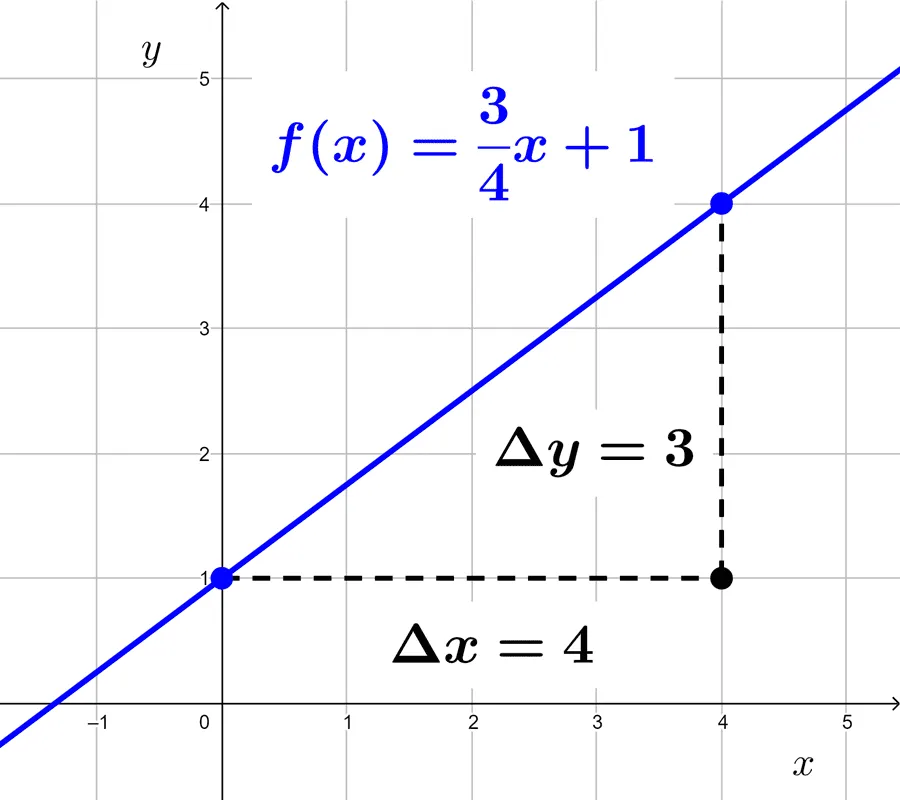
Ejemplo 1 (pendiente positiva): *f(x)=\dfrac{3}{4}x+1*
Extraemos la pendiente: *\dfrac{3}{4}.* Este número significa que por cada *3* unidades que nos desplacemos verticalmente, debemos desplazarnos *4* horizontalmente:
*Δy=3* (desplazamiento vertical)
*Δx=4* (desplazamiento horizontal)
Lo primero que hacemos es, en un plano cartesiano, ubicar la ordenada al origen, que es *1.* Luego, a partir de ese punto nos desplazamos horizontalmente hacia la derecha las unidades que se nos pide, *4*.
A partir del nuevo punto, nos desplazamos verticalmente hacia arriba las unidades solicitadas: *3.*
Este último punto hallado pertenece a la gráfica que buscamos. Terminamos trazando la recta que une este punto con la ordenada al origen y escribiendo la ecuación de la función.
Podemos borrar los segmentos auxiliares que utilizamos y dejar solo la recta.
Ejemplo 2 (pendiente negativa): *f(x)=-\dfrac{2}{5}x+2*
En este caso, la pendiente *-\dfrac{2}{5}* es negativa. Esto solo indica que el desplazamiento vertical debemos hacerlo hacia abajo en lugar de hacia arriba. Todo lo demás se mantiene.
*Δy=-2* (desplazamiento vertical)
*Δx=5* (desplazamiento horizontal)
Ubicamos la ordenada al origen y nos desplazamos *5* unidades de forma horizontal hacia la derecha. Luego, a partir de ese punto nos desplazamos verticalmente hacia abajo *2* unidades.
Para finalizar, trazamos la recta que une el último punto con la ordenada al origen y escribimos la ecuación de la función.
Nota: En el caso de que la pendiente sea un número entero, por ejemplo en *f(x)=2x+1,* esta se entiende como el número fraccionario *\dfrac{2}{1},* de modo que el desplazamiento vertical será de *2* y el horizontal de *1.*
*Δy=2*
*Δx=1*
Subir
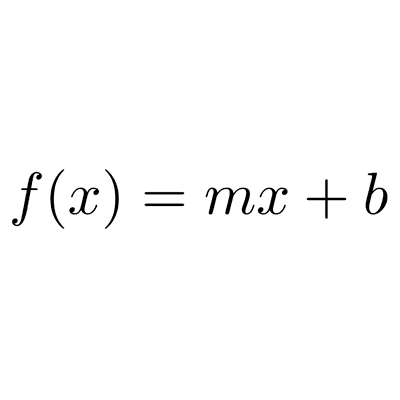
Deja una respuesta